变分自编码器(四):一步到位的聚类方案
By 苏剑林 | 2018-09-17 | 485250位读者 |由于VAE中既有编码器又有解码器(生成器),同时隐变量分布又被近似编码为标准正态分布,因此VAE既是一个生成模型,又是一个特征提取器。在图像领域中,由于VAE生成的图片偏模糊,因此大家通常更关心VAE作为图像特征提取器的作用。提取特征都是为了下一步的任务准备的,而下一步的任务可能有很多,比如分类、聚类等。本文来关心“聚类”这个任务。
一般来说,用AE或者VAE做聚类都是分步来进行的,即先训练一个普通的VAE,然后得到原始数据的隐变量,接着对隐变量做一个K-Means或GMM之类的。但是这样的思路的整体感显然不够,而且聚类方法的选择也让我们纠结。本文介绍基于VAE的一个“一步到位”的聚类思路,它同时允许我们完成无监督地完成聚类和条件生成。
理论 #
一般框架 #
回顾VAE的loss(如果没印象请参考《变分自编码器(二):从贝叶斯观点出发》):
$$KL\Big(p(x,z)\Big\Vert q(x,z)\Big) = \iint p(z|x)\tilde{p}(x)\ln \frac{p(z|x)\tilde{p}(x)}{q(x|z)q(z)} dzdx\tag{1}$$
通常来说,我们会假设$q(z)$是标准正态分布,$p(z|x),q(x|z)$是条件正态分布,然后代入计算,就得到了普通的VAE的loss。
然而,也没有谁规定隐变量一定是连续变量吧?这里我们就将隐变量定为$(z, y)$,其中$z$是一个连续变量,代表编码向量;$y$是离散的变量,代表类别。直接把$(1)$中的$z$替换为$(z,y)$,就得到
$$KL\Big(p(x,z,y)\Big\Vert q(x,z,y)\Big) = \sum_y \iint p(z,y|x)\tilde{p}(x)\ln \frac{p(z,y|x)\tilde{p}(x)}{q(x|z,y)q(z,y)} dzdx\tag{2}$$
这就是用来做聚类的VAE的loss了。
分步假设 #
啥?就完事了?呃,是的,如果只考虑一般化的框架,$(2)$确实就完事了。
不过落实到实践中,$(2)$可以有很多不同的实践方案,这里介绍比较简单的一种。首先我们要明确,在$(2)$中,我们只知道$\tilde{p}(x)$(通过一批数据给出的经验分布),其他都是没有明确下来的。于是为了求解$(2)$,我们需要设定一些形式。一种选取方案为
$$p(z,y|x)=p(y|z)p(z|x),\quad q(x|z,y)=q(x|z),\quad q(z,y)=q(z|y)q(y)\tag{3}$$
代入$(2)$得到
$$KL\Big(p(x,z,y)\Big\Vert q(x,z,y)\Big) = \sum_y \iint p(y|z)p(z|x)\tilde{p}(x)\ln \frac{p(y|z)p(z|x)\tilde{p}(x)}{q(x|z)q(z|y)q(y)} dzdx\tag{4}$$
其实$(4)$式还是相当直观的,它分布描述了编码和生成过程:
1、从原始数据中采样到$x$,然后通过$p(z|x)$可以得到编码特征$z$,然后通过分类器$p(y|z)$对编码特征进行分类,从而得到类别;
2、从分布$q(y)$中选取一个类别$y$,然后从分布$q(z|y)$中选取一个随机隐变量$z$,然后通过生成器$q(x|z)$解码为原始样本。
具体模型 #
$(4)$式其实已经很具体了,我们只需要沿用以往VAE的做法:$p(z|x)$一般假设为均值为$\mu(x)$方差为$\sigma^2(x)$的正态分布,$q(x|z)$一般假设为均值为$G(z)$方差为常数的正态分布(等价于用MSE作为loss),$q(z|y)$可以假设为均值为$\mu_y$方差为1的正态分布,至于剩下的$q(y),p(y|z)$,$q(y)$可以假设为均匀分布(它就是个常数),也就是希望每个类大致均衡,而$p(y|z)$是对隐变量的分类器,随便用个softmax的网络就可以拟合了。
最后,可以形象地将$(4)$改写为
$$\mathbb{E}_{x\sim\tilde{p}(x)}\Big[-\log q(x|z) + \sum_y p(y|z) \log \frac{p(z|x)}{q(z|y)} + KL\big(p(y|z)\big\Vert q(y)\big)\Big],\quad z\sim p(z|x) \tag{5}$$
其中$z\sim p(z|x)$是重参数操作,而方括号中的三项loss,各有各的含义:
1、$-\log q(x|z)$希望重构误差越小越好,也就是$z$尽量保留完整的信息;
2、$\sum_y p(y|z) \log \frac{p(z|x)}{q(z|y)}$希望$z$能尽量对齐某个类别的“专属”的正态分布,就是这一步起到聚类的作用;
3、$KL\big(p(y|z)\big\Vert q(y)\big)$希望每个类的分布尽量均衡,不会发生两个几乎重合的情况(坍缩为一个类)。当然,有时候可能不需要这个先验要求,那就可以去掉这一项。
实验 #
实验代码自然是Keras完成的了(^_^),在mnist和fashion-mnist上做了实验,表现都还可以。实验环境:Keras 2.2 + tensorflow 1.8 + Python 2.7。
代码实现 #
代码位于:https://github.com/bojone/vae/blob/master/vae_keras_cluster.py
其实注释应该比较清楚了,而且相比普通的VAE改动不大。可能稍微有难度的是$\sum_y p(y|z) \log \frac{p(z|x)}{q(z|y)}$这个怎么实现。首先我们代入
$$\begin{aligned}p(z|x)&=\frac{1}{\prod\limits_{i=1}^d\sqrt{2\pi\sigma_i^2(x)}}\exp\left\{-\frac{1}{2}\left\Vert\frac{z - \mu(x)}{\sigma(x)}\right\Vert^2\right\}\\
q(z|y)&=\frac{1}{(2\pi)^{d/2}}\exp\left\{-\frac{1}{2}\left\Vert z - \mu_y\right\Vert^2\right\}\end{aligned}\tag{6}$$
得到
$$\log \frac{p(z|x)}{q(z|y)}=-\frac{1}{2}\sum_{i=1}^d \log \sigma_i^2(x)-\frac{1}{2}\left\Vert\frac{z - \mu(x)}{\sigma(x)}\right\Vert^2 + \frac{1}{2}\left\Vert z - \mu_y\right\Vert^2 \tag{7}$$
注意其实第二项是多余的,因为重参数操作告诉我们$z = \varepsilon\otimes \sigma(x) + \mu(x),\,\varepsilon\sim \mathcal{N}(0,1)$,所以第二项实际上只是$-\Vert \varepsilon\Vert^2/2$,跟参数无关,所以$$\log \frac{p(z|x)}{q(z|y)}\sim -\frac{1}{2}\sum_{i=1}^d \log \sigma_i^2(x) + \frac{1}{2}\left\Vert z - \mu_y\right\Vert^2 \tag{8}$$
然后因为$y$是离散的,所以事实上$\sum_y p(y|z) \log \frac{p(z|x)}{q(z|y)}$就是一个矩阵乘法(相乘然后对某个公共变量求和,就是矩阵乘法的一般形式),用K.batch_dot实现。
其他的话,读者应该清楚普通的VAE的实现过程,然后才看本文的内容和代码,不然估计是一脸懵的。
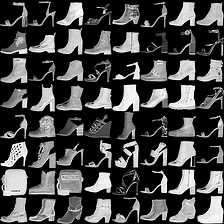
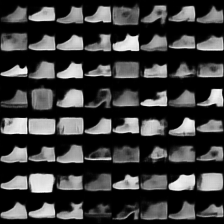
mnist #
这里是mnist的实验结果图示,包括类内样本图示和按类采样图示。最后还简单估算了一下,以每一类对应的数目最多的那个真实标签为类标签的话,最终的test准确率大约有83%,对比这篇文章《Unsupervised Deep Embedding for Clustering Analysis》的结果(最高也是84%左右),感觉应该很不错了。
聚类图示 #
按类采样 #
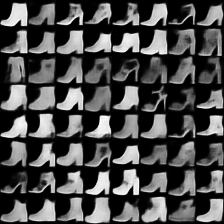
fashion-mnist #
这里是fashion-mnist的实验结果图示,包括类内样本图示和按类采样图示,最终的test准确率大约有58.5%。
聚类图示 #
按类采样 #
总结 #
文章简单地实现了一下基于VAE的聚类算法,算法的特点就是一步到位,结合“编码”、“聚类”和“生成”三个任务同时完成,思想是对VAE的loss的一般化。
感觉还有一定的提升空间,比如式$(4)$只是式$(2)$的一个例子,还可以考虑更加一般的情况。代码中的encoder和decoder也都没有经过仔细调优,仅仅是验证想法所用。
转载到请包括本文地址:https://kexue.fm/archives/5887
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Sep. 17, 2018). 《变分自编码器(四):一步到位的聚类方案 》[Blog post]. Retrieved from https://kexue.fm/archives/5887
@online{kexuefm-5887,
title={变分自编码器(四):一步到位的聚类方案},
author={苏剑林},
year={2018},
month={Sep},
url={\url{https://kexue.fm/archives/5887}},
}








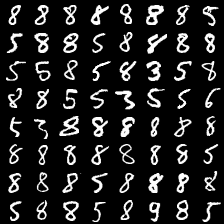
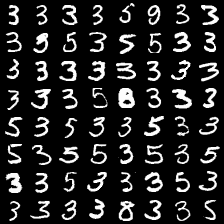
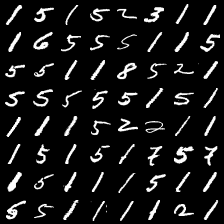
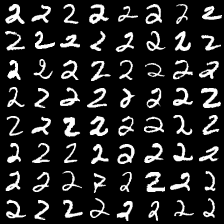
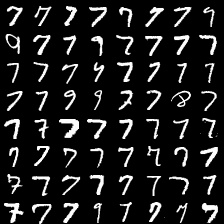
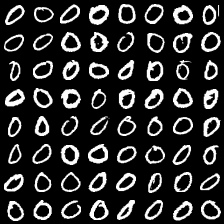
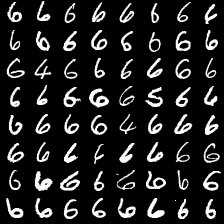

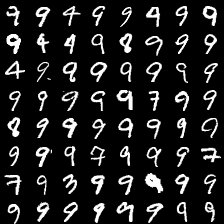




























January 31st, 2021
苏老师,又来麻烦您,请教您一个问题。
我参照您的那个基于多层感知机(MLP)的代码(vae_keras.py)以及您发的这篇文章对应的代码(vae_keras_cluster.py),修改成一个基于MLP的VAE聚类。我在您代码的编码和解码部分都加了一个Dense层,就像下面这样
x = Input(shape=(original_dim,))
h = Dense(intermediate_dim, activation='relu')(x)
#加一层
h = Dense(intermediate_dim, activation='relu')(h)
发现聚类准确率有71%。
请问您
1. Dense层的输入输出节点数是否要修改,比如您这里第一个Dense层输入original_dim,输出intermediate_dim。我是不是要选择比intermediate_dim更多的节点数。我新加的Dense层也是这个问题。
2. 我是否还需要增加更多的Dense层以此提高聚类效果。还有是不是还需要dropout?
麻烦您了,谢谢您
我在编码解码位置都增加2个dense层,
#加2层
h = Dense(intermediate_dim, activation='relu')(h)
h = Dense(intermediate_dim, activation='relu')(h)
发现聚类准确率有78%
如果增加3个Dense层,
#加3层
h = Dense(intermediate_dim, activation='relu')(h)
h = Dense(intermediate_dim, activation='relu')(h)
h = Dense(intermediate_dim, activation='relu')(h)
聚类准确率下降到69%。
请问您对层数选择以及相关参数选择,有没有什么依据,谢谢您。
能跑通代码,那我的事情已经完成了。对于炼丹过程,我不提供参考意见。
February 12th, 2021
祝福苏老师新年平安健康喜乐如意! Happy 牛 Year!
谢谢!同祝同乐~
April 26th, 2021
苏老师您好,请问一下latent_dim的选取有什么规则吗?
June 17th, 2021
苏老师,想问一下从隐藏变量latent feature中提取的可以直接用来表示原始数据吗?原有数据标签还有意义吗?可以照常使用吗?
这不就取决于重构loss的大小吗?重构loss足够小,那么隐变量就相当于原始数据。
苏老师,这个重构loss我能理解,主要是不太知道那个隐变量好像有一个随机采样,那采样前后和能直接用原始数据的标签吗?不用隐变量解码数据而是直接用隐变量画图。
感谢苏老师的解答!
你要分析采样前后的变量,那就要用到概率分布的语言,而不是单纯地“拍板”能还是不能。
好的!了解了,谢谢苏老师!
July 1st, 2021
有一个问题,文章说生成过程:从分布$q(y)$中选取一个类别$y$,然后从分布$q(z|y)$中选取一个随机隐变量$z$,然后通过生成器$q(x|z)$解码为原始样本。
但是代码中,生成过程是:
z = Lambda(sampling, output_shape=(latent_dim,))([z_mean, z_log_var])
x_recon = decoder(z)
这里的解码器的$z$直接用了编码器重采样的结果,不是应该有一个从$y$到$z$的过程再输入解码器?
这说的是随机采样过程,不是训练过程,训练过程不是随机采样,训练过程请认真理解$(5)$式。
November 29th, 2021
苏老师,这儿有点困惑 cat_loss = K.mean(y * K.log(y + K.epsilon()), 0) 分类损失怎么自己跟自己的交叉熵?
一切按照公式实现。
我和你有一样的问题 请问解决了吗
November 29th, 2021
哦,好像想明白了,是信息熵越小,分类越确定吧。
September 16th, 2022
很感谢您的文章。写得非常清楚,但是我还是有点不太明白,所以想请问一下:
1、文章中提到【∑yp(y|z)logp(z|x)q(z|y)希望z能尽量对齐某个类别的“专属”的正态分布。】为什么这个loss有这个效果呢,如何去理解。
2、文章中提到【KL(p(y|z)‖‖q(y))希望每个类的分布尽量均衡,不会发生两个几乎重合的情况(坍缩为一个类)。】 这一项loss是希望p(y|z)接近均匀分布q(y), 也就是z和y无关。因为聚类是希望建立起z和y的关系,这一项loss是不是和聚类目标冲突呢?
1、最后化简我们得到$(8)$,从它的形式可以看出它希望$z$向某个$\mu_y$看齐;或者我们也可以不严谨地将它看成
$$\sum_y p(y|z) KL(p(z|x)\Vert q(z|y))$$
这也显示出它希望$p(z|x)$跟某个$q(z|y)$接近(这样loss才能尽量接近于0)
2、所有loss是一同优化的,拆开来看只是为了分析它的大致优化方向,并不是说其他项loss就不存在了,所以有其他loss存在,就不存在冲突的说法。
December 25th, 2022
拜读了苏神的VAE系里文章,受益匪浅。只是对于这个地方有一些疑惑。
按照我的理解,加上隐含变量$z$后,这一项应该为
\[
\mathbb{E}_{x\sim \tilde{p}(x)}\left[\sum_{y} \int_z p(y|z)p(z|x) \ln\left(\frac{p(z|x)}{q(z|y)} \right) dz \right]
\]
注意到$p(y|z)$中含有变量$z$,所以积分$\int_z $应该不能移到$p(y|z)$后面,所以应该不能得到$KL(p(z|x) || q(z|y))$。
还望苏神能解答上面疑惑。
我看了看正文,似乎没出现过$KL(p(z|x)\Vert q(z|y))$。你是不是指@苏剑林|comment-19844这里的评论?这里确实有些不严谨,我修改一下。
August 23rd, 2023
苏老师,您好,看了您的代码和文章有个问题很想问您:
1、文中公式(8)中1/2*||z−μy||^2,这一项按理说不应该是z的每个样本去减专属于这个样本所对应的类的均值μy吗?
2、但是在代码里我看到的是“z - K.expand_dims(self.mean, 0)”,这里z的shape是(batch_size, 1, latent_dim),self.mean的shape是(1, num_classes, latent_dim),类似于pytorch的广播机制,z会复制变成shape是(batch_size,num_classes, latent_dim),self.mean同理也是,再进行相减。这样相减出来的张量表示的意思岂不是,表示每个样本与每个类别的均值之间的差吗??这和公式(8)的意思不是不一致吗?而且我不知道求一个样本和不属于这个样本的类的均值之间作差有什么意义?
希望苏老师能解答一下我的疑惑,不甚感激。
还是说一切按照公式执行
这是个聚类方案,不存在事先指定的每个样本的专属类别。公式$(8)$的意思就是样本$z$减去类别$y$的均值,然后代入到$(5)$就是每一项还要再乘以$p(y|z)$然后求和。