细水长flow之NICE:流模型的基本概念与实现
By 苏剑林 | 2018-08-11 | 402905位读者 |前言:自从在机器之心上看到了glow模型之后(请看《下一个GAN?OpenAI提出可逆生成模型Glow》),我就一直对其念念不忘。现在机器学习模型层出不穷,我也经常关注一些新模型动态,但很少像glow模型那样让我怦然心动,有种“就是它了”的感觉。更意外的是,这个效果看起来如此好的模型,居然是我以前完全没有听说过的。于是我翻来覆去阅读了好几天,越读越觉得有意思,感觉通过它能将我之前的很多想法都关联起来。在此,先来个阶段总结。
背景 #
本文主要是《NICE: Non-linear Independent Components Estimation》一文的介绍和实现。这篇文章也是glow这个模型的基础文章之一,可以说它就是glow的奠基石。
艰难的分布 #
众所周知,目前主流的生成模型包括VAE和GAN,但事实上除了这两个之外,还有基于flow的模型(flow可以直接翻译为“流”,它的概念我们后面再介绍)。事实上flow的历史和VAE、GAN它们一样悠久,但是flow却鲜为人知。在我看来,大概原因是flow找不到像GAN一样的诸如“造假者-鉴别者”的直观解释吧,因为flow整体偏数学化,加上早期效果没有特别好但计算量又特别大,所以很难让人提起兴趣来。不过现在看来,OpenAI的这个好得让人惊叹的、基于flow的glow模型,估计会让更多的人投入到flow模型的改进中。
生成模型的本质,就是希望用一个我们知道的概率模型来拟合所给的数据样本,也就是说,我们得写出一个带参数$\boldsymbol{\theta}$的分布$q_{\boldsymbol{\theta}}(\boldsymbol{x})$。然而,我们的神经网络只是“万能函数拟合器”,却不是“万能分布拟合器”,也就是它原则上能拟合任意函数,但不能随意拟合一个概率分布,因为概率分布有“非负”和“归一化”的要求。这样一来,我们能直接写出来的只有离散型的分布,或者是连续型的高斯分布。
当然,从最严格的角度来看,图像应该是一个离散的分布,因为它是由有限个像素组成的,而每个像素的取值也是离散的、有限的,因此可以通过离散分布来描述。这个思路的成果就是PixelRNN一类的模型了,我们称之为“自回归流”,其特点就是无法并行,所以计算量特别大。所以,我们更希望用连续分布来描述图像。当然,图像只是一个场景,其他场景下我们也有很多连续型的数据,所以连续型的分布的研究是很有必要的。
各显神通 #
所以问题就来了,对于连续型的,我们也就只能写出高斯分布了,而且很多时候为了方便处理,我们只能写出各分量独立的高斯分布,这显然只是众多连续分布中极小的一部分,显然是不够用的。为了解决这个困境,我们通过积分来创造更多的分布:
$$q(\boldsymbol{x})=\int q(\boldsymbol{z})q_{\boldsymbol{\theta}}(\boldsymbol{x}|\boldsymbol{z}) d\boldsymbol{z}\tag{1}$$
这里$q(\boldsymbol{z})$一般是标准的高斯分布,而$q_{\boldsymbol{\theta}}(\boldsymbol{x}|\boldsymbol{z})$可以选择任意的条件高斯分布或者狄拉克分布。这样的积分形式可以形成很多复杂的分布。理论上来讲,它能拟合任意分布。
现在分布形式有了,我们需要求出参数$\boldsymbol{\theta}$,那一般就是最大似然,假设真实数据分布为$\tilde{p}(\boldsymbol{x})$,那么我们就需要最大化目标
$$\mathbb{E}_{\boldsymbol{x}\sim \tilde{p}(\boldsymbol{x})} \big[\log q(\boldsymbol{x})\big]\tag{2}$$
然而$q_{\boldsymbol{\theta}}(\boldsymbol{x})$是积分形式的,能不能算下去很难说。
于是各路大神就“八仙过海,各显神通”了。其中,VAE和GAN在不同方向上避开了这个困难。VAE没有直接优化目标$(2)$,而是优化一个更强的上界,这使得它只能是一个近似模型,无法达到良好的生成效果。GAN则是通过一个交替训练的方法绕开了这个困难,确实保留了模型的精确性,所以它才能有如此好的生成效果。但不管怎么样,GAN也不能说处处让人满意了,所以探索别的解决方法是有意义的。
直面概率积分 #
flow模型选择了一条“硬路”:直接把积分算出来。
具体来说,flow模型选择$q(\boldsymbol{x}|\boldsymbol{z})$为狄拉克分布$\delta(\boldsymbol{x}-\boldsymbol{g}(\boldsymbol{z}))$,而且$\boldsymbol{g}(\boldsymbol{z})$必须是可逆的,也就是说
$$\boldsymbol{x}=\boldsymbol{g}(\boldsymbol{z}) \Leftrightarrow \boldsymbol{z} = \boldsymbol{f}(\boldsymbol{x})\tag{3}$$
要从理论上(数学上)实现可逆,那么要求$\boldsymbol{z}$和$\boldsymbol{x}$的维度一样。假设$\boldsymbol{f},\boldsymbol{g}$的形式都知道了,那么通过$(1)$算$q(\boldsymbol{x})$相当于是对$q(\boldsymbol{z})$做一个积分变换$\boldsymbol{z}=\boldsymbol{f}(\boldsymbol{x})$。即本来是
$$q(\boldsymbol{z}) = \frac{1}{(2\pi)^{D/2}}\exp\left(-\frac{1}{2} \Vert \boldsymbol{z}\Vert^2\right)\tag{4}$$
的标准高斯分布($D$是$\boldsymbol{z}$的维度),现在要做一个变换$\boldsymbol{z}=\boldsymbol{f}(\boldsymbol{x})$。注意概率密度函数的变量代换并不是简单地将$\boldsymbol{z}$替换为$\boldsymbol{f}(\boldsymbol{x})$就行了,还多出了一个“雅可比行列式”的绝对值,也就是
$$q(\boldsymbol{x}) = \frac{1}{(2\pi)^{D/2}}\exp\left(-\frac{1}{2}\big\Vert \boldsymbol{f}(\boldsymbol{x})\big\Vert^2\right)\left|\det\left[\frac{\partial \boldsymbol{f}}{\partial \boldsymbol{x}}\right]\right|\tag{5}$$
这样,对$\boldsymbol{f}$我们就有两个要求:
1、可逆,并且易于求逆函数(它的逆$\boldsymbol{g}$就是我们希望的生成模型);
2、对应的雅可比行列式容易计算。
这样一来
$$\log q(\boldsymbol{x}) = -\frac{D}{2}\log (2\pi) -\frac{1}{2}\big\Vert \boldsymbol{f}(\boldsymbol{x})\big\Vert^2 + \log \left|\det\left[\frac{\partial \boldsymbol{f}}{\partial \boldsymbol{x}}\right]\right|\tag{6}$$
这个优化目标是可以求解的。并且由于$\boldsymbol{f}$容易求逆,因此一旦训练完成,我们就可以随机采样一个$\boldsymbol{z}$,然后通过$\boldsymbol{f}$的逆来生成一个样本$\boldsymbol{f}^{-1}(\boldsymbol{z})=\boldsymbol{g}(\boldsymbol{z})$,这就得到了生成模型。
flow #
前面我们已经介绍了flow模型的特点和难点,下面我们来详细展示flow模型是如何针对难点来解决问题的。因为本文主要是介绍第一篇文章《NICE: Non-linear Independent Components Estimation》的工作,因此本文的模型也专称为NICE。
分块耦合层 #
相对而言,行列式的计算要比函数求逆要困难,所以我们从“要求2”出发思考。熟悉线性代数的朋友会知道,三角阵的行列式最容易计算:三角阵的行列式等于对角线元素之积。所以我们应该要想办法使得变换$\boldsymbol{f}$的雅可比矩阵为三角阵。NICE的做法很精巧,它将$D$维的$\boldsymbol{x}$分为两部分$\boldsymbol{x}_1, \boldsymbol{x}_2$,然后取下述变换:
$$\begin{aligned}&\boldsymbol{h}_{1} = \boldsymbol{x}_{1}\\
&\boldsymbol{h}_{2} = \boldsymbol{x}_{2} + \boldsymbol{m}(\boldsymbol{x}_{1})\end{aligned}\tag{7}$$
其中$\boldsymbol{x}_1, \boldsymbol{x}_2$是$\boldsymbol{x}$的某种划分,$\boldsymbol{m}$是$\boldsymbol{x}_1$的任意函数。也就是说,将$\boldsymbol{x}$分为两部分,然后按照上述公式进行变换,得到新的变量$\boldsymbol{h}$,这个我们称为“加性耦合层”(Additive Coupling)。不失一般性,可以将$\boldsymbol{x}$各个维度进行重排,使得$\boldsymbol{x}_1 = \boldsymbol{x}_{1:d}$为前$d$个元素,$\boldsymbol{x}_2=\boldsymbol{x}_{d+1:D}$为$d+1\sim D$个元素。
不难看出,这个变换的雅可比矩阵$\left[\frac{\partial \boldsymbol{h}}{\partial \boldsymbol{x}}\right]$是一个三角阵,而且对角线全部为1,用分块矩阵表示为
$$\left[\frac{\partial \boldsymbol{h}}{\partial \boldsymbol{x}}\right]=\begin{pmatrix}\mathbb{I}_{1:d} & \mathbb{O} \\
\left[\frac{\partial \boldsymbol{m}}{\partial \boldsymbol{x}_1}\right] & \mathbb{I}_{d+1:D}\end{pmatrix}\tag{8}$$
这样一来,这个变换的雅可比行列式为1,其对数为0,这样就解决了行列式的计算问题。
同时,$(7)$式的变换也是可逆的,其逆变换为
$$\begin{aligned}&\boldsymbol{x}_{1} = \boldsymbol{h}_{1}\\
&\boldsymbol{x}_{2} = \boldsymbol{h}_{2} - \boldsymbol{m}(\boldsymbol{h}_{1})\end{aligned}\tag{9}$$
细水长flow #
上面的变换让人十分惊喜:可逆,而且逆变换也很简单,并没有增加额外的计算量。尽管如此,我们可以留意到,变换$(7)$的第一部分是平凡的(恒等变换),因此单个变换不能达到非常强的非线性,所以我们需要多个简单变换的复合,以达到强非线性,增强拟合能力。
$$\boldsymbol{x} = \boldsymbol{h}^{(0)} \leftrightarrow \boldsymbol{h}^{(1)} \leftrightarrow \boldsymbol{h}^{(2)} \leftrightarrow \dots \leftrightarrow \boldsymbol{h}^{(n-1)} \leftrightarrow \boldsymbol{h}^{(n)} = \boldsymbol{z}\tag{10}$$
其中每个变换都是加性耦合层。这就好比流水一般,积少成多,细水长流,所以这样的一个流程成为一个“流(flow)”。也就是说,一个flow是多个加性耦合层的耦合。
由链式法则
$$\left[\frac{\partial \boldsymbol{z}}{\partial \boldsymbol{x}}\right]=\left[\frac{\partial \boldsymbol{h}^{(n)}}{\partial \boldsymbol{h}^{(0)}}\right]=\left[\frac{\partial \boldsymbol{h}^{(n)}}{\partial \boldsymbol{h}^{(n-1)}}\right]\left[\frac{\partial \boldsymbol{h}^{(n-1)}}{\partial \boldsymbol{h}^{(n-2)}}\right]\dots \left[\frac{\partial \boldsymbol{h}^{(1)}}{\partial \boldsymbol{h}^{(0)}}\right]\tag{11}$$
因为“矩阵的乘积的行列式等于矩阵的行列式的乘积”,而每一层都是加性耦合层,因此每一层的行列式为1,所以结果就是
$$\det \left[\frac{\partial \boldsymbol{z}}{\partial \boldsymbol{x}}\right]=\det\left[\frac{\partial \boldsymbol{h}^{(n)}}{\partial \boldsymbol{h}^{(n-1)}}\right]\det\left[\frac{\partial \boldsymbol{h}^{(n-1)}}{\partial \boldsymbol{h}^{(n-2)}}\right]\dots \det\left[\frac{\partial \boldsymbol{h}^{(1)}}{\partial \boldsymbol{h}^{(0)}}\right]=1$$
(考虑到下面的错位,行列式可能变为-1,但绝对值依然为1),所以我们依然不用考虑行列式。
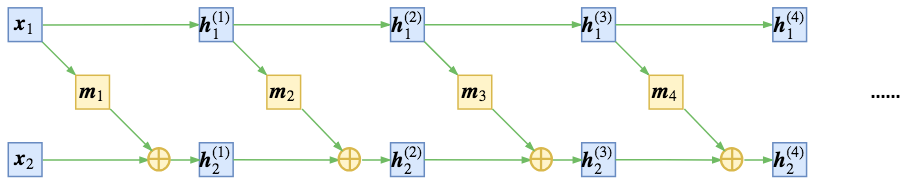
交错中前进 #
要注意,如果耦合的顺序一直保持不变,即
$$\begin{array}{ll}\begin{aligned}&\boldsymbol{h}^{(1)}_{1} = \boldsymbol{x}_{1}\\
&\boldsymbol{h}^{(1)}_{2} = \boldsymbol{x}_{2} + \boldsymbol{m}_1(\boldsymbol{x}_{1})\end{aligned} & \begin{aligned}&\boldsymbol{h}^{(2)}_{1} = \boldsymbol{h}^{(1)}_{1}\\
&\boldsymbol{h}^{(2)}_{2} = \boldsymbol{h}^{(1)}_{2} + \boldsymbol{m}_2\big(\boldsymbol{h}^{(1)}_{1}\big)\end{aligned} & \\
& \\
\begin{aligned}&\boldsymbol{h}^{(3)}_{1} = \boldsymbol{h}^{(2)}_{1}\\
&\boldsymbol{h}^{(3)}_{2} = \boldsymbol{h}^{(2)}_{2} + \boldsymbol{m}_3\big(\boldsymbol{h}^{(2)}_{1}\big)\end{aligned} & \begin{aligned}&\boldsymbol{h}^{(4)}_{1} = \boldsymbol{h}^{(3)}_{1}\\
&\boldsymbol{h}^{(4)}_{2} = \boldsymbol{h}^{(3)}_{2} + \boldsymbol{m}_4\big(\boldsymbol{h}^{(3)}_{1}\big)\end{aligned} & \quad\dots
\end{array}\tag{12}$$
那么最后还是$\boldsymbol{z}_1 = \boldsymbol{x}_1$,第一部分依然是平凡的,如下图
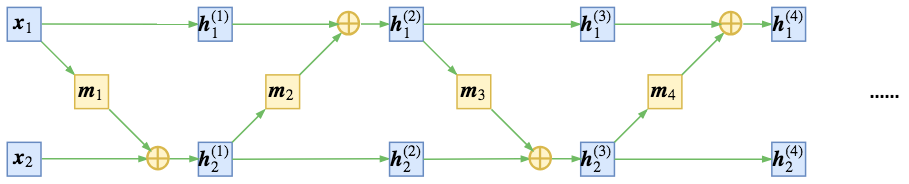
为了得到不平凡的变换,我们可以考虑在每次进行加性耦合前,打乱或反转输入的各个维度的顺序,或者简单地直接交换这两部分的位置,使得信息可以充分混合,比如
$$\begin{array}{ll}\begin{aligned}&\boldsymbol{h}^{(1)}_{1} = \boldsymbol{x}_{1}\\
&\boldsymbol{h}^{(1)}_{2} = \boldsymbol{x}_{2} + \boldsymbol{m}_1(\boldsymbol{x}_{1})\end{aligned} & \begin{aligned}&\boldsymbol{h}^{(2)}_{1} = \boldsymbol{h}^{(1)}_{1} + \boldsymbol{m}_2\big(\boldsymbol{h}^{(1)}_{2}\big)\\
&\boldsymbol{h}^{(2)}_{2} = \boldsymbol{h}^{(1)}_{2}\end{aligned} & \\
& \\
\begin{aligned}&\boldsymbol{h}^{(3)}_{1} = \boldsymbol{h}^{(2)}_{1}\\
&\boldsymbol{h}^{(3)}_{2} = \boldsymbol{h}^{(2)}_{2} + \boldsymbol{m}_3\big(\boldsymbol{h}^{(2)}_{1}\big)\end{aligned} & \begin{aligned}&\boldsymbol{h}^{(4)}_{1} = \boldsymbol{h}^{(3)}_{1} + \boldsymbol{m}_4\big(\boldsymbol{h}^{(3)}_{2}\big)\\
&\boldsymbol{h}^{(4)}_{2} = \boldsymbol{h}^{(3)}_{2} \end{aligned} & \quad\dots
\end{array}\tag{13}$$
如下图
尺度变换层 #
在文章的前半部分我们已经指出过,flow是基于可逆变换的,所以当模型训练完成之后,我们同时得到了一个生成模型和一个编码模型。但也正是因为可逆变换,随机变量$\boldsymbol{z}$和输入样本$\boldsymbol{x}$具有同一大小。当我们指定$\boldsymbol{z}$为高斯分布时,它是遍布整个$D$维空间的,$D$也就是输入$\boldsymbol{x}$的尺寸。但虽然$\boldsymbol{x}$具有$D$维,但它未必就真正能遍布整个$D$维空间,比如MNIST图像虽然有784个像素,但有些像素不管在训练集还是测试集,都一直保持为0,这说明它远远没有784维那么大。
也就是说,flow这种基于可逆变换的模型,天生就存在比较严重的维度浪费问题:输入数据明明都不是D维流形,但却要编码为一个D维流形,这可行吗?
为了解决这个情况,NICE引入了一个尺度变换层,它对最后编码出来的每个维度的特征都做了个尺度变换,也就是$\boldsymbol{z} = \boldsymbol{s}\otimes \boldsymbol{h}^{(n)}$这样的形式,其中$\boldsymbol{s} = (\boldsymbol{s}_1,\boldsymbol{s}_2,\dots,\boldsymbol{s}_D)$也是一个要优化的参数向量(各个元素非负)。这个$\boldsymbol{s}$向量能识别该维度的重要程度(越小越重要,越大说明这个维度越不重要,接近可以忽略),起到压缩流形的作用。注意这个尺度变换层的雅可比行列式就不再是1了,可以算得它的雅可比矩阵为对角阵
$$\left[\frac{\partial \boldsymbol{z}}{\partial \boldsymbol{h}^{(n)}}\right] = \text{diag}\, (\boldsymbol{s})\tag{14}$$
所以它的行列式为$\prod_i \boldsymbol{s}_i$。于是根据$(6)$式,我们有对数似然
$$\log q(\boldsymbol{x}) \sim -\frac{1}{2}\big\Vert \boldsymbol{s}\otimes \boldsymbol{f} (\boldsymbol{x})\big\Vert^2 + \sum_i \log \boldsymbol{s}_i\tag{15}$$
为什么这个尺度变换能识别特征的重要程度呢?其实这个尺度变换层可以换一种更加清晰的方式描述:我们开始设$\boldsymbol{z}$的先验分布为标准正态分布,也就是各个方差都为1。事实上,我们可以将先验分布的方差也作为训练参数,这样训练完成后方差有大有小,方差越小,说明该特征的“弥散”越小,如果方差为0,那么该特征就恒为均值0,该维度的分布坍缩为一个点,于是这意味着流形减少了一维。
不同于$(4)$式,我们写出带方差的正态分布:
$$q(\boldsymbol{z}) = \frac{1}{(2\pi)^{D/2}\prod\limits_{i=1}^D \boldsymbol{\sigma}_i}\exp\left(-\frac{1}{2}\sum_{i=1}^D \frac{\boldsymbol{z}_i^2}{\boldsymbol{\sigma}_i^2}\right)\tag{16}$$
将流模型$\boldsymbol{z}=\boldsymbol{f}(\boldsymbol{x})$代入上式,然后取对数,类似$(6)$式,我们得到
$$\log q(\boldsymbol{x}) \sim -\frac{1}{2}\sum_{i=1}^D \frac{\boldsymbol{f}_i^2(\boldsymbol{x})}{\boldsymbol{\sigma}_i^2} - \sum_{i=1}^D \log \boldsymbol{\sigma}_i\tag{17}$$
对比$(15)$式,其实就有$\boldsymbol{s}_i=1/\boldsymbol{\sigma}_i$。所以尺度变换层等价于将先验分布的方差(标准差)也作为训练参数,如果方差足够小,我们就可以认为该维度所表示的流形坍缩为一个点,从而总体流形的维度减1,暗含了降维的可能。
特征解耦 #
当我们将先验分布选为各分量独立的高斯分布时,除了采样上的方便,还能带来什么好处呢?
在flow模型中,$\boldsymbol{f}^{-1}$是生成模型,可以用来随机生成样本,那么$\boldsymbol{f}$就是编码器。但是不同于普通神经网络中的自编码器“强迫低维重建高维来提取有效信息”的做法,flow模型是完全可逆的,那么就不存在信息损失的问题,那么这个编码器还有什么价值呢?
这就涉及到了“什么是好的特征”的问题了。在现实生活中,我们经常抽象出一些维度来描述事物,比如“高矮”、“肥瘦”、“美丑”、“贫富”等,这些维度的特点是:“当我们说一个人高时,他不是必然会肥或会瘦,也不是必然会有钱或没钱”,也就是说这些特征之间没有多少必然联系,不然这些特征就有冗余了。所以,一个好的特征,理想情况下各个维度之间应该是相互独立的,这样实现了特征的解耦,使得每个维度都有自己独立的含义。
这样,我们就能理解“先验分布为各分量独立的高斯分布”的好处了,由于各分量的独立性,我们有理由说当我们用$\boldsymbol{f}$对原始特征进行编码时,输出的编码特征$\boldsymbol{z}=\boldsymbol{f}(\boldsymbol{x})$的各个维度是解耦的。NICE的全称Non-linear Independent Components Estimation,翻译为“非线性独立成分估计”,就是这个含义。反过来,由于$\boldsymbol{z}$的每个维度的独立性,理论上我们控制改变单个维度时,就可以看出生成图像是如何随着该维度的改变而改变,从而发现该维度的含义。
类似地,我们也可以对两幅图像的编码进行插值(加权平均),得到过渡自然的生成样本,这些在后面发展起来的glow模型中体现得很充分。不过,我们后面只做了MNIST实验,所以本文中就没有特别体现这一点。
实验 #
这里我们用Keras重现NICE一文中的MNIST的实验。
模型细节 #
先来把NICE模型的各个部分汇总一下。NICE模型是flow模型的一种,由多个加性耦合层组成,每个加性耦合层如$(7)$,它的逆是$(9)$。在耦合之前,需要反转输入的维度,使得信息充分混合。最后一层需要加个尺度变换层,最后的loss是$(15)$式的相反数。
加性耦合层需要将输入分为两部分,NICE采用交错分区,即下标为偶数的作为第一部分,下标为奇数的作为第二部分,而每个$\boldsymbol{m}(\boldsymbol{x})$则简单地用多层全连接(5个隐藏层,每个层1000节点,relu激活)。在NICE中一共耦合了4个加性耦合层。
对于输入,我们将原来是0~255的图像像素压缩为0~1之间(直接除以255),然后给输入加上噪声$[-0.01, 0]$的均匀分布噪声。噪声的加入能够有效地防止过拟合,提高生成的图片质量。它也可以看成是缓解维度浪费问题的一个措施,因为实际上MNIST的图像没有办法充满784维,但如果算上噪声,维度就增加了。
读者或许会好奇,为什么是噪声区间是$[-0.01, 0]$,而不是$[0, 0.01]$或$[-0.005, 0.005]$?事实上从loss看来各种噪声都差不多(包括将均匀分布换成高斯分布)。但是加入噪声后,理论上生成的图片也会带有噪声,这不是我们希望的,而加入负噪声,会让最终生成的图片的像素值稍微偏向负区间,这样我只要用clip操作就可以去掉一部分噪声,这是针对MNIST的一个(不是特别重要的)小技巧罢了。
参考代码 #
这里是我用Keras实现的参考代码:
https://github.com/bojone/flow/blob/master/nice.py
在我的实验中,20个epoch内可以跑到最优,11s一个epoch(GTX1070环境),最终的loss约为-2200。
相比于原论文的实现,这里做了一些改动。对于加性耦合层,我用了$(9)$式作为前向,$(7)$式作为其逆向。因为$\boldsymbol{m}(\boldsymbol{x})$用relu激活,我们知道relu是非负的,因此两种选择是有点差别的。因为正向是编码器,而逆向是生成器,选用$(7)$式作为逆向,那么生成模型更倾向于生成正数,这跟我们要生成的图像是吻合的,因为我们需要生成的是像素值为0~1的图像。
退火参数 #
虽然我们最终希望从标准正态分布中采样随机数来生成样本,但实际上对于训练好的模型,理想的采样方差并不一定是1,而是在1上下波动,一般比1稍小。最终采样的正态分布的标准差,我们称之为退火参数。比如上面的参考实现中,我们的退火参数选为0.75,目测在这时候生成模型的质量最优。
总结 #
NICE的模型还是比较庞大的,按照上述模型,模型的参数量约为$4 \times 5 \times 1000^2 = 2\times 10^7$,也就是两千万的参数只为训练一个MNIST生成模型,也是夸张~
NICE整体还是比较简单粗暴的,首先加性耦合本身比较简单,其次模型$\boldsymbol{m}$部分只是简单地用到了庞大的全连接层,还没有结合卷积等玩法,因此探索空间还有很大,Real NVP和glow就是它们的两个改进版本,它们的故事我们后面再谈。
转载到请包括本文地址:https://kexue.fm/archives/5776
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Aug. 11, 2018). 《细水长flow之NICE:流模型的基本概念与实现 》[Blog post]. Retrieved from https://kexue.fm/archives/5776
@online{kexuefm-5776,
title={细水长flow之NICE:流模型的基本概念与实现},
author={苏剑林},
year={2018},
month={Aug},
url={\url{https://kexue.fm/archives/5776}},
}













August 22nd, 2018
浏览你的网站都有一段时间。看你的文章,条理性、逻辑性、完整性都很强。
对于机器学习,你好像很有一套。自己鬼使神差选择化学,至今还在数据分析
的外面游荡。奇缘的是,之前一直在广州上班,现在来了新兴:你的老家。
所以,有机会的话分享、介绍一下数据方面的东西。个人觉得自己的数学思想还算可以。
看看是否有机会入门了解一下数据分析方面的实践。
感谢谬赞~
欢迎来到新兴,哈哈。你到新兴工作?还是路过?
有时间会尽量准备一些入门实践的。
August 28th, 2018
您好!最近在研究基于流的生成模型,非常感谢您详细的解读,但是有一个问题想要向您请教:对于图像x来说,像素值的取值是离散的,NICE模型将x的分布拟合为连续的高斯模型,那么是否可以求出x中每个像素值对应的概率呢?如果可以的话,应该怎么求呢?
想了一下,感觉很难,要写出概率密度的具体形式(包括雅可比行列式),还有数值积分...
嗯…那看来用这个方法求某个特定x的概率是不大行得通了呢,感谢回复!
你就是为了估计概率?可以考虑pixelrnn/pixelcnn之类的方法,直接输出概率。
是的,我是想要估计x的先验概率,确实pixelrnn之类可以估计,就是想试一下用这个方法行不行的通。昨天我又想了一下,还是有两个问题请教:
1. 假如x每一维的取值范围都是0,1,2...255,那这样的话,如果求q(x+u)du在u[-0.5,0.5)这个区间上的积分,是不是就是p(x)的概率呢?
2. 当u在[-0.5,0.5)这个范围的时候,映射到z空间的是否也是一个连续的区间呢?还是说,映射到z空间以后,映射过去的点是分散到各处的呢?
September 19th, 2018
原文“假设f,g的形式都知道了,那么通过(1)算q(x)相当于是对q(z)做一个积分变换z=f(x)。”
可能是我数学功底不扎实,所以我对公式4怎么来的不是很理解。
公式1是我们假设的一个分布,其实本文关键就是找出真实数据x到高维空间的映射f。
emmmm,到(4)是有什么公式?
$(1),(4)$都是假设,两个假设合并起来算出来的结果就是$(5)$,也就是说现在假设数据服从分布$(5)$。但是$(5)$的参数还没有确定,所以直接通过最大似然来确定$(5)$的参数。
October 17th, 2018
苏老师,您好,我想请教您一个问题。
我们经常使用的神经网络具有拟合很多固定映射的超能力,就好比 y=f(x)。训练成功以后我们就可以使用神经网络代替 f()。
但在一些推理问题中,有些映射是时变的或者动态的,比如一个随机分布。y = argmax P(y|x), 那深度学习里面有什么技术或者模型可以学习一种分布呢。
目前据我所知,GAN是可以学习分布的,但多用于分类问题,我想做的是一个回归问题,输出有多个预测值(包括时间延迟和一些散射角度),并不是图像或者自然语言的处理问题,想请问您有什么见解呢。
感谢您的阅读。希望能得到您的指点和灵感启发。
$y=f(x)$的$y$可以是一个向量,可以输出多个预测值。
难道你想说你要输出向量的分布?
我觉得需要一个比较具体的例子来表明你的需求。
大概是这样的一个system model。
$\mathbf{y} = \mathbf{\Phi}(\theta,\tau) \mathbf x+ \mathbf n$,其中 $\mathbf n$ 是高斯噪声。$\mathbf x$ 和 $\mathbf y$ 已知。 $\mathbf \phi(\theta,\tau)$ 待估计。
我考虑这个模型是否可以通过概率拟合以及生成模型来求解 $\mathbf \Phi(\theta,\tau)$。
你这是随机微分方程的参数估计问题?这个可以用gan来做,我做过...
苏老师,那是否可以把您做过的这个博客或paper分享一下链接呢,我想学习一下。。。
不好意思,还没有写出来过。
苏老师,再麻烦问一下,基于期望最大化的多参数估计 $\hat{\boldsymbol \theta}_i = (\phi_{i,t},\phi_{i,r}, d_i)$ 问题,可以利用深度学习来做吗,您有什么好的想法呢?
October 17th, 2018
“在我的实验中,20个epoch内可以跑到最优,11s一个epoch(GTX1070环境),最终的loss约为-2200。”
想问下 楼主用GTX1070 跑了多久呢~
20*11还需要我来算?
October 19th, 2018
@icaoys|comment-9977
具体情况具体分析~
October 19th, 2018
苏老师 您好
我想问您一个问题 您在VAE(变分自编码)中 算均值和方差直接2层神经网络
x = Input(shape=(original_dim,))
h = Dense(intermediate_dim, activation='relu')(x)
# 算p(Z|X)的均值和方差
z_mean = Dense(latent_dim)(h)
z_log_var = Dense(latent_dim)(h)
是不是应该算出所有的均值和方差 然后在放入神经网络中???
我这个不是很了解
所有的均值和方差是什么意思?
z_mean = Dense(latent_dim)(h)
z_log_var = Dense(latent_dim)(h)
这两句不是算均值和方差的吗?
November 20th, 2018
你好,请问代码中的Scale类的增加权重部分,为什么已经带了$\log$?那个$self.kernel$是$\log s_i$ ?
正是。
November 26th, 2018
博主你好,请教你个问题。“这个s向量能识别该维度的重要程度(越小越重要,越大说明这个维度越不重要,接近可以忽略),起到压缩流形的作用。”
这个不应该是越大越重要吗?越小的话说明方差越小,这个维度没什么区分性呀
s不是方差,s是方差的倒数。s越大,方差越小。
November 28th, 2018
博主,我想问个问题:能否人为固定z的某些维度的方差为比较小的值(比如通过固定scale层的参数),而其余部分正常训练,这样达到降维的效果?按照现有nice或者realnvp的拟合能力,这样的降维靠谱吗
思路没错,人为不行。事实上尺度变换层就能把该降维的方差学习好了,训练完模型之后,可以手动查看尺度变换层的方差,来决定保留哪些维度。问题是这样的方案(包括你的构思)训练成本依然没有改变,而flow之类的模型,主要是训练成本大。