让炼丹更科学一些（六）：自上而下的精妙构造

在《让炼丹更科学一些（五）：基于梯度精调学习率》中，我们进入了基于梯度来调度学习率的新篇章。但上文末也提到，在推导动态梯度下终点损失的最优学习率时，我们遇到了证明上的困难，具体来说，我们基于变分法“猜”出来的最优学习率序列，代入结论中进行放缩验证会十分困难，因此别说最优解了，我们甚至无法判断这个序列是否是可行解。

而在本文中，我们将通过一个精妙的构造得到更精准的结论，从而解决这个问题。就证明过程来看，这一次的结论可能已经达到了无法改进的精度。这个突破依然出自论文《Optimal Linear Decay Learning Rate Schedules and Further Refinements》。

问题回顾 #

先重温一下之前的结论。上文末，我们得到了《让炼丹更科学一些（四）：新恒等式，新学习率》结论的一般版本：
\begin{equation}\mathbb{E}[L(\boldsymbol{\theta}_T) - L(\boldsymbol{\theta}^*)] \leq \frac{R^2}{2\eta_{1:T}} + \frac{1}{2}\sum_{t=1}^T\frac{\eta_t^2 G_t^2}{\eta_{\min(t+1, T):T}}\label{leq:last-2}\end{equation}
我们想要求序列$\eta_1,\eta_2,\cdots,\eta_T\geq 0$，使得上式右端取最小值。通过连续近似和变分法，我们“猜测”答案是
\begin{equation}\eta_t = \frac{R G_t^{-2}}{\sqrt{Q_T}} (1 - Q_t/Q_T)\label{eq:opt-lr-last-x}\end{equation}
其中$Q_t=\sum_{k=1}^t G_k^{-2}$。然而，我们没法代入证明它，或者说要想证明它需要引入一些额外的假设。如果我们尝试代过，会发现主要问题是式$\eqref{leq:last-2}$右端的分母是$\eta_{t+1:T}$（$t < T$时），从而无法保证$\eta_t/\eta_{t+1:T}$有界，各种放缩会很困难。如果我们能将结论右端的分母进一步改进到$\eta_{t:T}$，那么证明将会“水到渠成”。

本文正是通过进一步提高结论$\eqref{leq:last-2}$的精度来完成最终证明的，但并非直接显式地改进它，而是通过小心谨慎的放缩，自上而下地构造出最优学习率序列，从而实现隐式地改进精度的效果。

小心放缩 #

具体来说，我们的出发点是《让炼丹更科学一些（四）：新恒等式，新学习率》中的恒等式
\begin{equation}\begin{aligned}
q_T =&\, \frac{1}{w_{1:T}}\sum_{t=1}^T w_t q_t + \sum_{k=1}^{T-1}\left(\frac{1}{w_{k+1:T}} - \frac{1}{w_{k:T}}\right)\sum_{t=k}^T w_t (q_t - q_k) \\
=&\, \frac{1}{w_{1:T}}\sum_{t=1}^T w_t q_t + \sum_{k=1}^{T-1}\left(\frac{1}{w_{k+1:T}} - \frac{1}{w_{k:T}}\right)\sum_{t=k+1}^T w_t (q_t - q_k)
\end{aligned}\label{eq:qt-g}\end{equation}
我们让$q_t = \mathbb{E}[L(\boldsymbol{\theta}_t) - L(\boldsymbol{\theta}^*)]$，$\mathbb{E}$是对全体$\boldsymbol{x}_1,\boldsymbol{x}_2,\cdots,\boldsymbol{x}_T$求期望，代入上式得
\begin{equation}\mathbb{E}[L(\boldsymbol{\theta}_T) - L(\boldsymbol{\theta}^*)] = \frac{1}{w_{1:T}}\sum_{t=1}^T w_t \mathbb{E}[L(\boldsymbol{\theta}_t) - L(\boldsymbol{\theta}^*)] + \sum_{k=1}^{T-1}\left(\frac{1}{w_{k+1:T}} - \frac{1}{w_{k:T}}\right)\sum_{t=k+1}^T w_t \mathbb{E}[L(\boldsymbol{\theta}_t) - L(\boldsymbol{\theta}_k)]\label{eq:qt-g2}\end{equation}
从现在开始，我们要紧记“非必要不放缩”的原则，以达到尽可能高的精度。现在我们利用凸性做第一次放缩：
\begin{gather}
\mathbb{E}[L(\boldsymbol{\theta}_t) - L(\boldsymbol{\theta}^*)] = \mathbb{E}[L(\boldsymbol{x}_t, \boldsymbol{\theta}_t) - L(\boldsymbol{x}_t, \boldsymbol{\theta}^*)] \leq \mathbb{E}[\boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)\cdot(\boldsymbol{\theta}_t - \boldsymbol{\theta}^*)] \\[4pt]
\mathbb{E}[L(\boldsymbol{\theta}_t) - L(\boldsymbol{\theta}_k)] = \mathbb{E}[L(\boldsymbol{x}_t, \boldsymbol{\theta}_t) - L(\boldsymbol{x}_t, \boldsymbol{\theta}_k)] \leq \mathbb{E}[\boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)\cdot(\boldsymbol{\theta}_t - \boldsymbol{\theta}_k)]
\end{gather}
注意这里要求每个$\boldsymbol{\theta}_t$至多依赖于$\boldsymbol{x}_1,\boldsymbol{x}_2,\cdots,\boldsymbol{x}_{t-1}$，这在随机优化中是能满足的，以及第二行的第一个等号还要求$t\geq k$，这也显然满足。代入到式$\eqref{eq:qt-g2}$得
\begin{equation}\mathbb{E}[L(\boldsymbol{\theta}_T) - L(\boldsymbol{\theta}^*)] \leq \underbrace{\frac{1}{w_{1:T}}\sum_{t=1}^T w_t \mathbb{E}[\boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)\cdot(\boldsymbol{\theta}_t - \boldsymbol{\theta}^*)]}_{(\text{A})} + \underbrace{\sum_{k=1}^{T-1}\left(\frac{1}{w_{k+1:T}} - \frac{1}{w_{k:T}}\right)\sum_{t=k+1}^T w_t \mathbb{E}[\boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)\cdot(\boldsymbol{\theta}_t - \boldsymbol{\theta}_k)]}_{(\text{B})}\label{leq:last-6-mid}\end{equation}
在文章《让炼丹更科学一些（四）：新恒等式，新学习率》中，接下来的步骤是分别对$\eqref{leq:last-6-mid}$的$(\text{A})$和$(\text{B})$进行放缩然后相加，分别放缩的处理方式放大了误差，给后续证明带来了麻烦。

恒等变换 #

因此，这一节我们将它们通过恒等变换合并成一个式子后再考虑放缩，以达到更高的精度。首先，还是假设学习率跟数据$\boldsymbol{x}_t$无关，那么可以将期望$\mathbb{E}$放到外边
\begin{equation}\mathbb{E}[L(\boldsymbol{\theta}_T) - L(\boldsymbol{\theta}^*)] \leq \mathbb{E}\Bigg[\underbrace{\frac{1}{w_{1:T}}\sum_{t=1}^T w_t \boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)\cdot(\boldsymbol{\theta}_t - \boldsymbol{\theta}^*)}_{(\text{A})} + \underbrace{\sum_{k=1}^{T-1}\left(\frac{1}{w_{k+1:T}} - \frac{1}{w_{k:T}}\right)\sum_{t=k+1}^T w_t \boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)\cdot(\boldsymbol{\theta}_t - \boldsymbol{\theta}_k)}_{(\text{B})}\Bigg]\end{equation}
比较复杂的是第二项，利用$\sum_{k=1}^{T-1}\sum_{t=k+1}^T = \sum_{t=1}^T \sum_{k=1}^{t-1}$交换求和次序得
\begin{equation}\begin{aligned}
(\text{B}) =&\, \sum_{t=1}^T \sum_{k=1}^{t-1}\left(\frac{1}{w_{k+1:T}} - \frac{1}{w_{k:T}}\right) w_t \boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)\cdot(\boldsymbol{\theta}_t - \boldsymbol{\theta}_k) \\
=&\, \sum_{t=1}^T w_t \boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)\cdot \sum_{k=1}^{t-1}\left(\frac{1}{w_{k+1:T}} - \frac{1}{w_{k:T}}\right) (\boldsymbol{\theta}_t - \boldsymbol{\theta}_k) \\
=&\, \sum_{t=1}^T w_t \boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)\cdot \left(\left(\frac{1}{w_{t:T}} - \frac{1}{w_{1:T}}\right)\boldsymbol{\theta}_t - \sum_{k=1}^{t-1}\left(\frac{1}{w_{k+1:T}} - \frac{1}{w_{k:T}}\right) \boldsymbol{\theta}_k\right) \\
\end{aligned}\end{equation}
加上$(\text{A})$后，刚好可以把$\frac{1}{w_{1:T}}w_t \boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)\cdot\boldsymbol{\theta}_t$这一项消去，剩下的整理得
\begin{equation}\mathbb{E}[L(\boldsymbol{\theta}_T) - L(\boldsymbol{\theta}^*)] \leq \mathbb{E}\Bigg[\frac{1}{w_{1:T}}\sum_{t=1}^T w_t \boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)\cdot\Bigg(\underbrace{\frac{w_{1:T}}{w_{t:T}}\boldsymbol{\theta}_t - w_{1:T}\sum_{k=1}^{t-1}\left(\frac{1}{w_{k+1:T}} - \frac{1}{w_{k:T}}\right) \boldsymbol{\theta}_k}_{\text{记为}\boldsymbol{\psi}_t} - \boldsymbol{\theta}^*\Bigg)\Bigg]\end{equation}
只要我们将上式所示部分记为$\boldsymbol{\psi}_t$，那么右端就具有标准的（加权）平均损失收敛的形式
\begin{equation}\mathbb{E}[L(\boldsymbol{\theta}_T) - L(\boldsymbol{\theta}^*)] \leq \mathbb{E}\Bigg[\frac{1}{w_{1:T}}\sum_{t=1}^T w_t \boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)\cdot(\boldsymbol{\psi}_t - \boldsymbol{\theta}^*)\Bigg] = \frac{1}{w_{1:T}}\sum_{t=1}^T w_t \mathbb{E}[\boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)\cdot(\boldsymbol{\psi}_t - \boldsymbol{\theta}^*)]\label{leq:last-6-mid2}\end{equation}

更新规则 #

根据$\boldsymbol{\psi}_t$的定义，可以直接验证成立：
\begin{equation}\boldsymbol{\psi}_{t+1} - \boldsymbol{\psi}_t = \frac{w_{1:T}}{w_{t+1:T}}(\boldsymbol{\theta}_{t+1} - \boldsymbol{\theta}_t)\end{equation}
因此，如果让$\boldsymbol{\psi}_t$按照$\boldsymbol{\psi}_{t+1} = \boldsymbol{\psi}_t - w_t \boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)$更新，那么将会有$\boldsymbol{\theta}_{t+1} = \boldsymbol{\theta}_t - \frac{w_t w_{t+1:T}}{w_{1:T}} \boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)$：
\begin{equation}\boldsymbol{\psi}_{t+1} = \boldsymbol{\psi}_t - w_t \boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)\qquad\Rightarrow\qquad\boldsymbol{\theta}_{t+1} = \boldsymbol{\theta}_t - \frac{w_t w_{t+1:T}}{w_{1:T}} \boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)\end{equation}
而按照这个规则更新的$\boldsymbol{\psi}_t$，我们在《让炼丹更科学一些（二）：将结论推广到无界域》、《让炼丹更科学一些（五）：基于梯度精调学习率》已经证明了，成立不等式
\begin{equation}\frac{1}{w_{1:T}}\sum_{t=1}^T w_t \mathbb{E}[\boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)\cdot(\boldsymbol{\psi}_t - \boldsymbol{\theta}^*)] \leq \frac{1}{2 w_{1:T}}\left(R^2 + \sum_{t=1}^T w_t^2 \mathbb{E}[\Vert\boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)\Vert^2]\right)\label{leq:avg-3}\end{equation}
其中$R = \Vert\boldsymbol{\psi}_1 - \boldsymbol{\theta}^*\Vert$，我们给$\boldsymbol{\psi}_t$和$\boldsymbol{\theta}_t$选择相同的起点，那么也有$R = \Vert\boldsymbol{\theta}_1 - \boldsymbol{\theta}^*\Vert$。

可能有读者觉得不对劲：上式中的$\boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)$是在$\boldsymbol{\theta}_t$处的梯度而不是$\boldsymbol{\psi}_t$处的梯度，是否不能代入之前的结论？对此，我们在《让炼丹更科学一些（五）：基于梯度精调学习率》特意说明过，设为当前点的梯度$\boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\psi}_t)$的作用是通过凸性建立起$\boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\psi}_t)\cdot(\boldsymbol{\psi}_t - \boldsymbol{\theta}^*)$与损失函数的关系，但这里并不需要这个关系，所以换成$\boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)$也是可以的。

最强结论 #

现在将结论$\eqref{leq:avg-3}$代入到式$\eqref{leq:last-6-mid2}$，进行第二次放缩，得到
\begin{equation}\mathbb{E}[L(\boldsymbol{\theta}_T) - L(\boldsymbol{\theta}^*)] \leq \frac{1}{2 w_{1:T}}\left(R^2 + \sum_{t=1}^T w_t^2 G_t^2\right)\label{leq:last-6}\end{equation}
这里记了$G_t^2 = \mathbb{E}[\Vert\boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)\Vert^2]$。也就是说，如果我们用学习率$\eta_t = \frac{w_t w_{t+1:T}}{w_{1:T}}$取执行SGD，那么它的终点损失满足上述不等式。由于更谨慎地进行了放缩，这个上界理论上比结论$\eqref{leq:last-2}$更准，但它相对隐式一些，因为它要求我们先从$\eta_t$中解出$w_t$，然后才能代入右端验证，然而显式求解$w_t$并不是朴素的事情。

不过我们可以反过来，推导出最优的$w_t$，然后由$\eta_t = \frac{w_t w_{t+1:T}}{w_{1:T}}$得到最优的$\eta_t$。上式右端的最小值，我们在上篇文章《让炼丹更科学一些（五）：基于梯度精调学习率》已经求出，答案是：
\begin{equation}w_t = \frac{R G_t^{-2}}{\sqrt{Q_T}},\qquad Q_T=\sum_{k=1}^T G_k^{-2}\end{equation}
那么最优的$\eta_t$便是
\begin{equation}\eta_t = \frac{w_t w_{t+1:T}}{w_{1:T}} = \frac{R G_t^{-2}}{\sqrt{Q_T}} (1 - Q_t/Q_T)\label{eq:opt-lr-last-x2}\end{equation}
这正好是式$\eqref{eq:opt-lr-last-x}$！至此，我们完成了式$\eqref{eq:opt-lr-last-x}$的最优性的证明。

而对于这个结果本身，我们在上篇文章已经做过初步解读：第一项$G_t^{-2}$反比于梯度模长平方，它可以解释早期Warmup的必要性，因为早期梯度通常较大；$1 - Q_t/Q_T$是单调衰减到零的，它解释了学习率衰减的必要性。特别地，如果假设梯度模长是常数，那么我们将得到线性衰减学习率，这是实践中常用的学习率策略。

事后调整 #

式$\eqref{eq:opt-lr-last-x2}$还能怎么指导实践呢？首先它本身是不符合因果律的，没法直接用，原论文《Optimal Linear Decay Learning Rate Schedules and Further Refinements》提供了一种事后检验/调整的做法。

思路其实很简单，就是随便选一个学习率策略先训一次，然后就可以根据梯度信息来计算最优学习率$\eqref{eq:opt-lr-last-x2}$，看它的曲线跟我们所选的学习率策略是否符合，如果偏离严重，那么需要调整学习率策略重新训练，这在论文中被称为“Refinement”。这个做法适合于正式训练之前，有很多前置准备实验的场景。

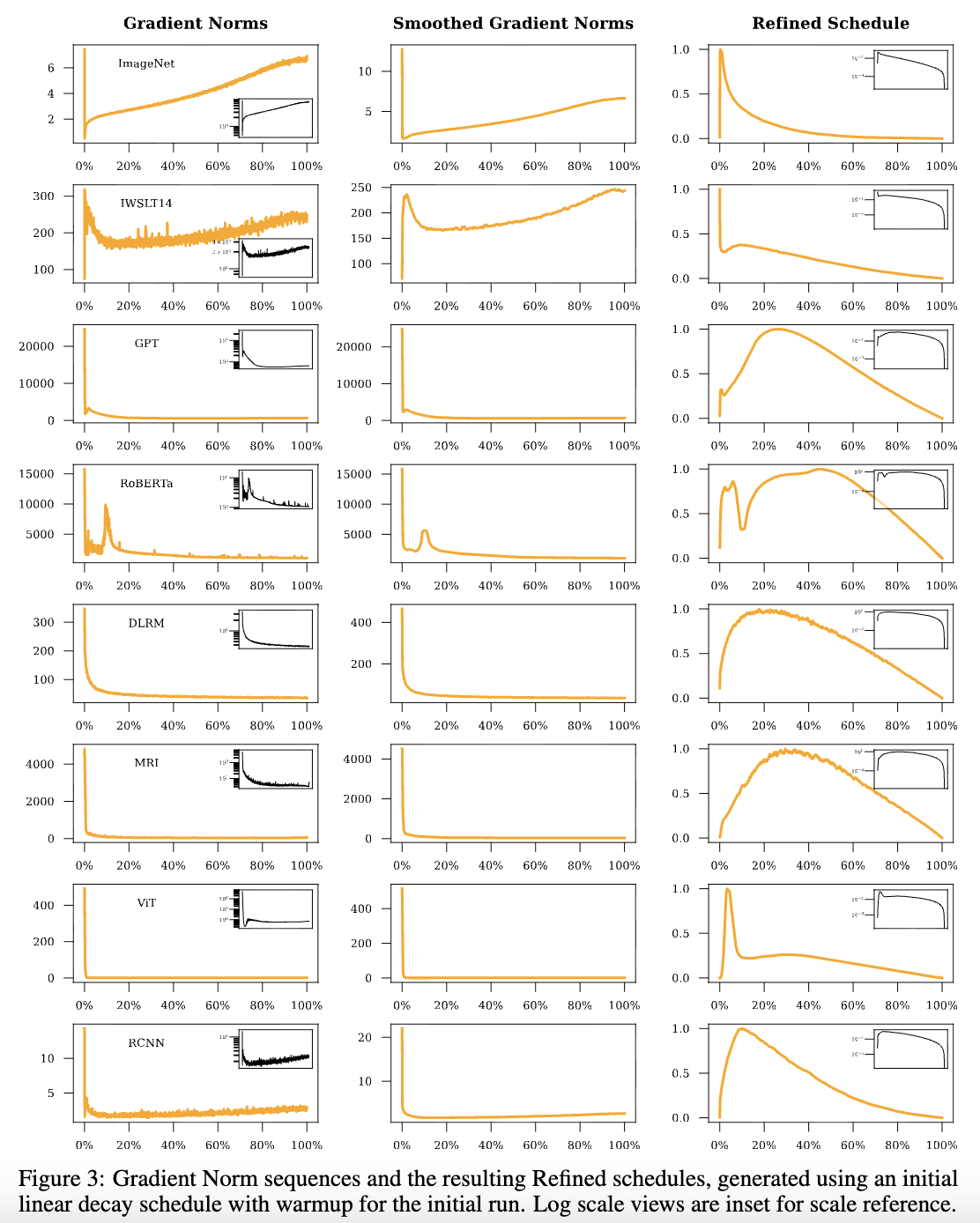
论文提供了一些Refined学习率的例子，大多数都呈现出“Warmup-Decay”的形式，特别地，大部份实验中后期的梯度模长都近乎常数，所以中后期的最优Decay形状都接近线性衰减：

最后，上述结果是针对SGD的，有$w_t\propto \mathbb{E}[\Vert\boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)\Vert^{-2}]$，实践中我们只能用$\Vert\boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)\Vert^2$近似，这里的$\Vert\cdot\Vert$是L2模长；而对于Adam等自适应学习率优化器，论文建议用$w_t\propto \mathbb{E}[\Vert\boldsymbol{g}(\boldsymbol{x}_t, \boldsymbol{\theta}_t)\Vert_1^{-1}]$，即反比于L1模长。关于自适应学习率优化器，我们后面的文章再谈。

显式版本 #

如果我们指定自己的学习率策略$\eta_t$，想要看它究竟有多优，目前看来还是比较麻烦的，因为式$\eqref{leq:last-6}$是一个半隐式的结论，要想代入右端检验，就必须要解方程$\eta_t = \frac{w_t w_{t+1:T}}{w_{1:T}}$，这方程说不上有多难解，主要是解并不简洁，不好用精确解来证明。

这里我们通过进一步的放缩，将它转化为关于$\eta_t$的显式结论。放缩稍微有点技巧，笔者也想了很久，但写出来后是挺好理解的：
\begin{equation}\eta_t = \frac{w_t w_{t+1:T}}{w_{1:T}} \leq \frac{w_t (w_{t:T} + w_{t+1:T})}{2 w_{1:T}} = \frac{w_{t:T}^2 - w_{t+1:T}^2}{2 w_{1:T}}\end{equation}
这里的$w_{t:T}^2$按照$(w_{t:T})^2$来理解。两端从$t\sim T$求和，得到\begin{equation}\eta_{t:T} \leq \frac{w_{t:T}^2}{2 w_{1:T}}\end{equation}
代入$t=1$可推得$\frac{1}{w_{1:T}} \leq \frac{1}{2\eta_{1:T}}$，然后将$t$换成$t+1$可推得$\frac{w_{1:T}}{w_{t+1:T}^2} \leq \frac{1}{2\eta_{t+1:T}}$，然后再结合$\eta_t$的定义可得$\frac{w_t^2}{w_{1:T}} = \eta_t^2 \frac{w_{1:T}}{w_{t+1:T}^2} \leq \frac{\eta_t^2}{2\eta_{t+1:T}}$。最后，将式$\eqref{leq:last-6}$右端稍加变形，并将这些不等式代入得
\begin{equation}\mathbb{E}[L(\boldsymbol{\theta}_T) - L(\boldsymbol{\theta}^*)] \leq \frac{R^2}{2 w_{1:T}} + \sum_{t=1}^T \frac{w_t^2}{2 w_{1:T}} G_t^2 \leq \frac{R^2}{4 \eta_{1:T}} + \sum_{t=1}^{T-2} \frac{\eta_t^2}{4\eta_{t+1:T}} G_t^2 + \frac{w_{T-1}^2}{2 w_{1:T}} G_{T-1}^2 + \frac{w_T^2}{2 w_{1:T}} G_T^2 \end{equation}
这里没有放缩最后两项，是因为按照$\eta_t = \frac{w_t w_{t+1:T}}{w_{1:T}}$的定义必然有$\eta_T=0$，那么$\frac{\eta_t^2}{2\eta_{t+1:T}}$在$t=T-1$和$t=T$时都是无穷大。这也告诉我们，$\eta_1,\eta_2,\cdots,\eta_T$实际上只有$T-1$个自由参数，但是对应的“未知数”$w_1,w_2,\cdots,w_T$却有$T$个，方程个数少于未知数个数，这就给我们提供了一个可以灵活调整的自由度。

还是根据定义，我们有$\eta_{T-1} = \frac{w_{T-1} w_T}{w_{1:T}}$，于是由基本不等式知
\begin{equation}\frac{w_{T-1}^2}{2 w_{1:T}} G_{T-1}^2 + \frac{w_T^2}{2 w_{1:T}}G_T^2 \geq \frac{w_{T-1} w_T}{w_{1:T}} G_{T-1}G_T = \eta_{T-1}G_{T-1}G_T \end{equation}
由于“灵活调整的自由度”的存在，我们可以适当的$w_{T-1},w_T$（即取$w_{T-1} G_{T-1} = w_T G_T$），使得上述不等式取到等号，于是
\begin{equation}\mathbb{E}[L(\boldsymbol{\theta}_T) - L(\boldsymbol{\theta}^*)] \leq \frac{R^2}{4 \eta_{1:T}} + \sum_{t=1}^{T-2} \frac{\eta_t^2}{4\eta_{t+1:T}} G_t^2 + \eta_{T-1} G_{T-1} G_T\end{equation}
这个结论笔者没发现在哪篇文献出现过，所以暂时认为它是新的，其精度要比$\eqref{leq:last-2}$高。当然，结论$\eqref{leq:last-2}$实际上不适用于终点为0的学习率序列，所以实际上也不大好直接比较，但从前两个主项的常系数来看，$\eqref{leq:last-2}$的是$1/2$，上式则是$1/4$，平均来说精度应该高上一倍。

文章小结 #

上文末我们提到终点损失的最优学习率策略的证明困难问题，而在这篇文章中，我们通过自上而下的、小心谨慎的放缩和构造，完成了这个证明，并得到了更高精度的结果，同时讨论了这个结果对学习率的“Warmup-Decay”机制的启发。

转载到请包括本文地址：https://kexue.fm/archives/11540

更详细的转载事宜请参考：《科学空间FAQ》