Mitchell近似:乘法变为加法,误差不超过1/9
By 苏剑林 | 2020-12-14 | 57406位读者 |今天给大家介绍一篇1962年的论文《Computer Multiplication and Division Using Binary Logarithms》,作者是John N. Mitchell,他在里边提出了一个相当有意思的算法:在二进制下,可以完全通过加法来近似完成两个数的相乘,最大误差不超过1/9。整个算法相当巧妙,更有意思的是它还有着非常简洁的编程实现,让人拍案叫绝。然而,笔者发现网上居然找不到介绍这个算法的网页,所以在此介绍一番。
你以为这只是过时的玩意?那你就错了,前不久才有人利用它发了一篇NeurIPS 2020呢!所以,确定不来了解一下吗?
快速对数与指数 #
说到乘法变加法,大家应该很自然能联想到对数和指数,即
\begin{equation}pq = a^s, \quad s = \log_a p + \log_a q\end{equation}
本文是基于二进制的,所以$a=2$。问题在于上式虽然确实将乘法转为加法了,但是对数$\log_2 p, \log_2 q$和转换后的指数$2^s$算起来都不是一件容易的事情。所以要利用这个等式做乘法,关键在于要实现快速对数和指数运算。
对于十进制的非负数$p$,我们假设它的二进制表示为
\begin{equation}z_n z_{n-1} \cdots z_1 z_0 . z_{-1} z_{-2} \cdots z_{-(m-1)} z_{-m}\end{equation}
其中$z_n = 1$且各个$z_i\in\{0,1\}$,那么我们就有
\begin{equation}p = 2^n + \sum_{i=-m}^{n-1} z_i 2^i = 2^n\left(1 + \sum_{i=-m}^{n-1} z_i 2^{i-n}\right)\end{equation}
记$x = \sum\limits_{i=-m}^{n-1} z_i 2^{i-n}$,我们得到
\begin{equation}\log_2 p = n + \log_2\left(1 + x\right)\end{equation}
在这里,Mitchell做了一个相当果断而美妙的近似,那就是$\log_2\left(1 + x\right)\approx x$(后面我们会再进行误差分析),于是得到
\begin{equation}\log_2 p \approx n + x\end{equation}
这个结果妙在何处呢?首先$n$是一个整数,等于$p$的二进制的整数部分的位数减去1,它转换为二进制自然自然也是整数;那$x$呢?根据$x$的定义我们不难看出,实际上$x$的二进制表示就是
\begin{equation}0 . z_{n-1} \cdots z_1 z_0 z_{-1} z_{-2} \cdots z_{-(m-1)} z_{-m}\end{equation}
也就是说$x$其实就是上述近似的小数部分,它的二进制表示只不过是$p$的二进制表示的简单变形(小数点平移)。
综上所述,我们得到对数的Mitchell近似算法:
1、输入十进制的$p$;
2、将$p$转换为二进制数$z_n z_{n-1} \cdots z_1 z_0 . z_{-1} z_{-2} \cdots z_{-(m-1)} z_{-m}$,这里$z_n=1$;
3、将$n$转换为二进制数$y_k y_{k-1} \cdots y_1 y_0$;
4、那么$\log_2 p$的二进制近似为$y_k y_{k-1} \cdots y_1 y_0 . z_{n-1} \cdots z_1 z_0 z_{-1} z_{-2} \cdots z_{-(m-1)} z_{-m}$。
将上述过程逆过来,就得到了指数的Mitchell近似算法:
1、输入二进制的$z_n z_{n-1} \cdots z_1 z_0 . z_{-1} z_{-2} \cdots z_{-(m-1)} z_{-m}$;
2、将$z_n z_{n-1} \cdots z_1 z_0$转换为十进制数$n$;
3、那么它的指数的二进制近似为$1 z_{-1} z_{-2} \cdots z_{-(n-1)} z_{-n} . z_{-(n+1)} z_{-(n+2)}\cdots z_{-(m-1)} z_{-m}$;
4、将上述结果转换为十进制。
所以,在二进制下对数和指数的近似计算就只是数数和拼接操作而已!惊艳不?神奇不?
一个乘法的例子 #
有了快速的(近似的)对数和指数算法,我们就可以乘法了,现在我们就用这个思路来算一个具体例子,由此加深我们对上述过程理解。
我们要算的是$12.3\times 4.56$,计算流程如下表(近似指数是对求和的结果算的):
$$\begin{array}{c|cc}
\hline
p,q|_\text{十进制} & 12.3 & 4.56 \\
\hline
p,q|_\text{二进制} & 1100.0100110 & 100.1000111 \\
\hline
n|_\text{十进制} & 3 & 2 \\
\hline
n|_\text{二进制} & 11 & 10 \\
\hline
x|_\text{二进制} & 0.1000100110 & 0.001000111 \\
\hline
n+x|_\text{二进制} & 11.1000100110 & 10.001000111 \\
\hline
\text{求和}|_\text{二进制} & \rlap{\,\,\,101.10101101} \\
\hline
n|_\text{二进制} & \rlap{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,101} \\
\hline
n|_\text{十进制} & \rlap{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,5} \\
\hline
x|_\text{二进制} & \rlap{\,\,\,\,\,\,0.10101101} \\
\hline
\text{近似指数}|_\text{二进制} & \rlap{\,\,\,\,\,\,110101.101} \\
\hline
\text{近似指数}|_\text{十进制} & \rlap{\,\,\,\,\,\,\,\,\,\,\,53.625} \\
\hline
\text{精确乘积}|_\text{十进制} & \rlap{\,\,\,\,\,\,\,\,\,\,\,56.088} \\
\hline
\text{相对误差}|_\text{十进制} & \rlap{\,\,\,\,\,\,\,\,\,\,\,\,4.39\%} \\
\hline
\end{array}$$
其中$p,q$二进制表示为无限循环小数,这里只截断了有限位,如果保留精确的二进制表示,那么最终结果是53.68,跟上表的53.625相差不大。可以看到,整个过程的主要计算量有两部分:求和、十进制与二进制之间的转换。然而,尽管十进制与二进制之间的转换对于我们人来说是计算量比较大的操作,但对于计算机来说,它本身就是二进制存储的,我们可以认为两者之间的转换计算量可以忽略不计;又或者说,只要我们还是以十进制为输出,那么不管什么算法这部分计算量都是必然存在的,因此我们不把它算进去算法的复杂度中。所以,整个算法的计算量就只有求和这一步,实现了将乘法(近似地)转化为加法运算。
神奇的C++实现 #
更妙的是,上述过程有一个非常简单的C++实现,参考如下:
#include<stdio.h>
int main() {
float a = 12.3f;
float b = 4.56f;
int c = *(int*)&a + *(int*)&b - 0x3f800000;
printf("近似结果:%f\n", *(float*)&c);
printf("精确结果:%f\n", a * b);
return 0;
}
没有C++编译环境的朋友也可以找个网页版的在线C++运行程序试跑一下,测试一下它的结果。就算是不懂C++的朋友(比如笔者)大概也可以感觉到,这段代码大概就是转化为两个数相加并且减去一个常数,这怎么就能实现乘法了?还有的读者可能问Python里边能这样写吗?
首先,后一个问题的答案是不能,因为Python的数据类型已经经过了高度封装了,而上述C++代码的可行性在于浮点数的IEEE754表示法:一个十进制浮点数首先会被转化为二进制,然后标准化为科学计数法,最后用一个特定的结构将科学计数法的结果存下来。具体来说,IEEE754用32个0/1表示一个浮点数,其中1位表示正负号(0为正),8位表示科学计数法的指数,23位表示科学计数法的小数,以9.75为例,它的二进制为1001.11,写成科学计数法就是$1.00111\times 10^{11}$,这里的10、11都是二进制,$10^{11}$对应十进制的$2^3$,注意指数部分我们还需要加上偏移量127,即3次方实际上存的是130(二进制表示为10000010),因为前面126个数要用来表示负整数幂,而主要部分1.00111,由于第一位必然是1,因此只需要把0.00111存下来,所以9.75背后的表示方式为:
\begin{array}{c|c|c}
\hline
\text{符号} & \text{指数} & \text{小数} \\
\hline
0 & 10000010 & 0011100\, 00000000\, 00000000 \\
\hline
\end{array}
知道IEEE754表示法之后,就可以理解上述代码了,*(int*)&a和*(int*)&b其实就是把$a,b$的IEEE754表示拿出来,当作普通的整数来运算,两者相加,其实正好对应着Mitchell近似对数后的相加结果,但是指数部分会多出一个偏移量,所以要减去整个偏移量,由于偏移量是127,并且后面还有23位,所以减去偏移量相当于减去常数$127\times 2^{23}$,表示为十六进制就是3f800000(因为二进制表示太长了,所以计算机一般用十六进制来代替二进制进行IO),最后将加减后的结果恢复为浮点数。
(注:其实笔者也不懂C++,上述理解是东拼西凑勉强得到的,如果不当之处,请大家指出。)
最大误差的分析 #
标题写到,这个算法的误差不超1/9,现在我们就来证明这一点。证明需要全部转换到十进制来理解,Mitchell近似实际上是用了如下近似式:
\begin{equation}\log_2 2^n(1+x)\approx n + x,\quad 2^{n+x}\approx 2^n(1+x)\end{equation}
其中$n$是整数,而$x\in[0, 1)$,所以分析误差也是从这两个近似入手。
假设两个数为$p=2^{n_1} (1 + x_1), q = 2^{n_2} (1 + x_2)$,那么根据近似就有$\log_2 p + \log_2 q \approx n_1 + n_2 + x_1 + x_2$,可见要分两种情况讨论:第一种情况$x_1 + x_2 < 1$,那么近似指数的结果就是$2^{n_1 + n_2}(1 + x_1 + x_2)$,因此近似程度就是
\begin{equation}\begin{aligned}
\frac{2^{n_1 + n_2}(1 + x_1 + x_2)}{2^{n_1} (1 + x_1)\times 2^{n_2} (1 + x_2)} = \frac{1 + x_1 + x_2}{1 + x_1 + x_2 + x_1 x_2}
\end{aligned}\end{equation}
第二种情况$x_1 + x_2 \geq 1$,这时候近似指数的结果就是$2^{n_1 + n_2 + 1}(x_1 + x_2)$,因此近似程度就是
\begin{equation}\begin{aligned}
\frac{2^{n_1 + n_2 + 1}(x_1 + x_2)}{2^{n_1} (1 + x_1)\times 2^{n_2} (1 + x_2)} = \frac{2 (x_1 + x_2)}{1 + x_1 + x_2 + x_1 x_2}
\end{aligned}\end{equation}
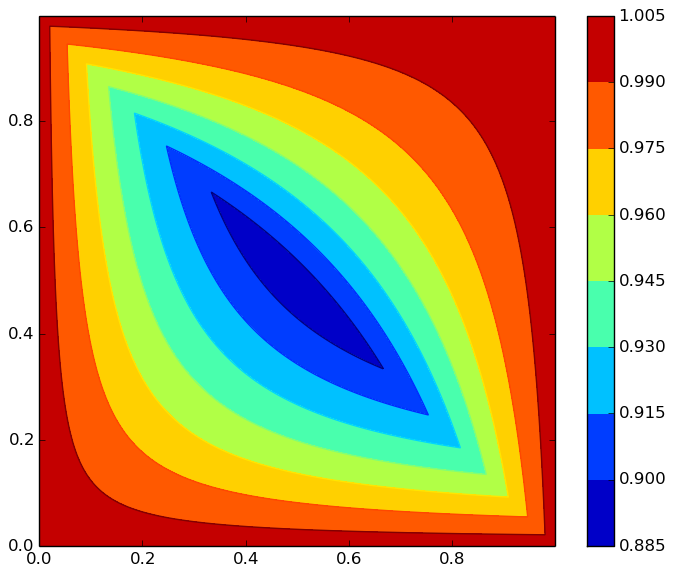
可以按部就班地证明,上面两种情况的最小值,都是在$x_1 = x_2 = 0.5$时取到,其结果为$8/9$,所以最大的相对误差为$1/9$(如果是除法变成减法,那么它的最大误差是$12.5\%$)。因为按部就班的证明有点繁琐,我们这里就不重复了,而是直接用软件画出它的等高线图,看出误差最大的地方应该是中心处:
作图代码:
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0, 1, 0.001)
y = np.arange(0, 1, 0.001)
X, Y = np.meshgrid(x, y)
Z1 = (1 + X + Y) / (1 + X + Y + X * Y)
Z2 = 2 * (X + Y) / (1 + X + Y + X * Y)
Z = (X + Y < 1) * Z1 + (X + Y >= 1) * Z2
plt.figure(figsize=(7, 6))
contourf = plt.contourf(X, Y, Z)
plt.contour(X, Y, Z)
plt.colorbar(contourf)
plt.show()其实这个误差本质上取决于$\log_2 (1 + x)\approx x$的近似程度,我们知道$x$是自然对数$\ln (1 + x)$的一阶泰勒展开式,而$e=2.71828\dots$更加接近于3,所以如果计算机使用3进制的话,本算法会有更高的平均精度。事实上,确实有一些理论分析表明,对于计算机来说其实最理想是$e$进制,而3比2更接近于$e$,所以三进制计算机在不少方面会比二进制更优,我国和前苏联都曾研究过三进制计算机,不过由于二进制实现起来更加容易,所以当前还是二进制计算机的天下了。
搬到深度学习中 #
Mitchell近似的介绍就到这里了。读者可能会困惑,这不该是计算机基础和数据机构那一块的东西吗?你研究它干嘛?还能在深度学习中有什么应用吗?
笔者学习它的原因有两个:一是它确实很漂亮,值得学习;二是它还真的可以用到深度学习中。事实上,笔者是NeurIPS 2020的一篇论文《Deep Neural Network Training without Multiplications》中发现它的,该论文在“ImageNet+ResNet50”验证了直接将神经网络中的乘法换成Mitchell近似的加法形式,准确率只有轻微的下降,甚至可能不下降。
当然,作者目前的实现只是验证了这种替换在效果上是可接受的,在速度上其实是变慢了的。这是因为虽然从理论上来讲乘法换成近似加法速度一定会有提升,但要实现这个提升需要从硬件底层进行优化才行,因为当前标准的乘法肯定也是经过了硬件级别的优化,所以作者是提供了未来深度学习硬件优化的一个方向吧。此外,Mitchell近似在深度学习中的应用分析,也不是第一次被讨论了,直接Google就可以搜到两篇,分别是《Efficient Mitchell’s Approximate Log Multipliers for Convolutional Neural Networks》和《Low-power implementation of Mitchell's approximate logarithmic multiplication for convolutional neural networks》。
可能读者联想到了华为之前提出的加法神经网络AdderNet,其目的确实有类似之处,但方法上其实差别很大。AdderNet是将神经网络的内积换成了$l_1$距离,从而去掉了乘法;这篇论文则是修改了乘法的实现,降低了乘法的计算量,已有的神经网络运算可能都可以保留下来。
也把新瓶装旧酒 #
本文介绍了1962年发表的Mitchell近似算法,它是一种近似的对数和指数计算,基于此我们可以将乘法转化为加法,并保持一定的精度。看上去已经过时,但将这个算法“新瓶装旧酒”一下,就成为了NeurIPS 2020中一篇论文了。
所以,你还发现了哪些可以装到新瓶的“旧酒”呢?
转载到请包括本文地址:https://kexue.fm/archives/7991
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Dec. 14, 2020). 《Mitchell近似:乘法变为加法,误差不超过1/9 》[Blog post]. Retrieved from https://kexue.fm/archives/7991
@online{kexuefm-7991,
title={Mitchell近似:乘法变为加法,误差不超过1/9},
author={苏剑林},
year={2020},
month={Dec},
url={\url{https://kexue.fm/archives/7991}},
}










December 14th, 2020
或许乘法计算本身可以视为是卷积的近似,而用1个电容就可以实现卷积的近似。
所以,从硬件上可以用一排电容近似实现向量的内积和求和。
电容体积太大了吧,可能量子计算更合适,
反正我看不懂。
确实有光计算实现的机器学习,就是模拟电路的。
December 21st, 2020
感觉这个算法应该和快速开平方的那个有些联系
直接的联系倒没有,只不过有些异曲同工的地方。
April 7th, 2021
目前乘法主要应用在了矩阵乘这一块,把这个计算应用到矩阵乘能快多少?有和mkl或者openblas这样的库比较过吗
目前的快都是理论上的,似乎要从硬件上优化才能真正超过标准乘法。
December 22nd, 2024
想请教下苏神,这个分情况的误差分析怎么得到的?我只能通过对$2^{n_1 + n_2}$进行泰勒展开,计算得到当$n_1 + n_2 = 1$时,如果展开项数到4-5阶时,这个相对误差可以小于1/9
对$2^{x_1 + x_2}$进行泰勒展开
不是很明白你的疑问是什么?误差分析的过程不是在文中给出了吗?