【理科生读小说】来谈谈“四两拨千斤”
By 苏剑林 | 2018-01-28 | 46464位读者 |多彩金庸 #
在金庸笔下(其实很多武侠小说都如此),武功可以分三种:第一种是实打实的猛,如洪七公的降龙十八掌、金轮法王的龙象般若功等,它们的特点是主要特点是刚猛,比如
乔峰的降龙二十八掌是丐帮前任帮主汪剑通所传,但乔峰生俱异禀,于武功上得天独厚,他这降龙二十八掌摧枯拉朽,无坚不破,较之汪帮主尤有胜过。乔峰见对方双掌齐推,自己如以单掌相抵,倘若拼成平手,自己似乎稍占上风,不免有失恭敬,于是也双掌齐出。他左右双掌中所使掌力,也仍都是外三内七,将大部分掌力留劲不发。
——出自《天龙八部》世纪新修版
第二种是以虚招为主,也就是说你不能比对手猛,你骗倒对手也行,比如桃花岛的落英神剑掌:
这套掌法是黄药师观赏桃花岛中桃花落英缤纷而创制,出招变化多端,还讲究姿势之美。她双臂挥动,四方八面都是掌影,或五虚一实,或八虚一实,直似桃林中狂风忽起、万花齐落,妙在手足飘逸,宛若翩翩起舞,但她一来功力尚浅,二来心存顾惜,未能出掌凌厉如剑。郭靖眼花缭乱,哪里还守得住门户,不提防啪啪啪啪,左肩右肩、前胸后背,接连中了四掌,黄蓉全未使力,郭靖自也不觉疼痛。
——出自《射雕英雄传》世纪新修版
第三种是以巧招为主,它不求一味刚猛,也不一味虚虚实实,而且讲究用力恰到好处,起到“以柔克刚”、“四两拨千斤”之效。显然,这种武功的代表作是太极,另外打狗棒法、乾坤大挪移、还有全真教和古墓派的武功也暗含了这个道理,比如:
杨过在危急中使了一招全真派剑法,居然收到奇效,跟着又是一招全真派的“白虹经天”,平剑旋转向轮子打去。轮重剑轻,这一剑平击本无效用,但这一下旋转恰到好处,合上了武学中“四两拨千斤”的道理,铁轮方向转过,反向国师头上飞去。
——出自《神雕侠侣》世纪新修版
“四两拨千斤”的说法,在很多文学作品都出现过。很多读者应该都认为,四两拨千斤只不过是小说中的夸张手法,事实上是不可能的,也有的人觉得古人的“武功”只不过是失传了,古代是真实存在的。这里我们从物理学的角度分析一下四两拨千斤的可能性,给出一个另类的读金庸的例子。
物理学 #
事实上,“四两拨千斤”的基本原理就是不要“硬碰硬”,所谓不要硬碰硬,就是你的发力要跟来力垂直,这样(理论上)我们就不受到来力的冲击。当然,这还不够。作为最基本的分析,我们可以将问题简化为:
一个大质量物体在做匀速直线运动(一股大力向我们袭来),然后某时刻开始受到大小恒定的力(也就是我们能使出的力)的作用,并且这个力保持跟物体本身的速度方向保持垂直,求物体的运动轨迹(看我们能不能避开这个攻击)。
我们还可以进一步简化,为了分析的方便,假设仅仅是在平面运动。分析的要点在于描述“力的方向与速度方向垂直”,我们知道,描述角度关系,用复数是最适合的,于是我们可以假设用一个复函数$z\equiv z(t)$来描述运动轨迹,并且设恒力大小为$f$,那么可以列出运动方程为:
$$m\ddot{z}=f\frac{\dot{z}}{|\dot{z}|}e^{i\pi/2}$$
为了求解这个方程,首先可以设$\dot{z}=re^{i\theta}$,那么就有
$$m\frac{d}{dt}(re^{i\theta})=fe^{i(\theta+\pi/2)}$$
展开得到
$$m\dot{r}e^{i\theta}+mir\dot{\theta}e^{i\theta}=fe^{i(\theta+\pi/2)}$$
复数的神奇之处就是:现在我们可以两边消去$e^{i\theta}$了:
$$m\dot{r}+mir\dot{\theta}=fe^{i\pi/2}$$
根据实部和虚部分别相等的原则,我们可以得到
$$\begin{aligned}&m\dot{r}=0\\
&mr\dot{\theta}=f\end{aligned}$$
那么很显然:
$$r \equiv v_0,\quad \theta=\theta_0+\frac{f}{mv_0}t$$
注意$re^{i\theta}$描述的是$\dot{z}$,也就是速度,所以上式告诉我们,速度大小不变,速度方向匀速变化,这是一个“匀速圆周运动”!当然,不通过求解微分方程的方式,也可以得到上述结果,这里是为了给出一般的分析过程,以便有兴趣的读者可以参照来分析更复杂的过程。
现在通过旋转坐标轴,所以由
$$\dot{z}=v_0\exp \left(i\theta_0 + i\frac{ft}{mv_0}\right)$$
积分得到
$$z(t)=z_0 + \frac{mv_0^2 e^{i\theta_0}}{if}\left[\exp\left(i\frac{ft}{mv_0}\right)-1\right]$$
由于出拳方向是“袭击”我们,因此可以取$\theta_0=\pi$,得到
$$z(t)=z_0 + \frac{imv_0^2}{f}\left[\exp\left(i\frac{ft}{mv_0}\right)-1\right]$$
或者分解开来看,那就是
$$\begin{aligned}x =& x_0 - \frac{mv_0^2}{f}\sin\left(\theta_0 + \frac{ft}{mv_0}\right)\\
y =& y_0 + \frac{mv_0^2}{f}\left[\cos\left(\theta_0 + \frac{ft}{mv_0}\right)-1\right]
\end{aligned}$$
实际情况 #
既然最后求解的轨迹是一个匀速圆周运动,是圆!于是就不难理解《倚天屠龙记》一段话了:
张无忌的一柄木剑在这团寒光中画着一个个圆圈,每一招均以弧形刺出,以弧形收回,他心中竟没半点渣滓,以意运剑,木剑每发一招,便似放出一条细丝,去缠在倚天宝剑之上,细丝越积越多,似乎积成了一团团丝棉,将倚天剑裹了起来。
...
张无忌却始终持剑画圆,旁人除张三丰外,没一个瞧得出他每一招到底是攻是守。这路太极剑法只是大大小小、正反斜直各种各样的圆圈,要说招数,可说便只一招,然而这一招却永远出没无穷。
————出自《倚天屠龙记》世纪新修版
因此,从物理学的角度我们可以知道,太极的要诀顺着来力的方向画圆,这就是“粘”字诀,而且要保持垂直,显然太极是很有技巧的。有读者就疑问了,如果张无忌没有学过九阳神功,内力不深,那还有可能“拨千斤”吗?
我们来一个更加较真的例子,数据来源于《“四两拨千斤”可能吗?——“四两拨千斤”的物理学分析》:
以被击打者(施太极的人)为原点,假设手臂重量$m=6\mbox{kg}$,出拳速度$v_0=7\mbox{m/s}$,设$(x_0,y_0)=( 0.5\mbox{m},0)$,0.5米大概就是我们开始向对方发力的地方。这样就有
$$\begin{aligned}x =&\, 0.5 - \frac{294}{f}\sin\left(\frac{ft}{42}\right)\\
y =&\, \frac{294}{f}\left[\cos\left(\frac{ft}{42}\right)-1\right]
\end{aligned}$$
当对手击中我们时,$x=0$,那么
$$\sin\left(\frac{ft}{42}\right)=\frac{f}{588}$$
从而
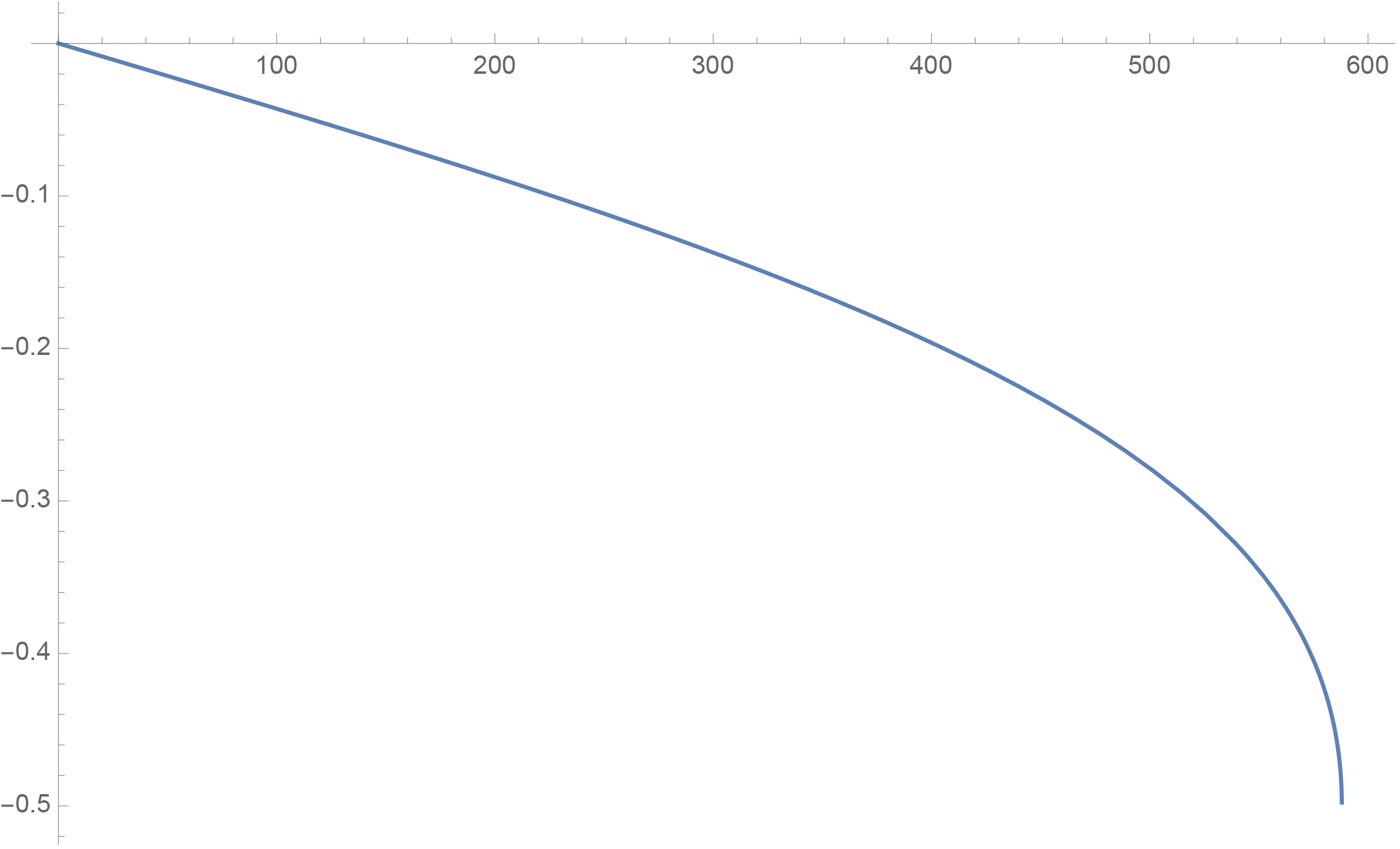
$$y = \frac{294}{f}\left[\sqrt{1-\left(\frac{f}{588}\right)^2}-1\right]$$
如果身体的宽度是$d_{min}$,那么就至少要$y > d_{min}$,考虑到这是超越方程,因此用数值求解即可。
假如要躲避头部攻击,那么可以考虑$d_{min}=0.1\mbox{m}$,那么从图上可以看出这时候要$f=250\mbox{N}$左右。这个力是什么概念?根据《“四两拨千斤”可能吗?——“四两拨千斤”的物理学分析》的分析,普通拳师的出拳力量也不过是这个量级!如果要躲避身体攻击,那么可以考虑$d_{min}=0.25\mbox{m}$,那么这时候要$f=500\mbox{N}$左右!这是很有可能已经超过了普通拳师的出拳力量了。
当然,这是很机械的分析,实际上我们也有可能灵活闪避,不可能纯推,好比电影《太极1》里边的台词“一抓 一带 一勾 一穿 打的俺上天入地”。但这个分析已经足够表明,单靠“拨”的话,“四两拨千斤”是不可能的。
最后 #
看来,太极拳还是跟九阳神功更配哦,没有九阳神功的功底,怕是很难用太极对打了。似乎还是乾坤大挪移的见解高明一点:
乾坤大挪移神功较浅近的一二层,类似于“四两拨千斤”之法,但到了较高层次,反过来变成了“千斤拨四两”,以近乎千斤的浩浩内力,去拨动对手小小的劲力,似乎是“杀鸡用牛刀”,但正因用的是“牛刀”,杀此鸡便轻而易举了。
————出自《倚天屠龙记》世纪新修版
那如果有九阳神功的功力了呢?读者可能会困惑,九阳神经已经够猛了,足够对敌,为啥还要多此一举练个太极?现在看来,太极的特点不是省力,而是减少对自身的伤害。试想,两个拳头硬碰硬地相撞,那是多么疼的领悟啊!如果避其锋芒,采用太极的画圆侧推方式,那么对自身的伤害是最小的。
(其实我对拳术一无所知,以上纯粹是茶余饭后的谈资,博读者一笑~)。
转载到请包括本文地址:https://kexue.fm/archives/5048
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Jan. 28, 2018). 《【理科生读小说】来谈谈“四两拨千斤” 》[Blog post]. Retrieved from https://kexue.fm/archives/5048
@online{kexuefm-5048,
title={【理科生读小说】来谈谈“四两拨千斤”},
author={苏剑林},
year={2018},
month={Jan},
url={\url{https://kexue.fm/archives/5048}},
}










January 28th, 2018
哈哈哈哈哈哈哈哈哈哈哈哈
January 15th, 2021
搂主,公式是怎么输入进去的?
mathjax+latex,很成熟的方案了。