从费马大定理谈起（十一）：有理点与切割线法

我们在这个系列的文章之中，探索了一些有关环和域的基本知识，并用整环以及唯一分解性定理证明了费马大定理在n=3和n=4时的情形。使用高斯整数环或者艾森斯坦整数环的相关知识，相对而言是属于近代的比较“高端”的代数内容（高斯生于1777年，艾森斯坦生于1823年，然而艾森斯坦英年早逝，只活到了1852年，高斯还活到了1855年。）。如果“顺利”的话，我们可以用这些“高端”的工具证明解的不存在性，或者求出通解（如果有解的话）。

然而，对于初等数论来讲，复数环和域的知识的门槛还是有点高了。其次，环和域是一个比较“强”的工具。这里的“强”有点“强势”的意味，是指这样的意思：如果它成功的话，它能够“一举破城”，把通解都求出来（或者证明解的不存在）；如果它不成功的话，那么往往就连一点非平凡的解都求不出来。可是，有些问题是求出一部分解都已经很困难了，更不用说求出通解了（我们以后在研究$x^4+y^4 = z^4 + w^4 $的整数解的时候，就能深刻体会这点。）。因此，对于这些问题，单纯用环域的思想，很难给予我们（至少一部分）解。（当然，问题是如何才算是“单纯”，这也很难界定。这里的评论是比较粗糙的。）

而本文要介绍的，则是一种几何式的方法，它可以有效地帮助我们求出某些不定方程的有理点。让人惊奇的是，这个方法不算新颖，甚至已经很“古老”了，因为根据考究，“不定方程之祖”——丢番图就用过它。它是一种求曲线上的有理点的几何技巧。正如我们所看到的，很多不定方程的整数解问题，都可以转化为相应的有理数解问题，于是这个方法也就奏效了。事不宜迟，我们来看看这种方法。（本文的思想来自于《数学及其历史》。）

圆上的有理点 #

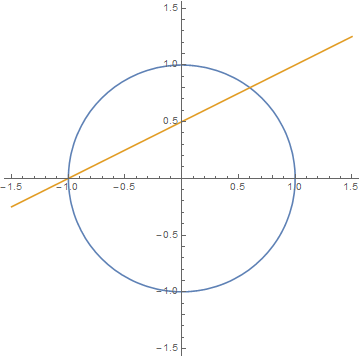
首先是割线法，笔者觉得介绍割线法的最好例子，当属勾股数问题了。求不定方程$a^2+b^2=c^2$的整数解，可以等价地求单位圆$x^2+y^2=1$上的有理点问题。而显然的有理点是$(\pm 1,0)$，割线法的目的，就是根据这些显然的有理点，求出一族非平凡的有理点来。其中的思想也不算困难，主要是利用了代数方程的根与系数的关系——韦达定理！

我们过点$(-1,0)$作一条斜率为$k$的直线，其方程为
$$y=k(x+1)$$
该直线已经和圆$x^2+y^2=1$交于$(-1)$，那么它必然跟单位圆有另外一个交点，现在要考虑的问题是：另外一个交点是不是有理点呢？根据韦达定理，不难发现只要$k$是一个有理数，那么另外一个交点必然也是有理点。这是因为将直线方程代进去后，得到一道一元二次方程
$$1=x^2+k^2 (x+1)^2=(1+k^2)x^2 + 2k^2 x +k^2$$
只要$k$是有理数，那么方程的系数都是有理数，根据韦达定理，$x_1 + x_2=-\frac{2k^2}{1+k^2}$，一个根是$x_1=-1$，那么另外一个根必然也有有理数，为$x_2=\frac{1-k^2}{1+k^2}$，因而另外一个点便是有理点$\left(\frac{1-k^2}{1+k^2},\frac{2k}{1+k^2}\right)$了。稍加整理，就可以从中得到勾股数组的通式。

三次曲线上的有理点 #

我们之前考虑过$x^3+y^3=z^3+w^3$的整数解问题，我们将它看成是关于$x,y$的方程，它是三次的，$z,w$是有理参数，那么它有一个平凡的有理点$(x,y) = (z,w)$。

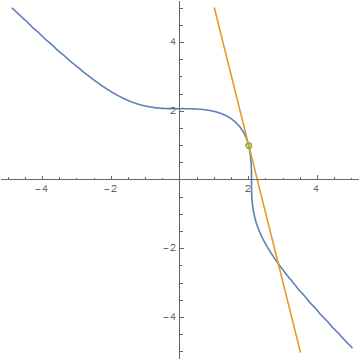
类比圆上有理点的求法，如果已知三次曲线上的两个有理点，那么过这两个有理点作一条割线，跟三次曲线交于第三点，那么第三点必然也是有理点。然而，大多数情况是，我们只能知道方程的一个有理点。因此有没有办法只根据一个有理点求出其他的有理点呢？办法还是有的，我们让已知的那两个有理点无限重合，于是割线也就成了切线——换句话说，已知一个有理点，然后在这个有理点处作原曲线的切线，联立切线和原曲线的方程，得到一道有理系数的一元三次方程。这时，已知的那个有理点是三次方程的二重根！那么剩下的第三个根，必然是有理的。下面以求$x^3+y^3=z^3+w^3$的一族解为例，具体展示切线法的技巧。

通过两边求导，可以得到：
$$3 x^2+ 3 y^2 \frac{dy}{dx}=0$$
也就可以求出在点$(z,w)$处有$\frac{dy}{dx}=-\frac{z^2}{w^2}$，继而过该点的切线方程是
$$y=-\frac{z^2}{w^2}(x-z)+w$$
代进原方程则有
$$x^3+\left[-\frac{z^2}{w^2}(x-z)+w\right]^3=z^3+w^3$$
求得第三个根为（两个重根是$w=z$）
$$x=\frac{2 w^3 z+z^4}{z^3-w^3}$$
对应地
$$y=\frac{w^4+2 w z^3}{w^3-z^3}$$
因此我们求出了一个二参数的有理数解
$$\left(\frac{2 w^3 z+z^4}{z^3-w^3}\right)^3+\left(\frac{w^4+2 w z^3}{w^3-z^3}\right)^3=z^3+w^3$$
当然，这个参数解并不能生成所有的有理数解，这从它的二参数可以看出：完整的有理数解至少包含三参数。这是切线法的特点：它通常是有效的，但却是不完全的。很多三次曲线问题都可以类似地求出一族有理解来（前提当然是它有有理解，至少得知道一组特殊的有理解），更具一般性的方程是$y^2=ax^3+bx^2+cx+d$，其中$a,b,c,d$都是有理数。

y²=ax³+bx²+cx+d的切线结果 #

为了方便后面的应用，这里我们不加推导地给出$y^2=ax^3+bx^2+cx+d$的结果。有兴趣的朋友可以自行推导，方法跟上面是一样的，只是步骤多了一点，复杂度基本没变；或者参考文末的参考书籍。已知该三次曲线过$(x_1,y_1)$和$(x_2,y_2)$，那么用割线法求得第三个点为
$$x_3=-(x_1 + x_2)-\frac{b-[(y_2-y_1)/(x_2-x_1)]^2}{a}$$
考虑只有一个点$(x_1,y_1)$的情况，也就是将$\frac{y_2-y_1}{x_2-x_1}$换成在该点处的导数$\frac{dy}{dx}$，也就是
$$\left\{\begin{aligned}&\frac{dy}{dx}=\frac{3ax_1^2+2bx_1+c}{2y_1}\\
&x_2=-2 x_1-\frac{b-[(3ax_1^2+2bx_1+c)/(2y_1)]^2}{a}\end{aligned}\right.$$

莫德尔定理 #

我们通过切线法求出了三次曲线的一批有理点，接下来我们可以施行两个步骤：

1、以这些新的有理点为切点，作切线，然后可以求出另外的一批解；
2、任意选两个有理点，作割线，也可以求出新的有理点。

这两个步骤可以不断重复做下去。问题是，这样我们能得到所有的有理数点吗？

答案是肯定的，这是由庞加莱提出猜想、并由莫德尔（Mordell）所证明的：所有的有理点可以经有限多个点的切线和弦的作图所生成。这再次肯定了切割线法的价值。当然，我们目前还不知道一般化的通过切线、割线的方式得到全体有理点的算法。

谈谈丢番图 #

很难想象上述技巧出现在差不多两千年前，但事实应该如此！

古希腊亚历山大学后期的重要学者和数学家丢番图（Diophantus）（约公元246—330年，据推断和计算而知）在他的著作《算术》（Arithmetica）中，讨论过很多二次曲线和三次曲线上的有理点问题，但是他的方法并没有流传下来。一千多年后，费马也研究过曲线的有理点和整点的问题，并给出了一些断论（或者说是猜想），但费马的研究方法也没有流传开来。而跟费马差不多同一时代的微积分创始人牛顿，则给出了割线法和切线法，并且认为丢番图和费马所用的方法就是切割线法。我们今天是相信这一猜测的，因为不管怎么看，我们求代数曲线上的有理点的其他方法，都比切割线法要“高端”，相对而言，切割线法就是很“平民化”的工具了。其次，古希腊热衷于几何研究，最终得到了切割线法来研究有理点问题，也是很有可能的。

参考书籍 #

《数学及其历史》，作者：John Stillwell，出版社：高等教育出版社

转载到请包括本文地址：https://kexue.fm/archives/2996

更详细的转载事宜请参考：《科学空间FAQ》