七月再次“农忙”，农村里要插秧了，播下种苗，等待再次收获的季节^_^

我一直觉得我的数学能力偏向于分析计算而不擅长于几何，纵使遇到几何问题，也是满脑子的解析几何做法，没有纯几何的美。而这几天为了加强数学竞赛题目的能力，我一直在看IMO的题目，并且企图独立做出一些题目，但都无果。我比较感兴趣的是不等式，我感觉一道简单的式子，不用太多的文字就可以讲清楚的题目非不等式莫属，但是IMO的不等式题实在高深，我还没有能够独立做出一道来（参考答案可以看懂，只是想不到思路），或许是我在努力追求统一的方法而不肯研究那些特定的技巧的原因吧。不料今天看了一下2001年IMO的几何题目，发现我可能将它做出来，于是研究了一会，最终很幸运地做了出来。虽然不是最简单的方法，但也与大家分享一下。

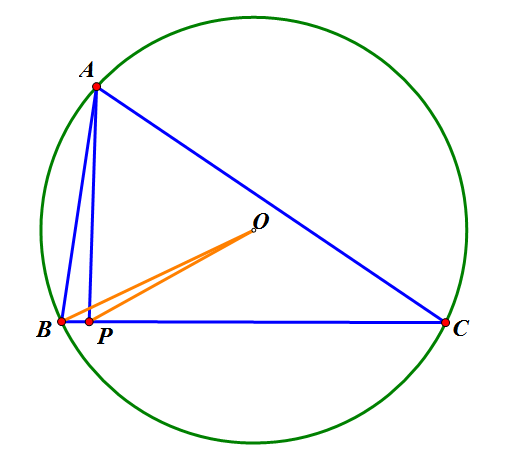
IMO-42-1

IMO-42-1

如图，O是锐角三角形ABC的外心，AP是三角形的垂线段，∠B-∠C不小于30°。证明∠BAC+∠BOP < 90°

其实BoJone能做出这道题，是因为这道题目着实不难。我的几何水平依旧停留在初中的阶段，我的证明依旧着重于分析和计算。首先由“∠B-∠C不小于30°”可以得出∠B > 60°和∠A+∠C < 120°，不然会得出∠C是直角或钝角的结果，这与题目矛盾。

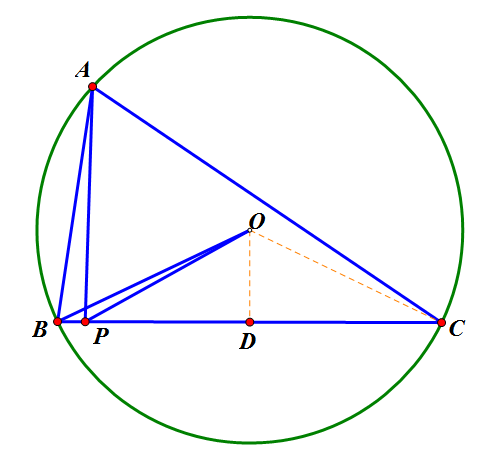
按下图作辅助线：OD垂直于BC，连接O、C，三角形的三个角直接记为A、B、C。

IMO-42-1-解答

IMO-42-1-解答

由圆心角是对应圆周角的两倍可以得出：∠BOC=2∠A，于是∠A=∠BOD，题目要证∠A+∠BOP < 90°，即证∠BOD+∠BOP < 90°，而∠BOD+∠OBD=90°，等价于证明∠BOP < ∠OBD，亦等价于证明BP < OP，即BP2 < OP2。

设角A、B、C的对边分别为a,b,c，外接圆半径为R，不难看出：
$$BP=c\cdot \cos B$$
由余弦定理：
$$\begin{aligned}OP^2=BP^2+R^2-2R\cdot BP\cdot \cos \angle OBD \\ =BP^2+R^2-2R\cdot BP\cdot \sin \angle BOD=BP^2+R^2-2R\cdot c\cdot \cos B\cdot \sin A\end{aligned}$$

于是证明的结论变为：$R^2-2R*c*cosB*sin A > 0$，而由正弦定理知道：$2R*sin C=c$，所以最终要证明：
$$4\sin A\cdot \sin C\cdot \cos B < 1$$

积化和差：$sin C cos B=1/2 [sin(B+C)-sin(B-C)]$，B-C ≥ 30°，所以 \sin(B-C) ≥ 1/2

因此：
$$\begin{aligned}4\sin A\cdot \sin C\cdot \cos B =2 \sin A [\sin(B+C)-\sin(B-C)] \\ < 2 \sin A (\sin A-1/2) \leq 2\cdot 1\cdot (1-1/2)=1\end{aligned}$$

证毕。

本文的证明方法属于杀鸡用牛刀...只是BoJone的几何能力实在太弱，不能想出更好的证明方法...

转载到请包括本文地址：https://kexue.fm/archives/1453

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (Jul. 30, 2011). 《IMO42-1，我也会做几何题 》[Blog post]. Retrieved from https://kexue.fm/archives/1453

@online{kexuefm-1453,
        title={IMO42-1，我也会做几何题},
        author={苏剑林},
        year={2011},
        month={Jul},
        url={\url{https://kexue.fm/archives/1453}},
}