这已经是去年写的稿件了，刊登在今年二月份的《天文爱好者》上，本文的标题还登载了该期天爱的封面上，当时甚是高兴呢！在此与大家分享、共勉。
相信许多天文爱好者都知道第一、第二、第三宇宙速度的概念，也会有不少的天爱自己动手计算过它们。我们道，只要发射速度达到7.9km/s，宇宙飞船就可以绕地球运行了；超过11.2km/s，就可以抛开地球，成为太阳系的一颗“人造行星”；再大一点，超过16.7km/s，那么就连太阳也甩掉了，直奔深空。
16.7km/s，咋看上去并不大，因为地球绕太阳运行的速度已经是30km/s了，这个速度在宇宙中实在是太普通了。但是对于我们目前的技术来说，它大得有点可怕。维基百科上的资料显示，史上最强劲的火箭土星五号在运送阿波罗11号到月球时，飞船最终也只能加速到接近逃逸速度，即11.2km/s，而事实上第三宇宙速度已经是是目前人造飞行器的速度极限了。可是没有速度，我们就不能发射探测器去探索深空，那些科幻小说中的“星际移民”，就永远只能停留在小说上了。
在天文爱好者眼中，黑洞是一个球体，其半径为$\frac{2GM}{c^2}$；这是广义相对论的施瓦兹黑洞的结果，也从经典力学推导推导出来，虽然用经典力学是错误的，但是对于多数的天文爱好者（包括笔者）来说，这是目前唯一的一种可行的理解方法（广义相对论那些复杂推导会让我们很崩溃的）。当然，事实上，黑洞不是一个球体，它只是一个密度很大的点。至于密度有多大，目前公认的说法是无穷大，但是严格的物理是不接受这个说法的，或者说，物理是不会接受任何无穷大的说法，所以现在积极发展量子引力理论来统一相对论和量子力学，不过这是另话了。$\frac{2GM}{c^2}$只不过是黑洞的视界，视界之内，我们就什么也不知道了。本文主要就从经典力学的角度探讨一下两个黑洞的合并过程中其视界的变化。读者将会发现，这些视界的形状相当有趣。
经典力学中的黑洞是这样定义的：天体表面的逃逸速度超过了光速，于是连光都无法逃脱，所以这个“洞”就很黑。也就是说，光子的总能量（引力势能与动能之和，经典力学意义下的）要为负，负数表示受到束缚。用数学公式来讲，就是：
$$\frac{1}{2}mc^2 - \frac{GM_1 m}{r_1}-\frac{GM_2 m}{r_2}-...-\frac{GM_n m}{r_n} \leq 0$$
16
Nov
天体力学巨匠——拉普拉斯
By 苏剑林 | 2012-11-16 | 39124位读者 | 引用本文其实好几个月前就已经写好了，讲的是我最感兴趣的天体力学领域的故事，已经发表在2012年11月的《天文爱好者》上。
天体力学巨匠——拉普拉斯
作为一本天文科普杂志，《天文爱好者》着眼于普及天文，内容偏向于有趣的天体物理等，比较少涉及到天体力学。事实上，在天文发展史中，天体力学——研究天体纯粹在万有引力作用下演化的科学——占据了相当重要的地位。过去，天文就被划分为天体力学、天体物理以及天体测量学三个大块。只是在近现代，由于电子计算机的飞速发展，天体力学的多数问题都交给了计算机数值计算解决，因此这一领域逐渐淡出了人们视野。不过，回味当初那段天体力学史，依然让我们觉得激动人心。
首先引入“天体力学（Celestial mechanics）”这一术语的是法国著名数学家、天文巨匠拉普拉斯。他的全名为皮埃尔?西蒙?拉普拉斯（Pierre?Simon marquis de Laplace），因研究太阳系稳定性的动力学问题被誉为法国的牛顿和天体力学之父。他和生活在同一时代的法国著名数学家拉格朗日以及勒让德（Adrien-Marie Legendre）并称为“三L”。
神秘的少年时期
由于1925年的一场大火，很多拉普拉斯的生活细节资料都丢失了。根据W. W. Rouse Ball的说法，他可能是一个普通农民或农场工人的儿子，1749年3月23日出生于诺曼底卡尔瓦多斯省的伯蒙特恩奥格。少年时期，拉普拉斯凭借着自己的才能和热情，在富人邻居的帮助下完成了学业。他父亲希望这能使他将来以宗教为业，16岁时，他被送往卡昂大学读神学。但他很快在数学上显露头角。
13
Jan
混沌的世界——“星之轨迹”的研究
By 苏剑林 | 2012-01-13 | 33343位读者 | 引用（本文已被刊登在2012年1月的《天文爱好者》上，于笔者而言这是一份很棒的新年礼物！）
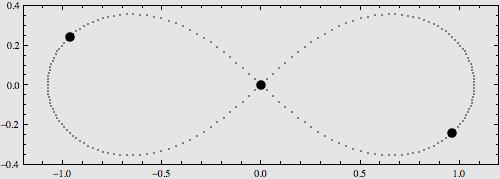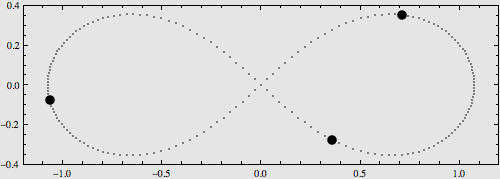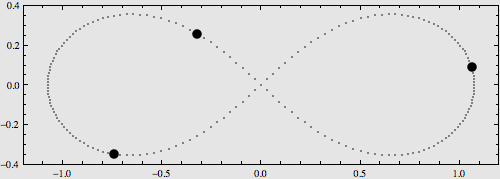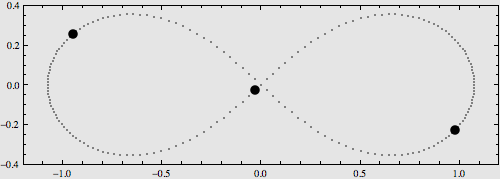
在去年第七期《天爱》上，我们看到了N体问题所呈现出来的一些对称、漂亮的周期轨道，这体现了N体问题和谐有序的一面。但是这仅仅是N体问题的冰山一角，笔者也提到过N体问题的本质是混沌、无序的，通俗来讲就是非常乱，无法用数学方程来精确描述。这看起来是一种不完美。但试想，探索当初伽利略将望远镜对准月球后，看到的是如想象中光滑的月面，那么他还会惊叹宇宙的神奇吗？
本文就让我们来更深入地了解一下N体问题的研究历史。
观测&拟合时代
由于人类的自我优越感以及日月星辰东升西落的经验，让我们长期都认为地球是宇宙的中心。第一个比较系统提出地心说的人当属天文学家欧多克斯（Eudoxus，死于公元前347年左右），但他的地心说是非常粗糙的，以至于无法解释很多基本现象，如无法准确预言日食和解释行星逆行等。但亚里士多德接受了地心说，并且由于他在政治和科学上的权威，使地心说免去了夭折的命运。后来托勒密通过他的本轮，完善了地心说，使之延续到了16世纪。
19
Dec
N体问题的30个周期性解
By 苏剑林 | 2010-12-19 | 47013位读者 | 引用
16
Aug
《方程与宇宙》:拉格朗日点,复数,向量(五)
By 苏剑林 | 2010-08-16 | 43815位读者 | 引用The New Calculation Of Lagrangian Point 4,5
上一回我们已经求出了拉格朗日点L1,L2,L3，并且希望能够求出L4,L5两个点。由于L4,L5与“地球-太阳”连线已经不共线了，所以前边的方法貌似不能够用了。为了得到一个通用的定义，我们可以采用以下方法来描述拉格朗日点：位于拉格朗日点的天体，它与太阳的连线以及地球与太阳的连线所组成的角的大小是恒定的。（这里为了方便，采用了地日系的拉格朗日点来描述，对于一般的三体问题是一样的）
对于L4,L5来说，我们或许可以设置一个新的向量来描述这两点的向径（如$\vec{R}$）。当我们这样做后，很快就会发现这样会令我们的计算走向死胡同。因为我们发现：已知两个向量的夹角和其中一个向量，我们很难把另一个向量用已知向量的式子表达出来。不能做到这一点，就不能找出$\vec{R}$与$\vec{r}$的关系，就无法联立方程求解。难道，我们这一条路走到尽头了吗？一开始BoJone也冥思苦想不得头绪，但是...
15
Aug
《方程与宇宙》:拉格朗日点的点点滴滴(四)
By 苏剑林 | 2010-08-15 | 79795位读者 | 引用The New Calculation Of Lagrangian Point 1,2,3
L2_rendering
关于n体问题，选择质心或其他定点为参考点，我们可以列出下面的运动方程：
$$\ddot{\vec{r}}_k=\sum_{i=1,i != k}^{n} Gm_i\frac{\vec{r}_i-\vec{r}_k}{|\vec{r}_i-\vec{r}_k|^3}\tag{19}$$
现在我们只考虑三体问题。天文学家一直希望能够找到三体问题的简洁解，可是很遗憾，庞加莱已经证明了三体问题的解是混沌的，也就是说任何微小的扰动都有可能造成不可预料的后果（可以形象的比喻为：巴西的一只蝴蝶翅膀的扇动，有可能因此美国的一场龙卷风）。
最近评论