多任务学习漫谈(一):以损失之名
By 苏剑林 | 2022-01-18 | 156957位读者 | 引用能提升模型性能的方法有很多,多任务学习(Multi-Task Learning)也是其中一种。简单来说,多任务学习是希望将多个相关的任务共同训练,希望不同任务之间能够相互补充和促进,从而获得单任务上更好的效果(准确率、鲁棒性等)。然而,多任务学习并不是所有任务堆起来就能生效那么简单,如何平衡每个任务的训练,使得各个任务都尽量获得有益的提升,依然是值得研究的课题。
最近,笔者机缘巧合之下,也进行了一些多任务学习的尝试,借机也学习了相关内容,在此挑部分结果与大家交流和讨论。
加权求和
从损失函数的层面看,多任务学习就是有多个损失函数$\mathcal{L}_1,\mathcal{L}_2,\cdots,\mathcal{L}_n$,一般情况下它们有大量的共享参数、少量的独立参数,而我们的目标是让每个损失函数都尽可能地小。为此,我们引入权重$\alpha_1,\alpha_2,\cdots,\alpha_n\geq 0$,通过加权求和的方式将它转化为如下损失函数的单任务学习
\begin{equation}\mathcal{L} = \sum_{i=1}^n \alpha_i \mathcal{L}_i\label{eq:w-loss}\end{equation}
在这个视角下,多任务学习的主要难点就是如何确定各个$\alpha_i$了。
多任务学习漫谈(二):行梯度之事
By 苏剑林 | 2022-02-08 | 53389位读者 | 引用在《多任务学习漫谈(一):以损失之名》中,我们从损失函数的角度初步探讨了多任务学习问题,最终发现如果想要结果同时具有缩放不变性和平移不变性,那么用梯度的模长倒数作为任务的权重是一个比较简单的选择。我们继而分析了,该设计等价于将每个任务的梯度单独进行归一化后再相加,这意味着多任务的“战场”从损失函数转移到了梯度之上:看似在设计损失函数,实则在设计更好的梯度,所谓“以损失之名,行梯度之事”。
那么,更好的梯度有什么标准呢?如何设计出更好的梯度呢?本文我们就从梯度的视角来理解多任务学习,试图直接从设计梯度的思路出发构建多任务学习算法。
整体思路
我们知道,对于单任务学习,常用的优化方法就是梯度下降,那么它是怎么推导的呢?同样的思路能不能直接用于多任务学习呢?这便是这一节要回答的问题。
Efficient GlobalPointer:少点参数,多点效果
By 苏剑林 | 2022-01-25 | 124063位读者 | 引用在《GlobalPointer:用统一的方式处理嵌套和非嵌套NER》中,我们提出了名为“GlobalPointer”的token-pair识别模块,当它用于NER时,能统一处理嵌套和非嵌套任务,并在非嵌套场景有着比CRF更快的速度和不逊色于CRF的效果。换言之,就目前的实验结果来看,至少在NER场景,我们可以放心地将CRF替换为GlobalPointer,而不用担心效果和速度上的损失。
在这篇文章中,我们提出GlobalPointer的一个改进版——Efficient GlobalPointer,它主要针对原GlobalPointer参数利用率不高的问题进行改进,明显降低了GlobalPointer的参数量。更有趣的是,多个任务的实验结果显示,参数量更少的Efficient GlobalPointer反而还取得更好的效果。
大量的参数
这里简单回顾一下GlobalPointer,详细介绍则请读者阅读《GlobalPointer:用统一的方式处理嵌套和非嵌套NER》。简单来说,GlobalPointer是基于内积的token-pair识别模块,它可以用于NER场景,因为对于NER来说我们只需要把每一类实体的“(首, 尾)”这样的token-pair识别出来就行了。
GPLinker:基于GlobalPointer的实体关系联合抽取
By 苏剑林 | 2022-01-30 | 121330位读者 | 引用在将近三年前的百度“2019语言与智能技术竞赛”(下称LIC2019)中,笔者提出了一个新的关系抽取模型(参考《基于DGCNN和概率图的轻量级信息抽取模型》),后被进一步发表和命名为“CasRel”,算是当时关系抽取的SOTA。然而,CasRel提出时笔者其实也是首次接触该领域,所以现在看来CasRel仍有诸多不完善之处,笔者后面也有想过要进一步完善它,但也没想到特别好的设计。
后来,笔者提出了GlobalPointer以及近日的Efficient GlobalPointer,感觉有足够的“材料”来构建新的关系抽取模型了。于是笔者从概率图思想出发,参考了CasRel之后的一些SOTA设计,最终得到了一版类似TPLinker的模型。
基础思路
关系抽取乍看之下是三元组$(s,p,o)$(即subject, predicate, object)的抽取,但落到具体实现上,它实际是“五元组”$(s_h,s_t,p,o_h,o_t)$的抽取,其中$s_h,s_t$分别是$s$的首、尾位置,而$o_h,o_t$则分别是$o$的首、尾位置。
指数梯度下降 + 元学习 = 自适应学习率
By 苏剑林 | 2022-03-03 | 31539位读者 | 引用前两天刷到了Google的一篇论文《Step-size Adaptation Using Exponentiated Gradient Updates》,在其中学到了一些新的概念,所以在此记录分享一下。主要的内容有两个,一是非负优化的指数梯度下降,二是基于元学习思想的学习率调整算法,两者都颇有意思,有兴趣的读者也可以了解一下。
指数梯度下降
梯度下降大家可能听说得多了,指的是对于无约束函数$\mathcal{L}(\boldsymbol{\theta})$的最小化,我们用如下格式进行更新:
\begin{equation}\boldsymbol{\theta}_{t+1} = \boldsymbol{\theta}_t - \eta\nabla_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta}_t)\end{equation}
其中$\eta$是学习率。然而很多任务并非总是无约束的,对于最简单的非负约束,我们可以改为如下格式更新:
\begin{equation}\boldsymbol{\theta}_{t+1} = \boldsymbol{\theta}_t \odot \exp\left(- \eta\nabla_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta}_t)\right)\label{eq:egd}\end{equation}
这里的$\odot$是逐位对应相乘(Hadamard积)。容易看到,只要初始化的$\boldsymbol{\theta}_0$是非负的,那么在整个更新过程中$\boldsymbol{\theta}_t$都会保持非负,这就是用于非负约束优化的“指数梯度下降”。
多任务学习漫谈(三):分主次之序
By 苏剑林 | 2022-02-14 | 36392位读者 | 引用多任务学习是一个很宽泛的命题,不同场景下多任务学习的目标不尽相同。在《多任务学习漫谈(一):以损失之名》和《多任务学习漫谈(二):行梯度之事》中,我们将多任务学习的目标理解为“做好每一个任务”,具体表现是“尽量平等地处理每一个任务”,我们可以称之为“平行型多任务学习”。然而,并不是所有多任务学习的目标都是如此,在很多场景下,我们主要还是想学好某一个主任务,其余任务都只是辅助,希望通过增加其他任务的学习来提升主任务的效果罢了,此类场景我们可以称为“主次型多任务学习”。
在这个背景下,如果还是沿用平行型多任务学习的“做好每一个任务”的学习方案,那么就可能会明显降低主任务的效果了。所以本文继续沿着“行梯度之事”的想法,探索主次型多任务学习的训练方案。
目标形式
在这篇文章中,我们假设读者已经阅读并且基本理解《多任务学习漫谈(二):行梯度之事》里边的思想和方法,那么在梯度视角下,让某个损失函数保持下降的必要条件是更新量与其梯度夹角至少大于90度,这是贯穿全文的设计思想。
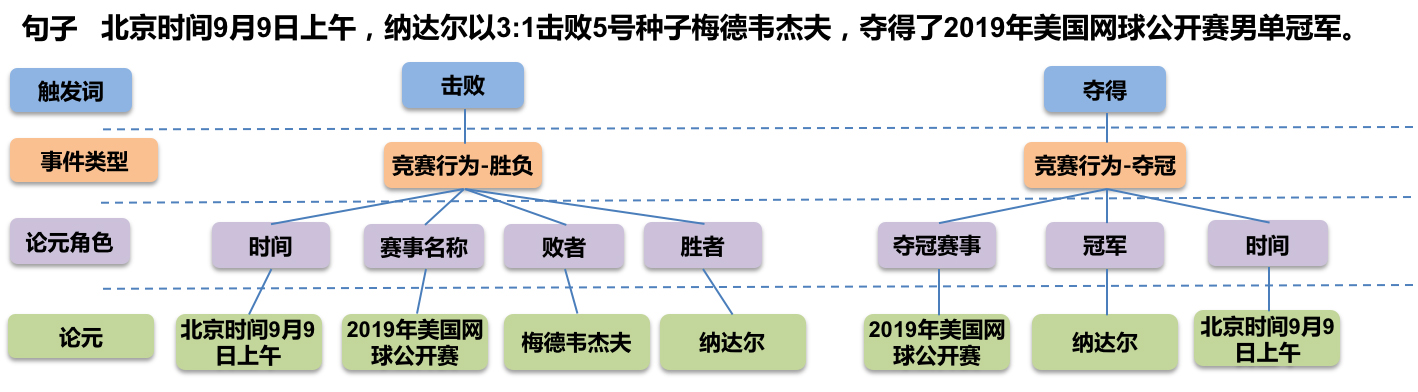
GPLinker:基于GlobalPointer的事件联合抽取
By 苏剑林 | 2022-02-21 | 78716位读者 | 引用大约两年前,笔者在百度的“2020语言与智能技术竞赛”中首次接触到了事件抽取任务,并在文章《bert4keras在手,baseline我有:百度LIC2020》中分享了一个转化为BERT+CRF做NER的简单baseline。不过,当时的baseline更像是一个用来凑数的半成品,算不上一个完整的事件抽取模型。而这两年来,关系抽取的模型层见迭出,SOTA一个接一个,但事件抽取似乎没有多亮眼的设计。
最近笔者重新尝试了事件抽取任务,在之前的关系抽取模型GPLinker的基础上,结合完全子图搜索,设计一个比较简单但相对完备的事件联合抽取模型,依然称之为GPLinker,在此请大家点评一番。
任务简介
事件抽取是一个比较综合的任务。一个标准的事件抽取样本如下:
为什么需要残差?一个来自DeepNet的视角
By 苏剑林 | 2022-03-19 | 61827位读者 | 引用在《训练1000层的Transformer究竟有什么困难?》中我们介绍了微软提出的能训练1000层Transformer的DeepNet技术。而对于DeepNet,读者一般也有两种反应,一是为此感到惊叹而点赞,另一则是觉得新瓶装旧酒没意思。出现后一种反应的读者,往往是因为DeepNet所提出的两个改进点——增大恒等路径权重和降低残差分支初始化——实在过于稀松平常,并且其他工作也出现过类似的结论,因此很难有什么新鲜感。
诚然,单从结论来看,DeepNet实在算不上多有意思,但笔者觉得,DeepNet的过程远比结论更为重要,它有意思的地方在于提供了一个简明有效的梯度量级分析思路,并可以用于分析很多相关问题,比如本文要讨论的“为什么需要残差”,它就可以给出一个比较贴近本质的答案。
增量爆炸
为什么需要残差?答案是有了残差才更好训练深层模型,这里的深层可能是百层、千层甚至万层。那么问题就变成了为什么没有残差就不容易训练深层模型呢?








最近评论