9
Aug
seq2seq之双向解码
By 苏剑林 | 2019-08-09 | 47085位读者 | 引用在文章《玩转Keras之seq2seq自动生成标题》中我们已经基本探讨过seq2seq，并且给出了参考的Keras实现。
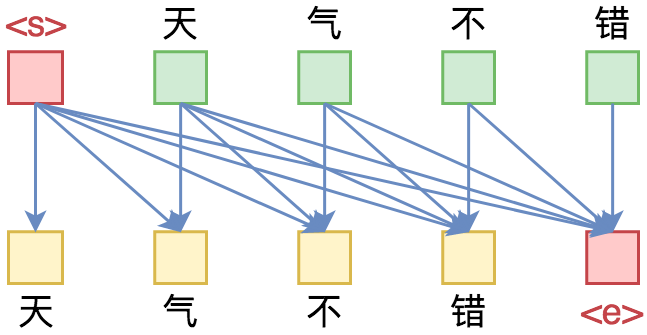
本文则将这个seq2seq再往前推一步，引入双向的解码机制，它在一定程度上能提高生成文本的质量（尤其是生成较长文本时）。本文所介绍的双向解码机制参考自《Synchronous Bidirectional Neural Machine Translation》，最后笔者也是用Keras实现的。
背景介绍
研究过seq2seq的读者都知道，常见的seq2seq的解码过程是从左往右逐字（词）生成的，即根据encoder的结果先生成第一个字；然后根据encoder的结果以及已经生成的第一个字，来去生成第二个字；再根据encoder的结果和前两个字，来生成第三个词；依此类推。总的来说，就是在建模如下概率分解
\begin{equation}p(Y|X)=p(y_1|X)p(y_2|X,y_1)p(y_3|X,y_1,y_2)\cdots\label{eq:p}\end{equation}
20
Aug
开源一版DGCNN阅读理解问答模型（Keras版）
By 苏剑林 | 2019-08-20 | 74709位读者 | 引用去年写过《基于CNN的阅读理解式问答模型：DGCNN》，介绍了一个纯卷积的简单的问答模型。当时是用Tensorflow实现的，而且没有开源，这几天抽空用Keras复现了一下，决定开源。
模型综述
关于DGCNN的基本介绍，这里不再赘述。本文的模型并不是之前模型的重复实现，而是有所改动，这里只介绍一下被改动的地方。
1、这里放出的模型，线下验证集的分数大概是0.72（之前大约是0.75）；
2、本次模型以字为单位，使用笔者之前探索出来的“字词混合Embedding”（之前是以词为单位）；
3、本次模型完全去掉了人工特征（之前用了8个人工特征）；
4、本次模型去掉了位置Embedding（之前将位置Embedding拼接到输入上）；
5、模型架构和训练细节有所微调。
9
Sep
重新写了之前的新词发现算法：更快更好的新词发现
By 苏剑林 | 2019-09-09 | 98057位读者 | 引用新词发现是NLP的基础任务之一，主要是希望通过无监督发掘一些语言特征（主要是统计特征），来判断一批语料中哪些字符片段可能是一个新词。本站也多次围绕“新词发现”这个话题写过文章，比如：
在这些文章之中，笔者觉得理论最漂亮的是《基于语言模型的无监督分词》，而作为新词发现算法来说综合性能比较好的应该是《更好的新词发现算法》，本文就是复现这篇文章的新词发现算法。
13
Nov
n维空间下两个随机向量的夹角分布
By 苏剑林 | 2019-11-13 | 140971位读者 | 引用昨天群里大家讨论到了$n$维向量的一些反直觉现象，其中一个话题是“一般$n$维空间下两个随机向量几乎都是垂直的”，这就跟二维/三维空间的认知有明显出入了。要从理论上认识这个结论，我们可以考虑两个随机向量的夹角$\theta$分布，并算算它的均值方差。
概率密度
首先，我们来推导$\theta$的概率密度函数。呃，其实也不用怎么推导，它是$n$维超球坐标的一个直接结论。
要求两个随机向量之间的夹角分布，很显然，由于各向同性，所以我们只需要考虑单位向量，而同样是因为各向同性，我们只需要固定其中一个向量，考虑另一个向量随机变化。不是一般性，考虑随机向量为
\begin{equation}\boldsymbol{x}=(x_1,x_2,\dots,x_n)\end{equation}
而固定向量为
\begin{equation}\boldsymbol{y}=(1,0,\dots,0)\end{equation}
18
Sep
从语言模型到Seq2Seq：Transformer如戏，全靠Mask
By 苏剑林 | 2019-09-18 | 335289位读者 | 引用相信近一年来（尤其是近半年来），大家都能很频繁地看到各种Transformer相关工作（比如Bert、GPT、XLNet等等）的报导，连同各种基础评测任务的评测指标不断被刷新。同时，也有很多相关的博客、专栏等对这些模型做科普和解读。
单向语言模型图示。每预测一个token，只依赖于前面的token。
俗话说，“外行看热闹，内行看门道”，我们不仅要在“是什么”这个层面去理解这些工作，我们还需要思考“为什么”。这个“为什么”不仅仅是“为什么要这样做”，还包括“为什么可以这样做”。比如，在谈到XLNet的乱序语言模型时，我们或许已经从诸多介绍中明白了乱序语言模型的好处，那不妨更进一步思考一下：
为什么Transformer可以实现乱序语言模型？是怎么实现的？RNN可以实现吗？
本文从对Attention矩阵进行Mask的角度，来分析为什么众多Transformer模型可以玩得如此“出彩”的基本原因，正如标题所述“Transformer如戏，全靠Mask”，这是各种花式Transformer模型的重要“门道”之一。
读完本文，你或许可以了解到：
1、Attention矩阵的Mask方式与各种预训练方案的关系；
2、直接利用预训练的Bert模型来做Seq2Seq任务。
16
Jan
从几何视角来理解模型参数的初始化策略
By 苏剑林 | 2020-01-16 | 97695位读者 | 引用对于复杂模型来说，参数的初始化显得尤为重要。糟糕的初始化，很多时候已经不单是模型效果变差的问题了，还更有可能是模型根本训练不动或者不收敛。在深度学习中常见的自适应初始化策略是Xavier初始化，它是从正态分布$\mathcal{N}\left(0,\frac{2}{fan_{in} + fan_{out}}\right)$中随机采样而构成的初始权重，其中$fan_{in}$是输入的维度而$fan_{out}$是输出的维度。其他初始化策略基本上也类似，只不过假设有所不同，导致最终形式略有差别。
标准的初始化策略的推导是基于概率统计的，大概的思路是假设输入数据的均值为0、方差为1，然后期望输出数据也保持均值为0、方差为1，然后推导出初始变换应该满足的均值和方差条件。这个过程理论上没啥问题，但在笔者看来依然不够直观，而且推导过程的假设有点多。本文则希望能从几何视角来理解模型的初始化方法，给出一个更直观的推导过程。
信手拈来的正交
前者时间笔者写了《n维空间下两个随机向量的夹角分布》，其中的一个推论是
推论1： 高维空间中的任意两个随机向量几乎都是垂直的。
24
Feb
CRF用过了，不妨再了解下更快的MEMM？
By 苏剑林 | 2020-02-24 | 49420位读者 | 引用HMM、MEMM、CRF被称为是三大经典概率图模型，在深度学习之前的机器学习时代，它们被广泛用于各种序列标注相关的任务中。一个有趣的现象是，到了深度学习时代，HMM和MEMM似乎都“没落”了，舞台上就只留下CRF。相信做NLP的读者朋友们就算没亲自做过也会听说过BiLSTM+CRF做中文分词、命名实体识别等任务，却几乎没有听说过BiLSTM+HMM、BiLSTM+MEMM的，这是为什么呢？
今天就让我们来学习一番MEMM，并且通过与CRF的对比，来让我们更深刻地理解概率图模型的思想与设计。
模型推导
MEMM全称Maximum Entropy Markov Model，中文名可译为“最大熵马尔可夫模型”。不得不说，这个名字可能会吓退80%的初学者：最大熵还没搞懂，马尔可夫也不认识，这两个合起来怕不是天书？而事实上，不管是MEMM还是CRF，它们的模型都远比它们的名字来得简单，它们的概念和设计都非常朴素自然，并不难理解。
最近评论