11
Aug
谈谈“民科”——兼谈如何推翻爱恩斯坦?
By 苏剑林 | 2010-08-11 | 159345位读者 | 引用民科,是“平民科学家”的简称,本来,无论怎么看,这个词都是一个褒义词,代表了一群默默进行科学研究的人,本来,我等天文爱好者都可以用上“民科”这一漂亮词语。然而,“得益于”某些民科(至少在中国是这样的)的狂妄自大,使得“民科”成为了另外一群人的代名词。他们他们从最基础的物理学比如牛顿力学开始,就和正统的物理学分道扬镳。他们使用的专业术语跟正统的物理学都不同。你说东,他说西,以致于民科和专业人士完全不能交流。还有一些民科从易经八卦这些所谓的哲学原理出发,提出一些自以为是的邪乎学说,完全不在物理学的轨道上。这一群人,仿佛自认为自己是救世主,他们就是崭新而又来源已久的新“民科”。由此看,民科和物理学之间存在一个无法沟通的真空。
23
Aug
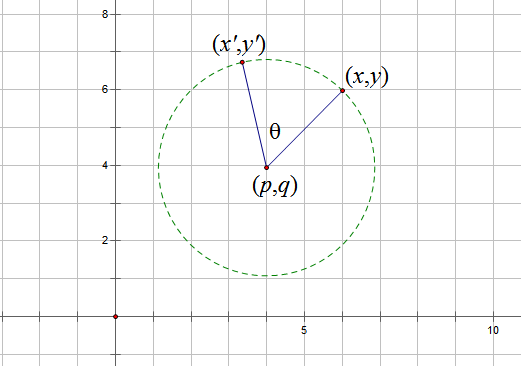
《向量》系列——4.天旋地转(向量,复数,极坐标)
By 苏剑林 | 2010-08-23 | 42467位读者 | 引用
26
Aug
“用户评价”靠谱吗?
By 苏剑林 | 2010-08-26 | 22927位读者 | 引用
3
Oct
《向量》系列——5.平面向量微分方程与复数
By 苏剑林 | 2010-10-03 | 21775位读者 | 引用
6
Oct
《积分公式大全》网络版本
By 苏剑林 | 2010-10-06 | 22196位读者 | 引用为了方便各位读者查阅,BoJone特意制作了这个积分公式表的电子版本。
数学公式采用JsMath技术显示,为了能够更清晰地显示数学公式,推荐读者下载TeX-fonts字体。
原著的具体说明和下载,请点击










最近评论