科学空间|Scientific Spaces

事实上，O-GAN的发现，已经达到了我对GAN的理想追求，使得我可以很惬意地跳出GAN的大坑了。所以现在我会试图探索更多更广的研究方向，比如NLP中还没做过的任务，又比如图神经网络，又或者其他有趣的东西。

不过，在此之前，我想把之前的GAN的学习结果都记录下来。

这篇文章中，我们来梳理一下GAN的架构发展情况，当然主要的是生成器的发展，判别器一直以来的变动都不大。还有，本文介绍的是GAN在图像方面的模型架构发展，跟NLP的SeqGAN没什么关系。

此外，关于GAN的基本科普，本文就不再赘述了。

棋盘效应图示，体现为放大之后出现如国际象棋棋盘一样的交错效应。图片来自文章《Deconvolution and Checkerboard Artifacts》

点击阅读全文...

前些天刷Arxiv看到新文章《Self-Orthogonality Module: A Network Architecture Plug-in for Learning Orthogonal Filters》（下面简称“原论文”），看上去似乎有点意思，于是阅读了一番，读完确实有些收获，在此记录分享一下。

给全连接或者卷积模型的核加上带有正交化倾向的正则项，是不少模型的需求，比如大名鼎鼎的BigGAN就加入了类似的正则项。而这篇论文则引入了一个新的正则项，笔者认为整个分析过程颇为有趣，可以一读。

为什么希望正交？

在开始之前，我们先约定：本文所出现的所有一维向量都代表列向量。那么，现在假设有一个$d$维的输入样本$\boldsymbol{x}\in \mathbb{R}^d$，经过全连接或卷积层时，其核心运算就是：
\begin{equation}\boldsymbol{y}^{\top}=\boldsymbol{x}^{\top}\boldsymbol{W},\quad \boldsymbol{W}\triangleq (\boldsymbol{w}_1,\boldsymbol{w}_2,\dots,\boldsymbol{w}_k)\label{eq:k}\end{equation}
其中$\boldsymbol{W}\in \mathbb{R}^{d\times k}$是一个矩阵，它就被称“核”（全连接核／卷积核），而$\boldsymbol{w}_1,\boldsymbol{w}_2,\dots,\boldsymbol{w}_k\in \mathbb{R}^{d}$是该矩阵的各个列向量。

点击阅读全文...

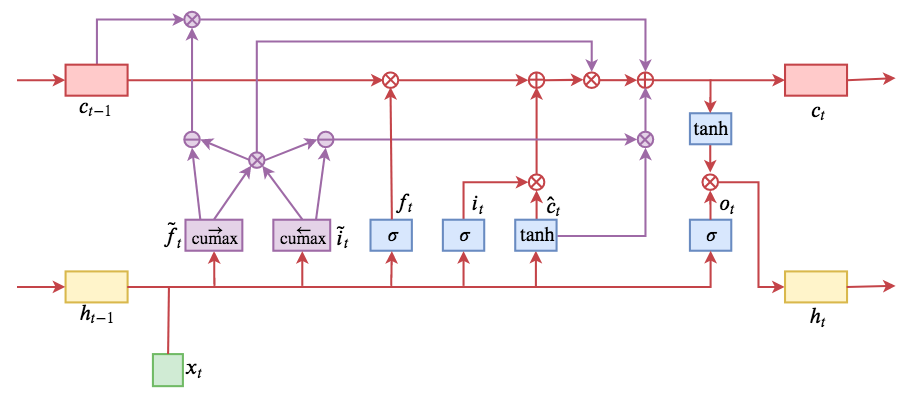
今天介绍一个有意思的LSTM变种：ON-LSTM，其中“ON”的全称是“Ordered Neurons”，即有序神经元，换句话说这种LSTM内部的神经元是经过特定排序的，从而能够表达更丰富的信息。ON-LSTM来自文章《Ordered Neurons: Integrating Tree Structures into Recurrent Neural Networks》，顾名思义，将神经元经过特定排序是为了将层级结构（树结构）整合到LSTM中去，从而允许LSTM能自动学习到层级结构信息。这篇论文还有另一个身份：ICLR 2019的两篇最佳论文之一，这表明在神经网络中融合层级结构（而不是纯粹简单地全向链接）是很多学者共同感兴趣的课题。

ON-LSTM运算流程示意图。主要是将分段函数用cumax光滑化变成可导。

笔者留意到ON-LSTM是因为机器之心的介绍，里边提到它除了提高了语言模型的效果之外，甚至还可以无监督地学习到句子的句法结构！正是这一点特性深深吸引了我，而它最近获得ICLR 2019最佳论文的认可，更是坚定了我要弄懂它的决心。认真研读、推导了差不多一星期之后，终于有点眉目了，遂写下此文。

在正式介绍ON-LSTM之后，我忍不住要先吐槽一下这篇文章实在是写得太差了，将一个明明很生动形象的设计，讲得异常晦涩难懂，其中的核心是$\tilde{f}_t$和$\tilde{i}_t$的定义，文中几乎没有任何铺垫就贴了出来，也没有多少诠释，开始的读了好几次仍然像天书一样...总之，文章写法实在不敢恭维～

点击阅读全文...

印象中很早之前就看到过VQ-VAE，当时对它并没有什么兴趣，而最近有两件事情重新引起了我对它的兴趣。一是VQ-VAE-2实现了能够匹配BigGAN的生成效果（来自机器之心的报道）；二是我最近看一篇NLP论文《Unsupervised Paraphrasing without Translation》时发现里边也用到了VQ-VAE。这两件事情表明VQ-VAE应该是一个颇为通用和有意思的模型，所以我决定好好读读它。

个人复现的VQ-VAE在CelebA上的重构效果。可以留意到细节保留得还不错，但稍微放大后能留意到仍有一些模糊感。

点击阅读全文...

最近了解到一种称为“BERT-of-Theseus”的BERT模型压缩方法，来自论文《BERT-of-Theseus: Compressing BERT by Progressive Module Replacing》。这是一种以“可替换性”为出发点所构建的模型压缩方案，相比常规的剪枝、蒸馏等手段，它整个流程显得更为优雅、简洁。本文将对该方法做一个简要的介绍，给出一个基于bert4keras的实现，并验证它的有效性。

BERT-of-Theseus，原作配图

模型压缩

首先，我们简要介绍一下模型压缩。不过由于笔者并非专门做模型压缩的，也没有经过特别系统的调研，所以该介绍可能显得不专业，请读者理解。

点击阅读全文...

“法研杯”算是近年来比较知名的NLP赛事之一，今年是第三届，包含四个赛道，其中有一个“司法摘要”赛道引起了我们的兴趣。经过了解，这是面向法律领域裁判文书的长文本摘要生成，这应该是国内第一个公开的长文本生成任务和数据集。过去一年多以来，我们在文本生成方面都有持续的投入和探索，所以决定选择该赛道作为检验我们研究成果的“试金石”。很幸运，我们最终以微弱的优势获得了该赛道的第一名。在此，我们对我们的比赛模型做一个总结和分享。

比赛榜单截图

在该比赛中，我们跳出了纯粹炼丹的过程，通过新型的Copy机制、Sparse Softmax等颇具通用性的新方法提升了模型的性能。整体而言，我们的模型比较简洁有效，而且可以做到端到端运行。窃以为我们的结果对工程和研究都有一定的参考价值。

点击阅读全文...

BERT-flow来自论文《On the Sentence Embeddings from Pre-trained Language Models》，中了EMNLP 2020，主要是用flow模型校正了BERT出来的句向量的分布，从而使得计算出来的cos相似度更为合理一些。由于笔者定时刷Arixv的习惯，早在它放到Arxiv时笔者就看到了它，但并没有什么兴趣，想不到前段时间小火了一把，短时间内公众号、知乎等地出现了不少的解读，相信读者们多多少少都被它刷屏了一下。

从实验结果来看，BERT-flow确实是达到了一个新SOTA，但对于这一结果，笔者的第一感觉是：不大对劲！当然，不是说结果有问题，而是根据笔者的理解，flow模型不大可能发挥关键作用。带着这个直觉，笔者做了一些分析，果不其然，笔者发现尽管BERT-flow的思路没有问题，但只要一个线性变换就可以达到相近的效果，flow模型并不是十分关键。

余弦相似度的假设

一般来说，我们语义相似度比较或检索，都是给每个句子算出一个句向量来，然后算它们的夹角余弦来比较或者排序。那么，我们有没有思考过这样的一个问题：余弦相似度对所输入的向量提出了什么假设呢？或者说，满足什么条件的向量用余弦相似度做比较效果会更好呢？

点击阅读全文...

上一篇文章中，我们比较详细地介绍了Johnson-Lindenstrauss引理（JL引理）的理论推导，这一篇我们来关注它的应用。

作为一个内容上本身就跟降维相关的结论，JL引理最基本的自然就是作为一个降维方法来用。但除了这个直接应用外，很多看似不相关的算法，比如局部敏感哈希（LSH）、随机SVD等，本质上也依赖于JL引理。此外，对于机器学习模型来说，JL引理通常还能为我们的维度选择提供一些理论解释。

降维的工具

JL引理提供了一个非常简单直接的“随机投影”降维思路：

给定$N$个向量$v_1,v_2,\cdots,v_N\in\mathbb{R}^m$，如果想要将它降到$n$维，那么只需要从$\mathcal{N}(0,1/n)$中采样一个$n\times m$矩阵$A$，然后$Av_1,Av_2,\cdots,Av_N$就是降维后的结果。

点击阅读全文...