有限素域上的乘法群是循环群
By 苏剑林 | 2015-01-20 | 85161位读者 | 引用对于任意的素数$p$,集合$\mathbb{Z}_p=\{0,1,2,\dots,p-1\}$在模$p$的加法和乘法之下,构成一个域,这是学过抽象代数或者初等数论的读者都会知道的一个事实。其中,根据域的定义,$\mathbb{Z}_p$首先要在模$p$的加法下成为一个交换群,而且由于$\mathbb{Z}_p$的特殊性,它还是一个循环群,这也是比较平凡的事实。但是,考虑乘法呢?
首先,$0$是没有逆元的,我们考虑乘法,是在$\mathbb{Z}^\cdot _p=\mathbb{Z}_p \verb|\| \{0\}=\{1,2,\dots,p-1\}$上考虑的。如果我说,$\mathbb{Z}^\cdot _p$在模$p$之下的乘法也作成一个循环群,这结论就不是很平凡的了!然而这确实是事实,对于所有的素数$p$均成立。而有了这事实,数论中的一些结论就会相当显然了,比如当$d\mid (p-1)$时,$\mathbb{Z}_p$中的$d$次剩余就只有$\frac{p-1}{d}$个了,这是循环群的基本结论。
在《数学天书中的证明》一书中,有该结论的一个证明,但这个证明是存在性的,而我在另外一本书上也看到过类似的存在性证明,也就是说,似乎流行的证明都是存在性的,它告诉我们$\mathbb{Z}^\cdot _p$是一个循环群,但是没告诉我们怎么找到它的生成元。而事实上,高斯在他的《算术探索》中就给出了一个构造性的证明。(在数论中,本文的结论是“原根”那一章的基本知识。)下面笔者正是要重复高斯的证明,供读者参考。
从Knotsevich在黑板上写的级数题目谈起
By 苏剑林 | 2015-02-27 | 31233位读者 | 引用柯西命题:盯着它到显然成立为止!
By 苏剑林 | 2015-04-19 | 45594位读者 | 引用数学分析中数列极限部分,有一个很基本的“柯西命题”:
如果$\lim_{n\to\infty} x_n=a$,则
$$\lim_{n\to\infty}\frac{x_1+x_2+\dots+x_n}{n}=a$$
本文所要谈的便是这个命题,当然还包括类似的一些题目。
柯西命题的证明
柯西命题的证明并不难,只需要根据极限收敛的定义,由于$\lim_{n\to\infty} x_n=a$,所以任意给定$\varepsilon > 0$,存在足够大的$N$,使得对于任意的$n > N$,都有
$$\left|x_n - a\right| < \varepsilon/2\quad(\forall n > N)$$
闲聊:神经网络与深度学习
By 苏剑林 | 2015-06-06 | 73927位读者 | 引用在所有机器学习模型之中,也许最有趣、最深刻的便是神经网络模型了。笔者也想献丑一番,说一次神经网络。当然,本文并不打算从头开始介绍神经网络,只是谈谈我对神经网络的个人理解。如果希望进一步了解神经网络与深度学习的朋友,请移步阅读下面的教程:
http://deeplearning.stanford.edu/wiki/index.php/UFLDL教程
http://blog.csdn.net/zouxy09/article/details/8775360
机器分类
这里以分类工作为例,数据挖掘或机器学习中,有很多分类的问题,比如讲一句话的情况进行分类,粗略点可以分类为“积极”或“消极”,精细点分为开心、生气、忧伤等;另外一个典型的分类问题是手写数字识别,也就是将图片分为10类(0,1,2,3,4,5,6,7,8,9)。因此,也产生了很多分类的模型。
exp(1/2 t^2+xt)级数展开的图解技术
By 苏剑林 | 2015-08-13 | 32500位读者 | 引用本文要研究的是关于$t$的函数
$$\exp\left(\frac{1}{2}t^2+xt\right)$$
在$t=0$处的泰勒展开式。显然,它并不困难,手算或者软件都可以做出来,答案是:
$$1+x t+\frac{1}{2} \left(x^2+1\right) t^2+\frac{1}{6}\left(x^3+3 x\right) t^3 +\frac{1}{24} \left(x^4+6 x^2+3\right) t^4 + \dots$$
不过,本文将会给出笔者构造的该级数的一个图解方法。通过这个图解方法比较比较直观而方便地手算出展开式的前面一些项。后面我们再来谈谈这种图解技术的起源以及进一步的应用。
级数的图解方法:说明
首先,很明显要写出这个级数,关键是写出展开式的每一项,也就是要求出
$$f_k (x) = \left.\frac{d^k}{dt^k}\exp\left(\frac{1}{2}t^2+xt\right)\right|_{t=0}$$
$f_k (x)$是一个关于$x$的$k$次整系数多项式,$k$是展开式的阶,也是求导的阶数。
这里,我们用一个“点”表示一个$x$,用“两点之间的一条直线”表示“相乘”,那么,$x^2$就可以表示成
2015诺贝尔医学奖:中国人在内
By 苏剑林 | 2015-10-05 | 24980位读者 | 引用“熵”不起:从熵、最大熵原理到最大熵模型(二)
By 苏剑林 | 2015-12-11 | 88710位读者 | 引用上集回顾
在第一篇中,笔者介绍了“熵”这个概念,以及它的一些来龙去脉。熵的公式为
$$S=-\sum_x p(x)\log p(x)\tag{1}$$
或
$$S=-\int p(x)\log p(x) dx\tag{2}$$
并且在第一篇中,我们知道熵既代表了不确定性,又代表了信息量,事实上它们是同一个概念。
说完了熵这个概念,接下来要说的是“最大熵原理”。最大熵原理告诉我们,当我们想要得到一个随机事件的概率分布时,如果没有足够的信息能够完全确定这个概率分布(可能是不能确定什么分布,也可能是知道分布的类型,但是还有若干个参数没确定),那么最为“保险”的方案是选择使得熵最大的分布。
最大熵原理
承认我们的无知
很多文章在介绍最大熵原理的时候,会引用一句著名的句子——“不要把鸡蛋放在同一个篮子里”——来通俗地解释这个原理。然而,笔者窃以为这句话并没有抓住要点,并不能很好地体现最大熵原理的要义。笔者认为,对最大熵原理更恰当的解释是:承认我们的无知!
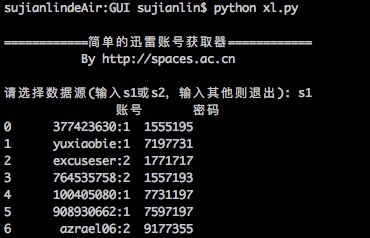
简单的迅雷VIP账号获取器(Python)
By 苏剑林 | 2016-01-20 | 33607位读者 | 引用在Windows工作的时候,经常会用迅雷下载东西,如果速度慢或者没资源,尤其是一些比较冷门的视频,迅雷的VIP会员服务总能够帮上大忙。后来无意间发现了有个“迅雷VIP账号获取器”的软件,可以获取一些临时的VIP账号供使用,这可是个好东西,因为开通迅雷会员虽然不贵,但是我又不经常下载,所以老感觉有点浪费,而有了这个之后,我随时下点东西都可以免费用了。
最近转移到了Mac上,而Mac也有迅雷,但那个账号获取器是exe的,不能在Mac运行。本以为获取器的构造会很复杂,谁知道,经过抓包研究,发现那个账号获取器的原理极其简单,说白了,就是一个简单的爬虫,以下这两个网站提供账号,它就到相应的抓取账号而已:
http://yunbo.xinjipin.com/
http://www.fenxs.com
据此,我也用Python简单写了一个,主要是方便我在Mac使用。读者如果有需要,也可以下载使用,代码兼容2.x和3.x的版本。主要的库是requests和re,pandas和sys的使用只不过是为了更加人性化。本来想用Tkinter写一个简单的GUI的,但是想想看,还是没必要了~~











最近评论