用PyPy提高Python脚本执行效率
By 苏剑林 | 2014-06-11 | 24135位读者 | 引用在《两百万前素数之和与前两百万素数之和》中,我们用Python求了前两百万的素数和以及两百万前的素数和,并且得到了在Python 3.3中的执行时间如下:
两百万前的素数之和:
142913828922
time: 2.4048174478605646前两百万的素数之和:
31381137530481
time: 46.75734807838953
于是想办法提高python脚本的执行效率,我觉得在算法方面,优化空间已经比较小了,于是考虑执行器上的优化。在搜索的无意间我看到了一个名词——Psyco!这是python的一个外部模块,导入后可以加快.py脚本的执行。网上也有《用 Psyco 让 Python 运行得像 C一样快》、《利用 psyco 让 Python 程序执行更快》之类的文章,说明Psyco确实是一个可行的选择,于是就跃跃欲试了,后来了解到Psyco在2012年已经停止开发,只支持到Python 2.4版本,目前它由 PyPy所接替。于是我就下载了PyPy。
如何看费曼的讲义和朗道的教程?
By 苏剑林 | 2014-03-25 | 67783位读者 | 引用事实上,取这个标题,有点狂妄自大、班门弄斧的感觉。原因之一是我自己并非物理专业学生,也没有学好物理。再者,我自己也没有读过多少费曼和朗道的书,谈不上“饱读”费曼朗道,又何以指导大家呢?本文很荣幸得到了高教社的王超编辑(新浪微博 @朗道集结号 )在微信上的推荐,在此表示十分的感谢。
朗道集结号
朗道、费曼、薛定谔、泡利、狄拉克、温伯格……大师在这里等着你,微信号:ldjjhwx
但是,结合自己在阅读他们的著作的感受,以及自己学习科学的过程,谈谈我对他们的著作的看法。
什么才是最简洁的方式?
相信不少读者觉得朗道的教程比费曼的讲义要深,感觉朗道的书总有大量的数学公式,而费曼的书则轻松一些。笔者开始也有这样的感觉,但是慢慢读下去,才感到费曼的书甚至比朗道的困难。
在进入讨论之前,我们不妨先想一下:什么才是理解物理的最简洁方式?数学越复杂,就越不好吗?
一本对称闯物理:相对论力学(二)
By 苏剑林 | 2014-03-25 | 18813位读者 | 引用从这个系列的第一篇文章到本文,已经隔了好多天。其实本文的内容是跟第一篇的内容同时完成的,为什么这么久才更新呢?原因有二,其一是随着春天的到来人也开始懒起来了,颓废呀~;其二,我在思考着规范变换的问题。按照朗道《场论》的逻辑,发展完质点力学理论后,下一步就是发展场论,诸如电磁场、引力场等。但是场论中有个让我比较困惑的东西,即场论存在着“规范不变性”。按照一般观点,我们是将规范不变性看作是电磁场方程的一个结果,即推导出电磁场的方程后,“发现”它具有规范不变性。但是如果用本文的方法,即假定场有这种对称性,然后就可以构建出场方程了。可是,为什么场存在着规范不变性,我还未能思考清楚。据我阅读到的资料来看,这个不变性似乎跟广义不变性有关(电磁场也是,这似乎说明即使在平直时空的电磁场理论中也暗示了广义不变性?)。还有,似乎这个不变性需要在量子场论中才能得到比较满意的解释,可是这样的话,就离我还很远了。
好吧,我们还是先回到相对论力学的推导中。
“无”中生有
上一篇文章我们已经构建了相对论力学的无穷小生成元,并进行了延拓。我已经说过,仅需要无穷小的变换形式,就可以构建出完成的相对论力学定律出来(当然这需要一些比较“显然”的假设)。这是个几乎从“无”到有的过程,也是本文标题的含义所在。另一方面,这种从局部到整体的可能性,也给我们带来一些启示:假如方法是普适的,那么可以由此构造出我们需要的物理定律来,包括电磁场、引力场方程等。(当然,我离这个目标还有点远。)
写在前面:作为离散数学的实验作业,我选择了研究数独。经过测试发现,数独的自动推理还不算难,我把两种常规的推理思路转化为了计算机代码,并结合了随机性推导,得到了一个解题能力还不错的数独程序。事实上,本文的程序还可以进一步优化,以得到更高能力的数独程序(只需要整理一下代码,加上几个循环和判断即可),但是我实在太懒,没有动力继续弄下去了,就这样先和大家分享吧。最后,笔者认为本文的算法是更接近我们的思维的算法。
数独简介
历史
相传数独源起于拉丁方阵(Latin Square),1970年代在美国发展,改名为数字拼图(Number Place)、之后流传至日本并发扬光大,以数学智力游戏智力拼图游戏发表。在1984年一本游戏杂志《パズル通信ニコリ》正式把它命名为数独,意思是“在每一格只有一个数字”。后来一位前任香港高等法院的新西兰籍法官高乐德(Wayne Gould)在1997年3月到日本东京旅游时,无意中发现了。他首先在英国的《泰晤士报》上发表,不久其他报纸也发表,很快便风靡全英国,之后他用了6年时间编写了电脑程式,并将它放在网站上,使这个游戏很快在全世界流行。
台湾于2005年5月由“中国时报”首度引进, 且每日连载, 亦造成很大的回响。台湾数独发展协会(Taiwan Sudoku Association, 简称 TSA)亦为世界解谜联盟会员。香港是在2005年7月30日由AM730在创刊时引入数独。中国大陆是在2007年2月28日正式引入数独。北京晚报智力休闲数独俱乐部(数独联盟前身)在新闻大厦举行加入世界谜题联合会的颁证仪式,成为世界谜题联合会的39个成员之一。(引用自“中文维基百科”: http://zh.wikipedia.org/wiki/数独)
两百万前素数之和与前两百万素数之和
By 苏剑林 | 2014-06-10 | 73993位读者 | 引用勾股数的通解及其推广
By 苏剑林 | 2014-07-01 | 22389位读者 | 引用在之前的文章《几何的数与数的几何:超复数的浅探究》中,我们谈及过四元数。四元数源于把复数的$|(a+bi)(c+di)|=|a+bi|\times|c+di|$这一独特的性质进行高维推广。为什么偏爱这一性质?读者或许已经初步知道一些用到复数的这一性质的例子,有几何方面的,也有物理方面的,这一性质为处理模长相关问题带来了美妙的方便。本文介绍它在求三元二次齐次不定方程的整数通解中的应用,这一例子同样展示了复数这一性质的神奇,让我们不得不认同当初哈密顿为了将其推广到高维而不惜耗费十年光阴的努力。
勾股数问题
读者或许已经知道,勾股数,也就是满足
$$x^2+y^2=z^2$$
的所有自然数解,由下面公式给出
$$x=a^2-b^2,\quad y=2ab,\quad z=a^2+b^2$$
[追溯]封装界传奇人物
By 苏剑林 | 2014-07-02 | 20018位读者 | 引用转载理由:现在的deepin和ylmf(已经改为StartOs)都已经在制作自己的Linux,而当初它们都是制作GhostXp的大家。我的初中,即2009年以前,是GhostXP流行的时代,而我当时也加入了这一行列中,发表过一些GhostXP的作品。后来随着时代的发展,XP也就慢慢退出了舞台。我也就随之退出了这个舞台,也因此得以专注科学。但是,几乎所有我的电脑知识,都积累于那个时期,因为为了完成一个系统的制作和推广,需要懂得的电脑技术很多很多,我也得到了充分的锻炼。下面列举的一些人,都是当年GhostXP界的神话人物,有些我并不认识,但其名在当时就如雷贯耳;有些人在当时还十分幸运地加上了他们的QQ。这篇文章实际上已经是很久已经的了,但还是值得回味过去的时间,以此为我的初中时代留下一些回忆。
齐次多项式不等式的机器证明(差分代换)
By 苏剑林 | 2014-07-06 | 42013位读者 | 引用在高中阶段,笔者也像很多学生一样参加过数学竞赛,而在准备数学竞赛的过程中,也做过一些竞赛题,其中当然少不了不等式题目。当时,面对各种各样的不等式证明题,我总是非常茫然,因为看到答案之后,总感觉证明的构造非常神奇,但是每当我自己独立去做时,却总想不出来。于是后来就萌生了“有没有办法可以通用地证明这些不等式?”的想法。为了实现这个目的,当时就想出了本文的技巧——通过牺牲计算的简便性来换取证明的有效性。后来,我虽然没有走上数学竞赛这条路,但这个方法还是保留了下来,近日,在和数学研发论坛的朋友们讨论不等式问题时,重新拾起了这个技巧。
此前,在本博客的文章《对称多项式不等式的“物理证明”》中,已经谈到了这个技巧,只是限制于当时的知识储备,了解并不深入。而在本文中,则进行拓展了。这个技巧在当时是我自己在证明中独立发现的,而现在在网上查找时发现,前辈们(杨路、姚勇、杨学枝等)早已研究过这个技巧,称之为“差分代换”,并且已经探究过它在机器证明中的作用。该技巧可以很一般化地用于齐次/非其次不等式的证明,限于篇幅,本文只谈齐次多项式不等式,特别地,是对称齐次多项式不等式,并且发现某些可以简化之处。







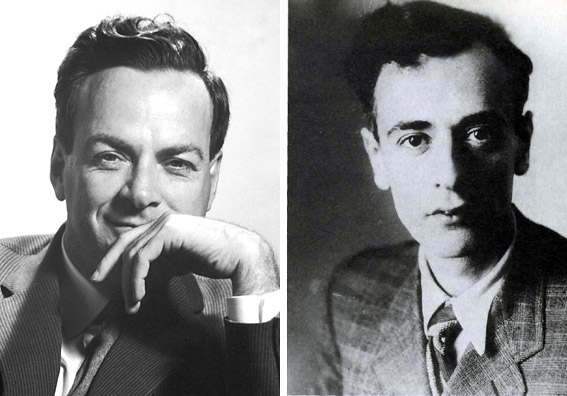

最近评论