从去噪自编码器到生成模型
By 苏剑林 | 2019-10-31 | 154302位读者 |在我看来,几大顶会之中,ICLR的论文通常是最有意思的,因为它们的选题和风格基本上都比较轻松活泼、天马行空,让人有脑洞大开之感。所以,ICLR 2020的投稿论文列表出来之后,我也抽时间粗略过了一下这些论文,确实发现了不少有意思的工作。
其中,我发现了两篇利用去噪自编码器的思想做生成模型的论文,分别是《Learning Generative Models using Denoising Density Estimators》和《Annealed Denoising Score Matching: Learning Energy-Based Models in High-Dimensional Spaces》。由于常规做生成模型的思路我基本都有所了解,所以这种“别具一格”的思路就引起了我的兴趣。细读之下,发现两者的出发点是一致的,但是具体做法又有所不同,最终的落脚点又是一样的,颇有“一题多解”的美妙,遂将这两篇论文放在一起,对比分析一翻。
去噪自编码 #
两篇论文的根本出发点都是去噪自编码器,更准确地说,它利用了去噪自编码器的最优解
基本结果: 若$x,\varepsilon\in \mathbb{R}^d$,并且$x\sim p(x),\varepsilon\sim u(\varepsilon)$,这里$u(\varepsilon)=\mathcal{N}(0,\sigma^2 I_d)$,那么 \begin{equation}\begin{aligned}r(x)=&\,\mathop{\text{argmin}}_{r}\mathbb{E}_{x\sim p(x),\varepsilon\sim \mathcal{N}(0,\sigma^2 I_d)}\left[\Vert r(x + \varepsilon) - x\Vert^2\right] \\ =&\,x + \sigma^2 \nabla_x \,\log\hat{p}(x)\end{aligned}\label{eq:denoise}\end{equation}
其中$\hat{p}(x)=[p*u](x)=\int p(x-\varepsilon)u(\varepsilon) d\varepsilon=\int p(\varepsilon)u(x-\varepsilon) d\varepsilon$指的是分布$p(x)$和$u(\varepsilon)$的卷积运算,具体含义是$x+\varepsilon$的概率密度,换言之,如果$p(x)$代表真实图片的分布,那么如果我们能实现从$\hat{p}(x)$中采样,那么得到的是一批带有高斯噪声的真实图片。
结果$\eqref{eq:denoise}$也就是说加性高斯噪声的最优去噪自编码器是能显式地计算出来,并且结果跟分布的梯度有关。这个结果非常有意思,也非常深刻,值得我们多加回味。比如,式$\eqref{eq:denoise}$告诉我们$r(x)-x$实际上就是对(带噪声的)真实分布梯度的估计,而有了真实分布的梯度,其实可以做很多事情,尤其是生成模型相关的事情。
证明:其实$\eqref{eq:denoise}$的证明并不困难,变分目标得到
\begin{equation}\begin{aligned}&\delta \iint p(x)u(\varepsilon)\left\Vert r(x + \varepsilon) - x\right\Vert_2^2 dx d\varepsilon\\
=&\delta \iint p(x)u(y-x)\left\Vert r(y) - x\right\Vert_2^2 dx dy\\
=&2\iint p(x)u(y-x)\left\langle r(y) - x, \delta r(y)\right\rangle dx dy\\
\end{aligned}\end{equation}
所以$\int p(x)u(y-x)(r(y) - x)dx=0$,即
\begin{equation}r(y) = \frac{\int p(x)u(y-x)x dx}{\int p(x)u(y-x) dx}\end{equation}
代入表达式$u(\varepsilon)=\frac{1}{(2\pi \sigma^2)^{d/2}}\exp\left(-\frac{\left\Vert\varepsilon\right\Vert_2^2}{2\sigma^2}\right)$,即得
\begin{equation}r(y) = y + \sigma^2\nabla_y \log\left[p*u\right](y)\end{equation}
曲径通幽处 #
我们首先来介绍一下《Learning Generative Models using Denoising Density Estimators》的思路。按照GAN和VAE的通常习惯,我们是希望训练一个映射$x=G(z)$,使得从先验分布$q(z)$中采样出来的$z$都能被映射为一个真实样本,用概率的话说,那就是希望拉近$p(x)$和下述的$q(x)$的距离:
\begin{equation}q(x) = \int q(z)\delta(x - G_{\theta}(z))dz\end{equation}
为此,GAN常用的优化目标是最小化$KL(q(x)\Vert p(x))$,这个观点可以参考《用变分推断统一理解生成模型(VAE、GAN、AAE、ALI)》和《能量视角下的GAN模型(二):GAN=“分析”+“采样”》。但是,由于前面估计的是$\hat{p}(x)$的梯度,我们可以换个目标:最小化$KL\left(\hat{q}(x)\big\Vert \hat{p}(x)\right)$。
为了,我们可以进行演算:
\begin{equation}\begin{aligned}KL\left(\hat{q}(x)\big\Vert \hat{p}(x)\right)=&\int \hat{q}(x) \log \frac{\hat{q}(x)}{\hat{p}(x)}dx\\
=&\int q(x)u(\varepsilon) \log \frac{\hat{q}(x+\varepsilon)}{\hat{p}(x+\varepsilon)}dx d\varepsilon\\
=&\int q(z)\delta(x-G_{\theta}(z))u(\varepsilon) \log \frac{\hat{q}(x+\varepsilon)}{\hat{p}(x+\varepsilon)}dx d\varepsilon dz\\
=&\int q(z)u(\varepsilon) \log \frac{\hat{q}(G_{\theta}(z)+\varepsilon)}{\hat{p}(G_{\theta}(z)+\varepsilon)}d\varepsilon dz\\
=&\,\mathbb{E}_{z\sim q(z), \varepsilon\sim u(\varepsilon)}\big[\log \hat{q}(G_{\theta}(z)+\varepsilon) - \log \hat{p}(G_{\theta}(z)+\varepsilon)\big]\\
\end{aligned}\label{eq:dae-1}\end{equation}
这个目标需要我们能得到$\log\hat{p}(x)$和$\log\hat{q}(x)$的估计。我们可以用神经网络构建两个$\mathbb{R}^d \to \mathbb{R}$的模型$E_p(x)$和$E_q(x)$,然后分别去最小化
\begin{equation}\begin{aligned}\mathop{\text{argmin}}_{E_p}\mathbb{E}_{x\sim p(x),\varepsilon\sim \mathcal{N}(0,\sigma^2 I_d)}\left[\Vert \nabla_x E_p(x + \varepsilon) + \varepsilon\Vert^2\right]\\
\mathop{\text{argmin}}_{E_q}\mathbb{E}_{x\sim q(x),\varepsilon\sim \mathcal{N}(0,\sigma^2 I_d)}\left[\Vert \nabla_x E_q(x + \varepsilon) + \varepsilon\Vert^2\right]
\end{aligned}\label{eq:e-grad}\end{equation}
也就是用$\nabla_x E_p(x)+x$和$\nabla_x E_q(x)+x$作为去噪自编码器,根据结果$\eqref{eq:denoise}$,我们就有
\begin{equation}\left\{\begin{aligned}\nabla_x E_p(x)+x=x+\sigma^2 \nabla_x \log \hat{p}(x)\\
\nabla_x E_q(x)+x=x+\sigma^2 \nabla_x \log \hat{q}(x)\end{aligned}\right.
\quad\Rightarrow\quad \left\{\begin{aligned}E_p(x) = \sigma^2 \log \hat{p}(x) + C_1\\
E_q(x) = \sigma^2 \log \hat{q}(x) + C_2\end{aligned}\right.\end{equation}
也就是说在相差一个常数的情况下,$E_p(x)$正比于$\log \hat{p}(x)$,$E_q(x)$也正比于$\log \hat{q}(x)$,而常数不影响优化,所以我们可以将$E_p(x)$和$E_q(x)$替换到$\eqref{eq:dae-1}$里边去,得到
\begin{equation}KL\left(\hat{q}(x)\big\Vert \hat{p}(x)\right)\sim\,\mathbb{E}_{z\sim q(z), \varepsilon\sim u(\varepsilon)}\big[E_q(G_{\theta}(z)+\varepsilon) - E_p(G_{\theta}(z)+\varepsilon)\big]\label{eq:dae-2}\end{equation}
这就得到了一个生成模型的流程:
选定先验分布$q(z)$,初始化$G_{\theta}(z)$,事先求好$E_p(x)$。循环执行下面的3步直到收敛:
1、选一批$z\sim q(z)$,选一批噪声$\varepsilon\sim\mathcal{N}(0,\sigma^2 I_d)$,合成一批带噪声的假样本$x = G_{\theta}(z)+\varepsilon$;
2、利用这批带噪声的假样本训练$E_q(x)$;
3、固定$E_p,E_q$,用梯度下降根据$\eqref{eq:dae-2}$更新若干步$G_{\theta}$;
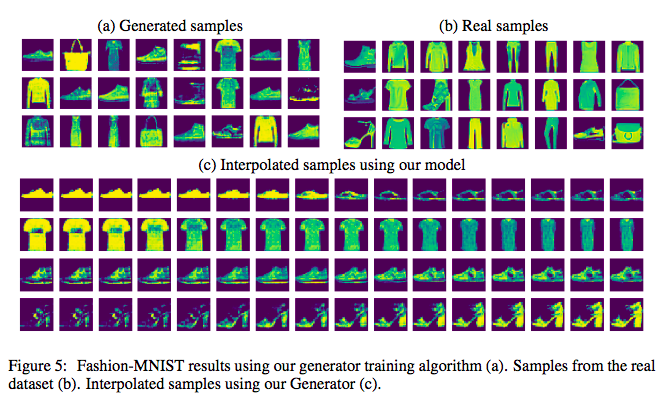
这篇论文的实验比较简单,只做了mnist和fashion mnist的实验,证明了它的可行性:
峰回路转间 #
另外一篇论文《Annealed Denoising Score Matching: Learning Energy-Based Models in High-Dimensional Spaces》就更粗暴直接了,它相当于去噪自编码器跟《能量视角下的GAN模型(三):生成模型=能量模型》的结合。
因为$\eqref{eq:denoise}$已经帮我们得到了$\nabla_x\log\hat{p}(x)=(r(x)-x)/\sigma^2$了(当然这篇论文的实际做法也不是直接用神经网络拟合$r(x)$,而是像$\eqref{eq:e-grad}$一样用神经网络拟合一个标量函数的,但这不影响思想),其实这就能够帮助我们从$\hat{p}(x)$采样了。当然采样出来的图片是有噪声的,我们还需要它采样出来的结果传入$r(x)$去噪一下,即
$$p(x) = \mathbb{E}_{x_{noise}\sim \hat{p}(x)} \big[\delta(x - r(x_{noise}))\big]$$
那具体来说怎么从$\hat{p}(x)$采样呢?Langevin方程!因为已经知道了$\nabla_x\log\hat{p}(x)$,那么下述Langevin方程
\begin{equation}x_{t+1} = x_t + \frac{1}{2}\varepsilon \nabla_x\log\hat{p}(x) + \sqrt{\varepsilon}\alpha,\quad \alpha \sim \mathcal{N}(\alpha;0,1)\label{eq:sde}\end{equation}
当$\varepsilon\to 0$且$t\to\infty$时,序列$\{x_t\}$所服从的分布就是从$\hat{p}(x)$,换句话说,$\hat{p}(x)$是该Langevin方程的静态分布。
于是,从$\hat{p}(x)$采样这个过程,就被《Annealed Denoising Score Matching: Learning Energy-Based Models in High-Dimensional Spaces》用这么一种粗暴直接(但我觉得不优雅)的方法解决了,所以训练完去噪自编码后,就自动地得到了一个生成模型了...
总的过程是:
1、训练去噪自编码器$r(x)$,得到$\nabla_x\hat{p}(x)$;
2、用迭代过程$\eqref{eq:sde}$采样,采样结果是一批带噪声的真实样本;
3、将第2步的采样结果传入$r(x)$去噪,得到无噪声的样本。
当然,论文还有很多细节,论文的核心技巧是用了退火技巧来稳定训练过程,提高生成质量,但笔者对这些并不是很感兴趣,因为我只是想学习一些新奇的生成模型思想,拓宽视野。不过不得不说,虽然做法有点粗暴,这篇论文的生成效果还是有一定的竞争力的,在fashion mnist、CelebA、cifar10都有相当不错的生成效果:
曲终人散时 #
本文介绍了投稿ICLR 2020的两篇类似的论文,都是利用去噪自编码器来做生成模型的,因为之前我没了解过相关思路,所以就饶有兴致对比阅读了一番。
且不说生成效果如何,我觉得它们都是颇具启发性的,能引起我的一些思考(不仅是CV,还包括NLP方面的)。比如Bert的MLM预训练方式本质上也是一个去噪自编码器,那有没有类似$\eqref{eq:denoise}$的结果?或者反过来,类似$\eqref{eq:denoise}$的结果能不能启发我们构造一些新的预训练任务,又或者能不能借此说清楚pretrain + finetune这种流程的本质原理?
转载到请包括本文地址:https://kexue.fm/archives/7038
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Oct. 31, 2019). 《从去噪自编码器到生成模型 》[Blog post]. Retrieved from https://kexue.fm/archives/7038
@online{kexuefm-7038,
title={从去噪自编码器到生成模型},
author={苏剑林},
year={2019},
month={Oct},
url={\url{https://kexue.fm/archives/7038}},
}











July 1st, 2022
这个模型好奇怪啊,看起来同时用了Fisher散度和KL散度的样子
July 1st, 2022
看来MCMC采样过程应该是不如ScoreODE的
额还有点没看懂,这个 $E_p(x)$ 看起来是提前算好的能量函数了咯? 那这样E_p(x) 其实已经包含了很多信息了. 后续又引入 $E_q(x)$ ,总感觉有一点奇怪
$E_p(x)$是训练好的,$E_q(x)$是用来训练生成模型的。因为直接通过$E_p(x)$用Langevin方程采样的话会太慢,所以它想直接训练一个类似GAN的生成过程,这就用到了$E_q(x)$。
恩恩好的,就是这个动机不太清楚.直接用 $E_p(x)$ 约束生成器,应该是会有些问题?
如果直接用 $E_p(x)$ 估计就跟GAN差不太多了?
只用$E_p(x)$是指最大化$E_p(G(z))$吧?要是$G(z)$只生成一张令$E_p(z)$最大的图怎么办?
October 5th, 2023
请问一下(3)是怎么推到(4)的呀?算了很久也没有明白。毕竟不是数学专业出身
反过来推比较容易,直接推是比较难想。
May 16th, 2025
请教苏神,公式2 从第二步到第三步是怎么推导的?
这就跟对$r$求微分一样操作呀。
May 19th, 2025
式$\left(1\right)$就是所谓的Tweedie's Formula吧,感觉和卡尔曼滤波器有点关系。