科学空间|Scientific Spaces

附：期中考过后，课程紧了，自由时间少了，因此科学空间的更新也放缓了。不过BoJone也会尽量地更新一些内容，和大家一同分享学习的乐趣。

闭区间[a,b]上的连续函数?(x)，其最大值为红色点，最小值为蓝色点

上一周和这一周的时间里，BoJone将自己学习物理和极值的一些内容进行了总结和整合，写成了《自然极值》一文。因此从今天起，到十二月的大多数时间里，科学空间将和大家讲述并讨论关于“极值”的问题，希望读者会喜欢这部分内容。当然，我不是专业的研究人员，更不是经验丰富的物理和数学教师，甚至可以说是一个“乳臭未干的小子”，因此，错误在所难免，只希望同好不吝指出，更希冀能够起到我抛出的这一块“砖”能够引出美妙的“玉”。

点击阅读全文...

物理学的美不仅仅表现在简洁的公式上。我们还惊奇地发现，很多物理现象都是按照使某个变量达到极值的方式发生。一个典型的例子就是费马原理，它指出了光的传播路径的一个重要规律：光总是沿着所花时间最短的路径传播。这里我们将简单介绍一下费马原理。

费马原理俗称“最快到达原理”、“最小时间原理”。1657年，费马提出：

从P点到达Q点，在所有可行的路径中，光选择了所需时间最短的一条。

从P点到达Q点，在所有可行的路径中，光选择了所需时间为极值的一条。

这是一个极其奇妙的原理，也是自然界中最神奇的极值之一。作为非生物的光，居然自主地选择了最优路径，成为世界上“效率最高”的东西，这让人不得不佩服宇宙的伟大。这究竟是造物者的精心设计，还是无心之作？

点击阅读全文...

约翰与他同时代的110位学者有通信联系，进行学术讨论的信件约有2500封，其中许多已成为珍贵的科学史文献，例如同他的哥哥雅各布以及莱布尼茨、惠更斯等人关于悬链线、最速降线（即旋轮线）和等周问题的通信讨论，虽然相互争论不断，特别是约翰和雅各布互相指责过于尖刻，使兄弟之间时常造成不快，但争论无疑会促进科学的发展，最速降线问题就导致了变分法的诞生。

有意思的是,1690年约翰·伯努利的哥哥雅可比·伯努利曾提出过悬链线问题向数学界征求答案。即：

固定项链的两端，在重力场中让它自然垂下，求项链的曲线方程.

吊桥上方的悬垂钢索，挂着水珠的蜘蛛网，电杆间的电线都是悬链线。伽利略最早注意到悬链线，猜测悬链线是抛物线。1691年莱布尼兹、惠更斯以及约翰·伯努利各自得到正确答案，所用方法是诞生不久的微积分。

点击阅读全文...

《非线性泛函分析及其应用,第3卷,变分法及最优化》

本篇文章是《自然极值》系列最后一篇文章，估计也是2010年最后一篇文章了。在这个美好的2010年，想必大家一定收获匪浅，BoJone也在2010年成长了很多。在2010年的尾声，BoJone和科学空间都祝大家在新的一年里更加开心快乐，在科学的道路上更快速地前行。

在本文，BoJone将与大家讨论求极值的最基本原理。这一探讨思路受到了天才的费恩曼所著《费恩曼物理讲义》的启迪。我们分别对函数求极值（求导）和泛函数极值（变分）进行一些简略的分析。

一、函数求极值

对于一个函数$y=f(x)$，设想它在$x=x_0$处取到最大值，那么显然对于很小的增量$\Delta x$，有
$$f(x_0+\Delta x) \leq f(x_0)\tag{3}$$根据泰勒级数，我们有
$f(x_0+\Delta x)=f(x_0)+f'(x_0)\Delta x$————(4)

点击阅读全文...

黄果树大瀑布

光学定律无疑是一个美妙的原理，而自然界中还存在另外一个我们随处可见的“公理”。平时的生活中，我们总能看见“水往低处流”的现象，这是因为水处于地球重力场的结果（也正因为如此，某些轻生者的自杀活动才得以顺利进行；当然，我们并不需要为了验证这一点而亲自试验。）。由此我们可以联想到一个名词：重力势能。“水往低处流”意味着什么呢？高度变低了。高度更低意味着什么呢？重力势能降低了！换句话说，自然界中物体有趋于势能最低的倾向。我们可以从这个角度来解释：体系总有趋于稳定的倾向，而拥有的能量（势能）越高，则越不稳定。

点击阅读全文...

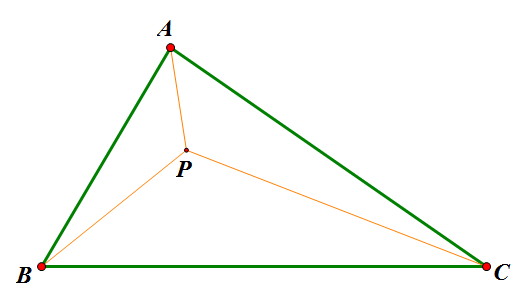
通过上面众多的文字描述，也许你还不大了解这两个原理有何美妙之处，也或者你已经迫不及待地想去应用它们却不知思路。为了不至于让大家产生“审美疲劳”，接下来我们将试图利用这两个原理对费马点问题进行探讨，看看原理究竟是怎么发挥作用的。运用的关键在于：如何通过适当的变换将其与光学或势能联系起来。

费马点问题

传统费马点问题是指在ΔABC中寻找点P，使得$AP+BP+CP$最小的问题；而广义的费马点则改成使$k_1 AP+k_2 BP+k_3 CP$最小。这是很具有现实意义的，是“在三个村庄之间建立一个中转站，如何才能使运送成为最低”之类的最优问题。我们将从光学和势能两个角度对这个问题进行探讨（也许有的读者已经阅读过了利用重力的原理来求解费马点，但是我想光学的方法依然会是你眼前一亮的。）

点击阅读全文...

如果说前面关于这个系列的内容还不能使得读者您感到痛快，那么接下来要讲述的最速降线和悬链线问题也许能够满足你的需要。不过在进入对最速降线问题的理论探讨之前，我们先来讲述一个发生在17世纪的激动人心的数学竞赛的故事。我相信，每一个热爱数学和物理的朋友，都将会为其所振奋，为其所感动。里边渗透的，不仅仅是一次学术的竞争，更是一代又一代的人对真理的追求与探路的不懈精神。

（以下内容来源于网络，科学空间整理）

意大利科学家伽利略在1630年提出一个分析学的基本问题── “一个质点在重力作用下，从一个给定点A到不在它垂直下方的另一点B，如果不计摩擦力，问沿着什么曲线滑下所需时间最短。”这算是这个著名问题的起源了（为什么别人没有想起这个问题呢？所以说大科学家的素质就是思考、创新，要有思想，人没有思想，就和行尸走肉没有什么区别）。可惜的是伽利略说这曲线是圆，但这却是一个错误的答案。

Brachistochrone

点击阅读全文...

通过上一小节的小故事，我们已经能够基本了解最速降线的内容了，它就是要我们求出满足某一极值条件的一个未知函数，由于函数是未知的，因此这类问题被称为“泛分析”。其中还谈到，伯努利利用费马原理巧妙地得出了答案，那么我们现在就再次回顾历史，追寻伯努利的答案，并且寻找进一步的应用。

最速降线-1

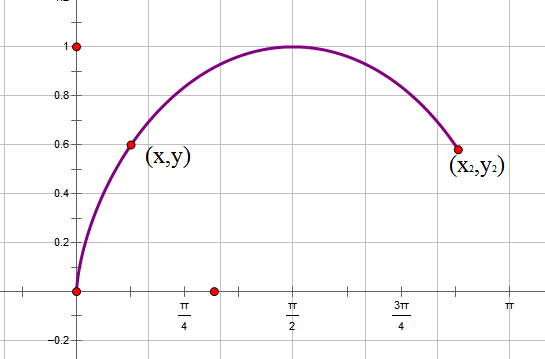
为了计算方便，我们把最速降线倒过来，把初始点设置在原点。在下落过程中，重力势能转化为动能，因此，在点(x,y)处有$\frac{1}{2} mv^2=mgy\Rightarrow v=\sqrt{2gy}$，由于纯粹为了探讨曲线形状，所以我们使g=0.5，即$v=\sqrt{y}$。在点(x,y)处所走的路程为$ds=\sqrt{dy^2+dx^2}=\sqrt{\dot{y}^2+1}dx$，所以时间为$dt=\frac{ds}{v}=\frac{\sqrt{\dot{y}^2+1}dx}{\sqrt{y}}$，于是最速降线问题就是求使$t=\int_0^{x_2} \frac{\sqrt{\dot{y}^2+1}dx}{\sqrt{y}}$最小的函数。

点击阅读全文...