科学空间|Scientific Spaces

随着LLM时代的到来，学术界对于优化器的研究热情似乎有所减退。这主要是因为目前主流的AdamW已经能够满足大多数需求，而如果对优化器“大动干戈”，那么需要巨大的验证成本。因此，当前优化器的变化，多数都只是工业界根据自己的训练经验来对AdamW打的一些小补丁。

不过，最近推特上一个名为“Muon”的优化器颇为热闹，它声称比AdamW更为高效，且并不只是在Adam基础上的“小打小闹”，而是体现了关于向量与矩阵差异的一些值得深思的原理。本文让我们一起赏析一番。

Muon与AdamW效果对比（来源：推特@Yuchenj_UW）

点击阅读全文...

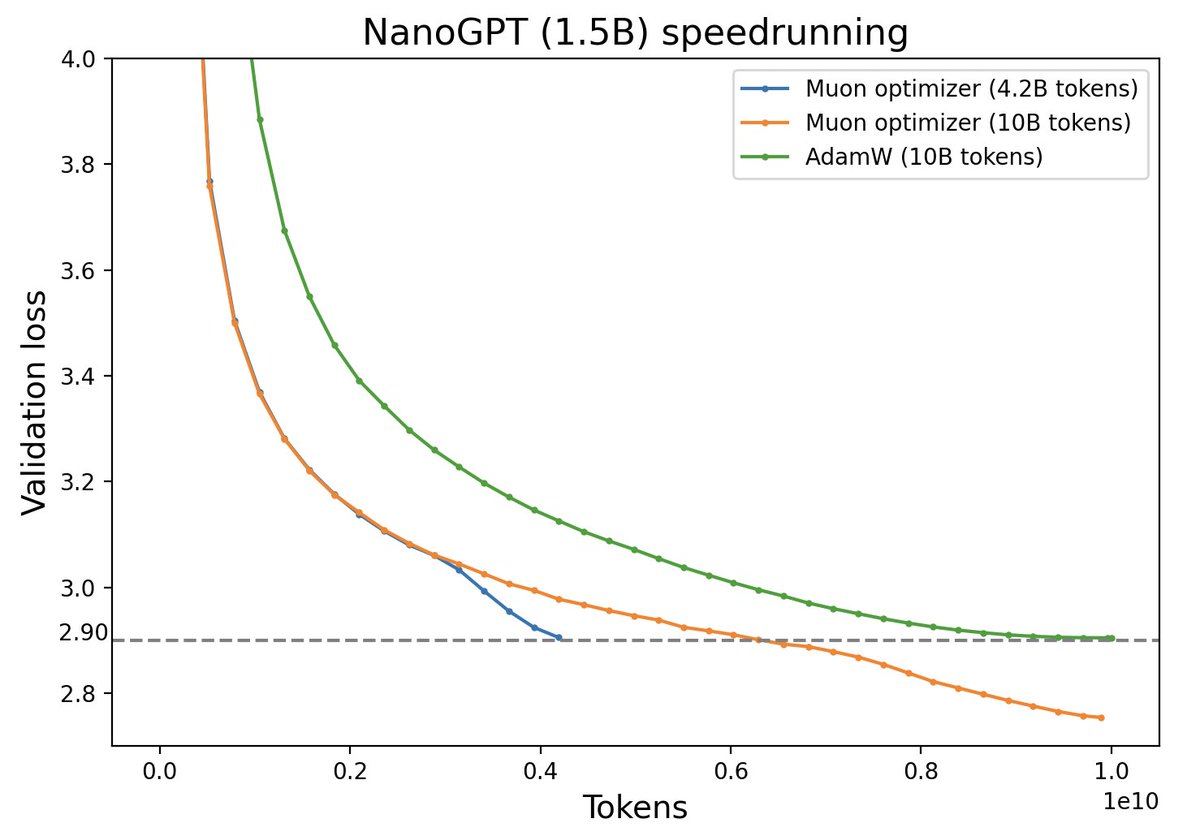
在文章《Muon优化器赏析：从向量到矩阵的本质跨越》中，我们介绍了一个名为“Muon”的新优化器，其中一个理解视角是作为谱范数正则下的最速梯度下降，这似乎揭示了矩阵参数的更本质的优化方向。众所周知，对于矩阵参数我们经常也会加权重衰减（Weight Decay），它可以理解为$F$范数平方的梯度，那么从Muon的视角看，通过谱范数平方的梯度来构建新的权重衰减，会不会能起到更好的效果呢？

那么问题来了，谱范数的梯度或者说导数长啥样呢？用它来设计的新权重衰减又是什么样的？接下来我们围绕这些问题展开。

基础回顾

谱范数（Spectral Norm），又称“$2$范数”，是最常用的矩阵范数之一，相比更简单的$F$范数（Frobenius Norm），它往往能揭示一些与矩阵乘法相关的更本质的信号，这是因为它定义上就跟矩阵乘法相关：对于矩阵参数$\boldsymbol{W}\in\mathbb{R}^{n\times m}$，它的谱范数定义为

点击阅读全文...

再次回到低秩近似之路上。在《低秩近似之路（四）：ID》中，我们介绍了“插值分解（Interpolative Decomposition，ID）”，这是为矩阵$\boldsymbol{M}\in\mathbb{R}^{n\times m}$寻找$\boldsymbol{C}\boldsymbol{Z}$形式的近似的过程，其中$\boldsymbol{C}\in\mathbb{R}^{n\times r}$是矩阵$\boldsymbol{M}$的若干列，而$\boldsymbol{Z}\in\mathbb{R}^{r\times m}$是任意矩阵。

这篇文章我们将介绍CUR分解，它跟插值分解的思想一脉相承，都是以原始矩阵的行、列为“骨架”来构建原始矩阵的近似，跟ID只用行或列之一不同，CUR分解同时用到了行和列。

基本定义

其实这不是本站第一次出现CUR分解了。早在《Nyströmformer：基于矩阵分解的线性化Attention方案》我们就介绍过矩阵的Nyström近似，它实际上就是CUR分解，后来在《利用CUR分解加速交互式相似度模型的检索》还介绍了CUR分解在降低交互式相似度模型的检索复杂度的应用。

点击阅读全文...

笔者前两天在arXiv刷到了一篇新论文《Compressed Image Generation with Denoising Diffusion Codebook Models》，实在为作者的天马行空所叹服，忍不住来跟大家分享一番。

如本文标题所述，作者提出了一个叫DDCM（Denoising Diffusion Codebook Models）的脑洞，它把DDPM的噪声采样限制在一个有限的集合上，然后就可以实现一些很奇妙的效果，比如像VQVAE一样将样本编码为离散的ID序列并重构回来。注意这些操作都是在预训练好的DDPM上进行的，无需额外的训练。

有限集合

由于DDCM只需要用到一个预训练好的DDPM模型来执行采样，所以这里我们就不重复介绍DDPM的模型细节了，对DDPM还不大了解的读者可以回顾我们《生成扩散模型漫谈》系列的（一）、（二）、（三）篇。

点击阅读全文...

前两年福至心灵之下，开了一个“Transformer升级之路”系列，陆续分享了主流Transformer架构的一些改进工作和个人思考，得到了部份读者的认可。这篇文章开始，我们沿着同样的风格，介绍当前另一个主流架构MoE（Mixture of Experts）。

MoE的流行自不必多说，近来火出圈的DeepSeek-V3便是MoE架构，传言GPT-4也是MoE架构，国内最近出的一些模型也有不少用上了MoE。然而，虽然MoE的研究由来已久，但其应用长时间内都不愠不火，大致上是从去年初的《Mixtral of Experts》开始，MoE才逐渐吸引大家的注意力，其显著优点是参数量大，但训练和推理成本都显著低。

但同时MoE也有一些难题，如训练不稳定、负载不均衡、效果不够好等，这也是它早年没有流行起来的主要原因。不过随着这两年关注度的提升，这些问题在很大程度上已经得到解决，我们在接下来的介绍中会逐一谈到这些内容。

点击阅读全文...

在上一篇文章《MoE环游记：1、从几何意义出发》中，我们介绍了MoE的一个几何诠释，旨在通过Dense模型的最佳逼近出发来推导和理解MoE。同时在文末我们也说了，给出MoE的计算公式仅仅是开始，训练一个实际有效的MoE模型还有很多细节补，比如本文要讨论的负载均衡（Load Balance）问题。

负载均衡，即“不患寡而患不均”，说白了就是让每个Expert都在干活，并且都在干尽可能一样多的活，避免某些Expert浪费算力。负载均衡既是充分利用训练算力的需求，也是尽可能发挥MoE大参数量潜力的需求。

需求分析

我们知道，MoE的基本形式是
\begin{equation}\boldsymbol{y} = \sum_{i\in \mathop{\text{argtop}}_k \boldsymbol{\rho}} \rho_i \boldsymbol{e}_i\end{equation}

点击阅读全文...