科学空间|Scientific Spaces

前段时间我们开放了一个名为SimBERT的模型权重，它是以Google开源的BERT模型为基础，基于微软的UniLM思想设计了融检索与生成于一体的任务，来进一步微调后得到的模型，所以它同时具备相似问生成和相似句检索能力。不过当时除了放出一个权重文件和示例脚本之外，未对模型原理和训练过程做进一步说明。在这篇文章里，我们来补充这部分内容。

开源地址：https://github.com/ZhuiyiTechnology/simbert

UniLM

UniLM是一个融合NLU和NLG能力的Transformer模型，由微软在去年5月份提出来的，今年2月份则升级到了v2版本。我们之前的文章《从语言模型到Seq2Seq：Transformer如戏，全靠Mask》就简单介绍过UniLM，并且已经集成到了bert4keras中。

UniLM的核心是通过特殊的Attention Mask来赋予模型具有Seq2Seq的能力。假如输入是“你想吃啥”，目标句子是“白切鸡”，那UNILM将这两个句子拼成一个：[CLS] 你 想 吃 啥 [SEP] 白 切 鸡 [SEP]，然后接如图的Attention Mask：

UniLM的Mask

点击阅读全文...

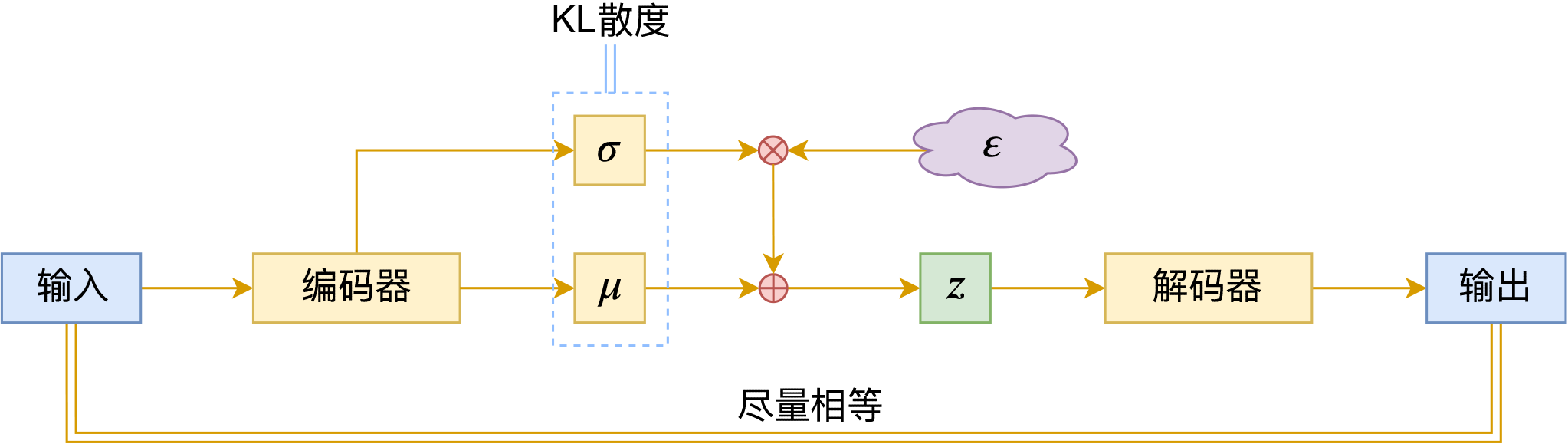
前段时间公司组织技术分享，轮到笔者时，大家希望我讲讲VAE。鉴于之前笔者也写过变分自编码器系列，所以对笔者来说应该也不是特别难的事情，因此就答应了下来，后来仔细一想才觉得犯难：怎么讲才好呢？

变分自编码器示意图

对于VAE来说，之前笔者有两篇比较系统的介绍：《变分自编码器（一）：原来是这么一回事》和《变分自编码器（二）：从贝叶斯观点出发》。后者是纯概率推导，对于不做理论研究的人来说其实没什么意义，也不一定能看得懂；前者虽然显浅一点，但也不妥，因为它是从生成模型的角度来讲的，并没有说清楚“为什么需要VAE”（说白了，VAE可以带来生成模型，但是VAE并不一定就为了生成模型），整体风格也不是特别友好。

笔者想了想，对于大多数不了解但是想用VAE的读者来说，他们应该只希望大概了解VAE的形式，然后想要知道“VAE有什么作用”、“VAE相比AE有什么区别”、“什么场景下需要VAE”等问题的答案，对于这种需求，上面两篇文章都无法很好地满足。于是笔者尝试构思了VAE的一种几何图景，试图从几何角度来描绘VAE的关键特性，在此也跟大家分享一下。

点击阅读全文...

本文介绍来自MIT的一篇ICLR 2020满分论文《Why gradient clipping accelerates training: A theoretical justification for adaptivity》，顾名思义，这篇论文就是分析为什么梯度裁剪能加速深度学习的训练过程。原文很长，公式很多，还有不少研究复杂性的概念，说实话对笔者来说里边的大部分内容也是懵的，不过大概能捕捉到它的核心思想：引入了比常用的L约束更宽松的约束条件，从新的条件出发论证了梯度裁剪的必要性。本文就是来简明分析一下这个过程，供读者参考。

梯度裁剪

假设需要最小化的函数为$f(\theta)$，$\theta$就是优化参数，那么梯度下降的更新公式就是
\begin{equation}\theta \leftarrow \theta-\eta \nabla_{\theta} f(\theta)\end{equation}
其中$\eta$就是学习率。而所谓梯度裁剪（gradient clipping），就是根据梯度的模长来对更新量做一个缩放，比如
\begin{equation}\theta \leftarrow \theta- \eta \nabla_{\theta} f(\theta)\times \min\left\{1, \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert}\right\}\label{eq:clip-1}\end{equation}
或者
\begin{equation}\theta \leftarrow \theta- \eta \nabla_{\theta} f(\theta)\times \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert+\gamma}\label{eq:clip-2}\end{equation}
其中$\gamma > 0$是一个常数。这两种方式都被视为梯度裁剪，总的来说就是控制更新量的模长不超过一个常数，第二种形式也跟RMSProp等自适应学习率优化器相关。此外，更精确地，我们有下面的不等式
\begin{equation}\frac{1}{2}\min\left\{1, \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert}\right\}\leq \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert+\gamma}\leq \min\left\{1, \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert}\right\}\end{equation}
也就是说两者是可以相互控制的，所以其实两者基本是等价的。

点击阅读全文...

前段时间刷Arixv的时候，发现清华大学开源了一个大规模的中文闲聊语料库LCCC（论文链接，项目地址），从开源的文件上来看，这可能是目前开源的数量最大、质量最好的闲聊语料库了，而且还包含了部分多轮对话聊天，总的来说可玩性还是蛮强的。笔者也被它吸引到了，尝试着用它来训练了一个闲聊对话模型，结果看上去还是不错的，在此分享一下自己的经验。

利用单向语言模型做多轮对话示意图

点击阅读全文...

在Seq2Seq的解码过程中，我们是逐个token地递归生成的，直到出现<eos>标记为止，这就是所谓的“自回归”生成模型。然而，研究过Seq2Seq的读者应该都能发现，这种自回归的解码偶尔会出现“根本停不下来”的现象，主要是某个片段反复出现，比如“今天天气不错不错不错不错不错...”、“你觉得我说得对不对不对不对不对不对...”等等，但就是死活不出现<eos>标记。ICML 2020的文章《Consistency of a Recurrent Language Model With Respect to Incomplete Decoding》比较系统地讨论了这个现象，并提出了一些对策，本文来简单介绍一下论文的主要内容。

解码算法

对于自回归模型来说，我们建立的是如下的条件语言模型
\begin{equation}p(y_t|y_{\lt t}, x)\label{eq:p}\end{equation}
那么解码算法就是在已知上述模型时，给定$x$来输出对应的$y=(y_1,y_2,\dots,y_T)$来。解码算法大致可以分为两类：确定性解码算法和随机性解码算法，原论文分别针对这两类解码讨论来讨论了“根本停不下来”问题，所以我们需要来了解一下这两类解码算法。

点击阅读全文...

不少读者都应该知道，损失函数与评测指标的不一致性是机器学习的典型现象之一，比如分类问题中损失函数用交叉熵，评测指标则是准确率或者F1，又比如文本生成中损失函数是teacher-forcing形式的交叉熵，评测指标则是BLEU、ROUGE等。理想情况下，当然是评测什么指标，我们就去优化这个指标，然而评测指标通常都是不可导的，而我们多数都是使用基于梯度的优化器，这就要求最小化的目标必须是可导的，这是不一致性的来源。

前些天在arxiv刷到了一篇名为《MLE-guided parameter search for task loss minimization in neural sequence modeling》的论文，顾名思义，它是研究如何直接优化文本生成的评测指标的。经过阅读，笔者发现这篇论文很有价值，事实上它提供了一种优化评测指标的新思路，适用范围并不局限于文本生成中。不仅如此，它甚至还包含了一种理解可导优化与不可导优化的统一视角。

采样视角

首先，我们可以通过采样的视角来重新看待优化问题：设模型当前参数为$\theta$，优化目标为$l(\theta)$，我们希望决定下一步的更新量$\Delta\theta$，为此，我们先构建分布
\begin{equation}p(\Delta\theta|\theta)=\frac{e^{-[l(\theta + \Delta\theta) - l(\theta)]/\alpha}}{Z(\theta)},\quad Z(\theta) = \int e^{-[l(\theta + \Delta\theta) - l(\theta)]/\alpha} d(\Delta\theta)\end{equation}

点击阅读全文...

本文介绍一种神经网络的可视化方法：积分梯度（Integrated Gradients），它首先在论文《Gradients of Counterfactuals》中提出，后来《Axiomatic Attribution for Deep Networks》再次介绍了它，两篇论文作者都是一样的，内容也大体上相同，后一篇相对来说更易懂一些，如果要读原论文的话，建议大家优先读后一篇。当然，它已经是2016～2017年间的工作了，“新颖”说的是它思路上的创新有趣，而不是指最近发表。

笔者在中文情感分类上对积分梯度的实验效果（越红的token越重要）

所谓可视化，简单来说就是对于给定的输入$x$以及模型$F(x)$，我们想办法指出$x$的哪些分量对模型的决策有重要影响，或者说对$x$各个分量的重要性做个排序，用专业的话术来说那就是“归因”。一个朴素的思路是直接使用梯度$\nabla_x F(x)$来作为$x$各个分量的重要性指标，而积分梯度是对它的改进。然而，笔者认为，很多介绍积分梯度方法的文章（包括原论文），都过于“生硬”（形式化），没有很好地突出积分梯度能比朴素梯度更有效的本质原因。本文试图用自己的思路介绍一下积分梯度方法。

点击阅读全文...

众所周知，尽管基于Attention机制的Transformer类模型有着良好的并行性能，但它的空间和时间复杂度都是$\mathcal{O}(n^2)$级别的，$n$是序列长度，所以当$n$比较大时Transformer模型的计算量难以承受。近来，也有不少工作致力于降低Transformer模型的计算量，比如模型剪枝、量化、蒸馏等精简技术，又或者修改Attention结构，使得其复杂度能降低到$\mathcal{O}(n\log n)$甚至$\mathcal{O}(n)$。

前几天笔者读到了论文《Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention》，了解到了线性化Attention（Linear Attention）这个探索点，继而阅读了一些相关文献，有一些不错的收获，最后将自己对线性化Attention的理解汇总在此文中。

Attention

当前最流行的Attention机制当属Scaled-Dot Attention，形式为
\begin{equation}Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = softmax\left(\boldsymbol{Q}\boldsymbol{K}^{\top}\right)\boldsymbol{V}\label{eq:std-att}\end{equation}
这里的$\boldsymbol{Q}\in\mathbb{R}^{n\times d_k}, \boldsymbol{K}\in\mathbb{R}^{m\times d_k}, \boldsymbol{V}\in\mathbb{R}^{m\times d_v}$，简单起见我们就没显式地写出Attention的缩放因子了。本文我们主要关心Self Attention场景，所以为了介绍上的方便统一设$\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V}\in\mathbb{R}^{n\times d}$，一般场景下都有$n > d$甚至$n\gg d$（BERT base里边$d=64$）。

点击阅读全文...