为什么梯度裁剪能加速训练过程？一个简明的分析

本文介绍来自MIT的一篇ICLR 2020满分论文《Why gradient clipping accelerates training: A theoretical justification for adaptivity》，顾名思义，这篇论文就是分析为什么梯度裁剪能加速深度学习的训练过程。原文很长，公式很多，还有不少研究复杂性的概念，说实话对笔者来说里边的大部分内容也是懵的，不过大概能捕捉到它的核心思想：引入了比常用的L约束更宽松的约束条件，从新的条件出发论证了梯度裁剪的必要性。本文就是来简明分析一下这个过程，供读者参考。

梯度裁剪 #

假设需要最小化的函数为$f(\theta)$，$\theta$就是优化参数，那么梯度下降的更新公式就是
\begin{equation}\theta \leftarrow \theta-\eta \nabla_{\theta} f(\theta)\end{equation}
其中$\eta$就是学习率。而所谓梯度裁剪（gradient clipping），就是根据梯度的模长来对更新量做一个缩放，比如
\begin{equation}\theta \leftarrow \theta- \eta \nabla_{\theta} f(\theta)\times \min\left\{1, \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert}\right\}\label{eq:clip-1}\end{equation}
或者
\begin{equation}\theta \leftarrow \theta- \eta \nabla_{\theta} f(\theta)\times \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert+\gamma}\label{eq:clip-2}\end{equation}
其中$\gamma > 0$是一个常数。这两种方式都被视为梯度裁剪，总的来说就是控制更新量的模长不超过一个常数，第二种形式也跟RMSProp等自适应学习率优化器相关。此外，更精确地，我们有下面的不等式
\begin{equation}\frac{1}{2}\min\left\{1, \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert}\right\}\leq \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert+\gamma}\leq \min\left\{1, \frac{\gamma}{\Vert \nabla_{\theta} f(\theta)\Vert}\right\}\end{equation}
也就是说两者是可以相互控制的，所以其实两者基本是等价的。

L约束 #

有不少优化器相关的理论结果，在其证明中都假设了待优化函数$f(\theta)$的梯度满足如下的L约束：
\begin{equation}\Vert \nabla_{\theta} f(\theta + \Delta \theta) - \nabla_{\theta} f(\theta)\Vert\leq L\Vert \Delta\theta\Vert\label{eq:l-cond}\end{equation}
由于$\frac{\Vert \nabla_{\theta} f(\theta + \Delta \theta) - \nabla_{\theta} f(\theta)\Vert}{\Vert \Delta\theta\Vert}$是梯度的波动程度，实际上衡量的就是$f(\theta)$的光滑程度，所以上述约束也称为“L光滑性条件（L-smooth）”。

关于L约束，本博客也出现过多次，可以参考的文章有《深度学习中的Lipschitz约束：泛化与生成模型》、《BN究竟起了什么作用？一个闭门造车的分析》。值得提醒的是，不同的场景可能会需要不同的L约束，比如有时候我们要假设模型输出关于输入满足L约束，有时候我们要假设模型输出关于参数满足L约束，而上面假设的是模型loss的梯度关于参数满足L约束。

如果条件$\eqref{eq:l-cond}$成立，那么很多优化问题都将大大简化。因为我们可以证明（证明过程可参考这里）
\begin{equation}f(\theta+\Delta\theta) \leq f(\theta) + \left\langle \nabla_{\theta}f(\theta), \Delta\theta\right\rangle + \frac{1}{2}L \Vert \Delta\theta\Vert^2\label{eq:neq-1}\end{equation}
对于梯度下降来说，$\Delta\theta = -\eta \nabla_{\theta} f(\theta)$，代入上式得到
\begin{equation}f(\theta+\Delta\theta) \leq f(\theta) + \left(\frac{1}{2}L\eta^2 - \eta\right) \Vert \nabla_{\theta}f(\theta)\Vert^2\end{equation}
因此，为了保证每一步优化都使得$f(\theta)$下降，一个充分条件是$\frac{1}{2}L\eta^2 - \eta < 0$，即$\eta < \frac{2}{L}$，而$\frac{1}{2}L\eta^2 - \eta$的最小值在$\eta^* = \frac{1}{L} < \frac{2}{L}$时取到，所以只需要让学习率为$\frac{1}{L}$，那么每步迭代都可以使得$f(\theta)$下降，并且下降速度最快。

放松约束 #

条件$\eqref{eq:l-cond}$还可以带来很多漂亮的结果，然而问题是在很多实际优化问题中条件$\eqref{eq:l-cond}$并不成立，比如四次函数$f(\theta)=\theta^4$，这就导致了理论与实际的差距。而本文要介绍的论文，则引入了一个新的更宽松的约束：
\begin{equation}\Vert \nabla_{\theta} f(\theta + \Delta \theta) - \nabla_{\theta} f(\theta)\Vert\leq \left(L_0 + L_1\Vert \nabla_{\theta} f(\theta)\Vert\right)\Vert \Delta\theta\Vert\end{equation}
也就是将常数$L$换成动态的$L_0 + L_1\Vert \nabla_{\theta} f(\theta)\Vert$，原文称之为“(L₀, L₁)-smooth”，这里也称为“(L₀, L₁)约束”。显然这个条件就宽松多了，比如可以检验$\theta^4$是满足这个条件的，因此基于此条件所推导出的理论结果适用范围会更广。

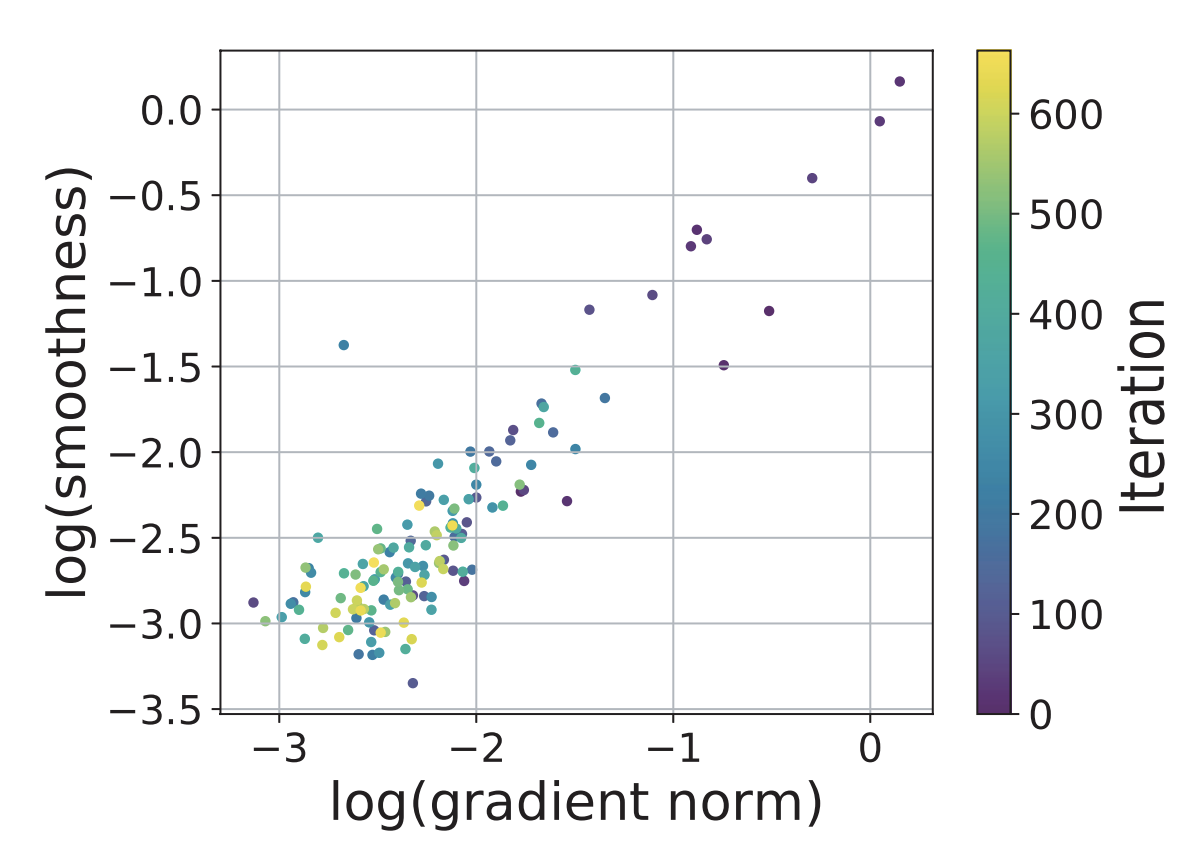
作者们是怎么提出这个条件的呢？论文说做实验观察出来的：

但笔者感觉吧，至少应该还有些从结果反推的成分在里边，不然谁那么无聊会去观察这两者的关系呢？

在新的约束之下，不等式$\eqref{eq:neq-1}$依旧是成立的，只不过$L$换成对应的动态项：
\begin{equation}f(\theta+\Delta\theta) \leq f(\theta) + \left\langle \nabla_{\theta}f(\theta), \Delta\theta\right\rangle + \frac{1}{2}\left(L_0 + L_1\Vert \nabla_{\theta} f(\theta)\Vert\right) \Vert \Delta\theta\Vert^2\end{equation}
代入$\Delta\theta = -\eta \nabla_{\theta} f(\theta)$得到
\begin{equation}f(\theta+\Delta\theta) \leq f(\theta) + \left(\frac{1}{2}\left(L_0 + L_1\Vert \nabla_{\theta} f(\theta)\Vert\right)\eta^2 - \eta\right) \Vert \nabla_{\theta}f(\theta)\Vert^2\end{equation}
所以很明显了，现在要保证每一步下降，那么就要求
\begin{equation}\eta < \frac{2}{L_0 + L_1\Vert \nabla_{\theta} f(\theta)\Vert}\end{equation}
以及最优学习率是
\begin{equation}\eta^* = \frac{1}{L_0 + L_1\Vert \nabla_{\theta} f(\theta)\Vert}\end{equation}
这就导出了梯度裁剪$\eqref{eq:clip-2}$。而保证了每一步都下降，那么就意味着在优化过程中每一步都没有做无用功，所以也就加速了训练过程。

文章小结 #

本文简要介绍了ICLR 2020的一篇分析梯度裁剪的满分论文，主要思路是引入了更宽松普适的假设条件，在新的条件下能体现出了梯度裁剪的必要性，并且由于放松了传统的约束，因此理论结果的适用范围更广，这也就表明，梯度裁剪确实是很多场景下都适用的技巧之一。

转载到请包括本文地址：https://kexue.fm/archives/7469

更详细的转载事宜请参考：《科学空间FAQ》