科学空间|Scientific Spaces

随着多模态LLM的方兴未艾，VQ（Vector Quantization）的地位也“水涨船高”，它可以作为视觉乃至任意模态的Tokenizer，将多模态数据统一到自回归生成框架中。遗憾的是，自VQ-VAE首次提出VQ以来，其理论并没有显著进步，像编码表的坍缩或利用率低等问题至今仍亟待解决，取而代之的是FSQ等替代方案被提出，成为了VQ有力的“竞争对手”。

然而，FSQ并不能在任何场景下都替代VQ，所以VQ本身的改进依然是有价值的。近日笔者读到了《Restructuring Vector Quantization with the Rotation Trick》，它提出了一种旋转技巧，声称能改善VQ的一系列问题，本文就让我们一起来品鉴一下。

回顾

早在五年前的博文《VQ-VAE的简明介绍：量子化自编码器》中我们就介绍过了VQ-VAE，后来在《简单得令人尴尬的FSQ：“四舍五入”超越了VQ-VAE》介绍FSQ的时候，也再次仔细地温习了VQ-VAE，还不了解的读者可以先阅读这两篇文章。

点击阅读全文...

弹簧

上一次我从密度的角度讨论了旋转的弹簧伸长的问题，由于对弹性形变等问题是初涉，所以花了好大功夫。这几天重新认识了一下胡克定律，并且从另外的角度给出了这道题目的一个相对简单的解法。在此把它记录下来，并写写我对弹性形变的一些粗浅看法。

在解答的过程中，我再次体验到了殊途同归的感觉，科学就是这样的奇妙，一个目的地往往有着不止一条道路，不同的道路会给我们不同的科学视觉，最终领略到不同的科学美景；多走几条路，更能够让我们从不同的角度领略美不胜收的科学，这也是众多旅游爱好者不辞千里地观赏美景的原因！

点击阅读全文...

我们考虑一个球状的星团，并假设它是各向同性的，即距离球心r处的物质密度ρ只与r有关，ρ=ρ(r)。那么，在半径为r的球形区域内的总质量为：
$$M(r)=\int_0^r 4\pi x^2 \rho(x) dx$$

想象有一颗质量比较小的恒星（其实相对于星团总质量，每一颗恒星的质量都很小）在星团的引力作用下运动（就好像太阳系绕着银河系运动一样），且恒星并没有受到其他物质（如星际尘埃等）的阻力。我们之前已经证明过，各向同性的球壳内部的引力是为0的，那么这种情况下的运动就相当于恒星只受到它到球心处的一个球形区域内的质量的引力吸引。根据万有引力定律，选择星团球心为参考系，可以得出
$$\ddot{\vec{r}}=-GM(r)\frac{\vec{r}}{r^3}$$

点击阅读全文...

量子力学中有一个很诡异的函数——Dirac函数，它似乎在物理的不少领域都有很大作用，它也具有明显的物理意义，但认真地看它却又感觉它根本就不是函数！这个“似而非是”的东西究竟是什么呢？让我们从一个物理问题引入：

设想一条质量为1，长度为$2l$的均匀直线，很显然直线的密度为$\rho=\frac{1}{2l}$；将直线的中点放置于坐标轴的原点，我们就有
$$\rho(x)=\left\{ \begin{array}{c}\frac{1}{2l} (-l \leq x \leq l)\\0 (x < -l , x > l)\end{array}\right.$$

所以有
$$\int_{-\infty}^{+\infty} \rho(x)dx=1$$

点击阅读全文...

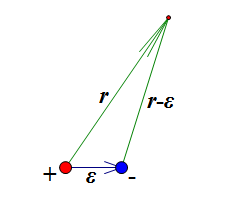
设想两个带有等量异号电荷的点电荷，它们之间的距离足够小，这样的一个模型被称为电偶极子（electric dipole）。我们研究电偶极子，主要是研究它在力学方面的性质。很多东西都可以用电偶极子来近似描述，比如一个小磁体周围的磁场，还有地球本身也可以近似看做一个偶极子来描述它的磁力情况，以及一些双原子分子的模型也被可以看做一个电偶极子模型，等等。在电偶极子模型中，两电荷的距离足够小，以至于我们忽略了一些关于距离的高次方项，只保留了线性部分，但对于物理探索来说，它已经足够精确，更重要的是，它足够简单，以至于我们可以容易把它清晰地描述出来。

我们先来研究电偶极子产生的电势。设它们各自的电荷量为q和-q，两者距离为ε，根据库仑定律，一个点电荷产生的电势，正比于该电荷的电荷量，同时反比于到该点电荷的距离。那么，一个电偶极子产生的电势为
$U=C(\frac{q}{r}+\frac{-q}{|\vec{r}-\vec{\varepsilon}|})$————(1)

点击阅读全文...

注：这是郝刘祥前辈的一篇论文，98年的时候发表在《自然辩证法通讯》上，里边讲述了费曼以及路径积分的相关故事。我从网上下载下来，原文是很粗糙的pdf文件，我特意将它转化为网页文件，供大家欣赏。有些公式很模糊，所以我已经到图书馆查找了原文，但是由于作者非理论物理专业人员，还不确定部分公式是否正确，请读者慎读。原文较长，将分开几篇来发。如果涉及到版权问题，请作者告之（bojone@spaces.ac.cn），我将会尽快处理掉。

自然辩证法通讯（JOURNAL OF DIALECTICS OF NATURE）
第二十卷总115期，1998第3期

郝刘祥

摘要：该文首先阐述了 Richard Feynman为解决经典电动力学的发散问题而做的艰苦努力，进而论述了这种努力的副产品何以使他偏爱作用量表述，以及他是如何在Dirac文章的启发下得到非相对论量子力学的第三种形式--作用量量子化方案的。文章的第三部分叙述了费曼将其方案推广到相对论情形的尝试和费曼图的由来。最后，该文试图就路径积分方法在量子场论等领域中的广泛应用以及费曼对量子场论的重大疑惑作一简要的说明。

关键词：费曼，作用量，几率幅，路径积分

点击阅读全文...

写在前头

经过两年多的开发，本站所用的Typecho终于发布了新版，虽然还是beta，但是我还是迫不及待地升级了。当然，前台并没有变化，但是几乎整个程序都是重构了的，后台也更加清爽了。本文是新版程度的第一篇文章，使用Markdowm语法编写。

----------

牛顿Vs胡克

在所有的力学系统中，最简单的或许就是简谐运动了。它由一个最简单的常系数线性微分方程组描述：
$$\ddot{\boldsymbol{x}}+\omega^2 \boldsymbol{x}=0$$

这也就是物体在弹性形变的胡克定律所描述的力的作用下的运动情况。我们可以很快用三角函数写出该方程的精确解。相比之下，二体问题的解就复杂多了，虽然二体问题也是精确可解的，但是显然没有简谐运动那样简单明了。然而，除了都是有心力之外，它们之间还有一个共同点，它们的运动轨道都是椭圆！（严格来说是圆锥曲线，因为还可能有抛物线跟双曲线，但是不失一般性，本文只分析椭圆轨道）两者之间是否存在着某种联系呢？如果可以将二体问题转变为简谐运动，那么分析过程应该可以大大化简了？

点击阅读全文...

最近一直在考虑一些自然语言处理问题和一些非线性分析问题，无暇总结发文，在此表示抱歉。本文要说的是对于一阶非线性差分方程（当然高阶也可以类似地做）的一种摄动格式，理论上来说，本方法可以得到任意一阶非线性差分方程的显式渐近解。

非线性差分方程

对于一般的一阶非线性差分方程
$$\begin{equation}\label{chafenfangcheng}x_{n+1}-x_n = f(x_n)\end{equation}$$
通常来说，差分方程很少有解析解，因此要通过渐近分析等手段来分析非线性差分方程的性质。很多时候，我们首先会考虑将差分替换为求导，得到微分方程
$$\begin{equation}\label{weifenfangcheng}\frac{dx}{dn}=f(x)\end{equation}$$
作为差分方程$\eqref{chafenfangcheng}$的近似。其中的原因，除了微分方程有比较简单的显式解之外，另一重要原因是微分方程$\eqref{weifenfangcheng}$近似保留了差分方程$\eqref{chafenfangcheng}$的一些比较重要的性质，如渐近性。例如，考虑离散的阻滞增长模型：
$$\begin{equation}\label{zuzhizengzhang}x_{n+1}=(1+\alpha)x_n -\beta x_n^2\end{equation}$$
对应的微分方程为（差分替换为求导）：
$$\begin{equation}\frac{dx}{dn}=\alpha x -\beta x^2\end{equation}$$
此方程解得
$$\begin{equation}x_n = \frac{\alpha}{\beta+c e^{-\alpha n}}\end{equation}$$
其中$c$是任意常数。上述结果已经大概给出了原差分方程$\eqref{zuzhizengzhang}$的解的变化趋势，并且成功给出了最终的渐近极限$x_n \to \frac{\alpha}{\beta}$。下图是当$\alpha=\beta=1$且$c=1$（即$x_0=\frac{1}{2}$）时，微分方程的解与差分方程的解的值比较。

差分方程的摄动法1

现在的问题是，既然微分方程的解可以作为一个形态良好的近似解了，那么是否可以在微分方程的解的基础上，进一步加入修正项提高精度？

点击阅读全文...