科学空间|Scientific Spaces

上一篇文章中，我们对原始的Sinusoidal位置编码做了较为详细的推导和理解，总的感觉是Sinusoidal位置编码是一种“想要成为相对位置编码的绝对位置编码”。一般来说，绝对位置编码具有实现简单、计算速度快等优点，而相对位置编码则直接地体现了相对位置信号，跟我们的直观理解吻合，实际性能往往也更好。由此可见，如果可以通过绝对位置编码的方式实现相对位置编码，那么就是“集各家之所长”、“鱼与熊掌兼得”了。Sinusoidal位置编码隐约做到了这一点，但并不够好。

本文将会介绍我们自研的Rotary Transformer（RoFormer）模型，它的主要改动是应用了笔者构思的“旋转式位置编码（Rotary Position Embedding，RoPE）”，这是一种配合Attention机制能达到“绝对位置编码的方式实现相对位置编码”的设计。而也正因为这种设计，它还是目前唯一一种可用于线性Attention的相对位置编码。

RoFormer：https://github.com/ZhuiyiTechnology/roformer

点击阅读全文...

一月份的时候，笔者写了《你可能不需要BERT-flow：一个线性变换媲美BERT-flow》，指出无监督语义相似度的SOTA模型BERT-flow其实可以通过一个简单的线性变换（白化操作，BERT-whitening）达到。随后，我们进一步完善了实验结果，写成了论文《Whitening Sentence Representations for Better Semantics and Faster Retrieval》。这篇博客将对这篇论文的内容做一个基本的梳理，并在5个中文语义相似度任务上进行了补充评测，包含了600多个实验结果。

Github链接：https://github.com/bojone/BERT-whitening

方法概要

BERT-whitening的思路很简单，就是在得到每个句子的句向量$\{x_i\}_{i=1}^N$后，对这些矩阵进行一个白化（也就是PCA），使得每个维度的均值为0、协方差矩阵为单位阵，然后保留$k$个主成分，流程如下图：

BERT-whitening的基本流程

点击阅读全文...

看过笔者之前的文章《线性Attention的探索：Attention必须有个Softmax吗？》和《Performer：用随机投影将Attention的复杂度线性化》的读者，可能会觉得本文的标题有点不自然，因为是先有线性Attention然后才有Performer的，它们的关系为“Performer是线性Attention的一种实现，在保证线性复杂度的同时保持了对标准Attention的近似”，所以正常来说是“从线性Attention到Performer”才对。

然而，本文并不是打算梳理线性Attention的发展史，而是打算反过来思考Performer给线性Attention所带来的启示，所以是“从Performer到线性Attention”。

激活函数

线性Attention的常见形式是
\begin{equation}Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V})_i = \frac{\sum\limits_{j=1}^n \text{sim}(\boldsymbol{q}_i, \boldsymbol{k}_j)\boldsymbol{v}_j}{\sum\limits_{j=1}^n \text{sim}(\boldsymbol{q}_i, \boldsymbol{k}_j)} = \frac{\sum\limits_{j=1}^n \phi(\boldsymbol{q}_i)^{\top} \varphi(\boldsymbol{k}_j)\boldsymbol{v}_j}{\sum\limits_{j=1}^n \phi(\boldsymbol{q}_i)^{\top} \varphi(\boldsymbol{k}_j)}\end{equation}

点击阅读全文...

今年年初，笔者受到BERT-flow的启发，构思了成为“BERT-whitening”的方法，并一度成为了语义相似度的新SOTA（参考《你可能不需要BERT-flow：一个线性变换媲美BERT-flow》，论文为《Whitening Sentence Representations for Better Semantics and Faster Retrieval》）。然而“好景不长”，在BERT-whitening提交到Arxiv的不久之后，Arxiv上出现了至少有两篇结果明显优于BERT-whitening的新论文。

第一篇是《Generating Datasets with Pretrained Language Models》，这篇借助模板从GPT2_XL中无监督地构造了数据对来训练相似度模型，个人认为虽然有一定的启发而且效果还可以，但是复现的成本和变数都太大。另一篇则是本文的主角《SimCSE: Simple Contrastive Learning of Sentence Embeddings》，它提出的SimCSE在英文数据上显著超过了BERT-flow和BERT-whitening，并且方法特别简单～

那么，SimCSE在中文上同样有效吗？能大幅提高中文语义相似度的效果吗？本文就来做些补充实验。

开源地址：https://github.com/bojone/SimCSE

点击阅读全文...

（注：本文的相关内容已整理成论文《Global Pointer: Novel Efficient Span-based Approach for Named Entity Recognition》，如需引用可以直接引用英文论文，谢谢。）

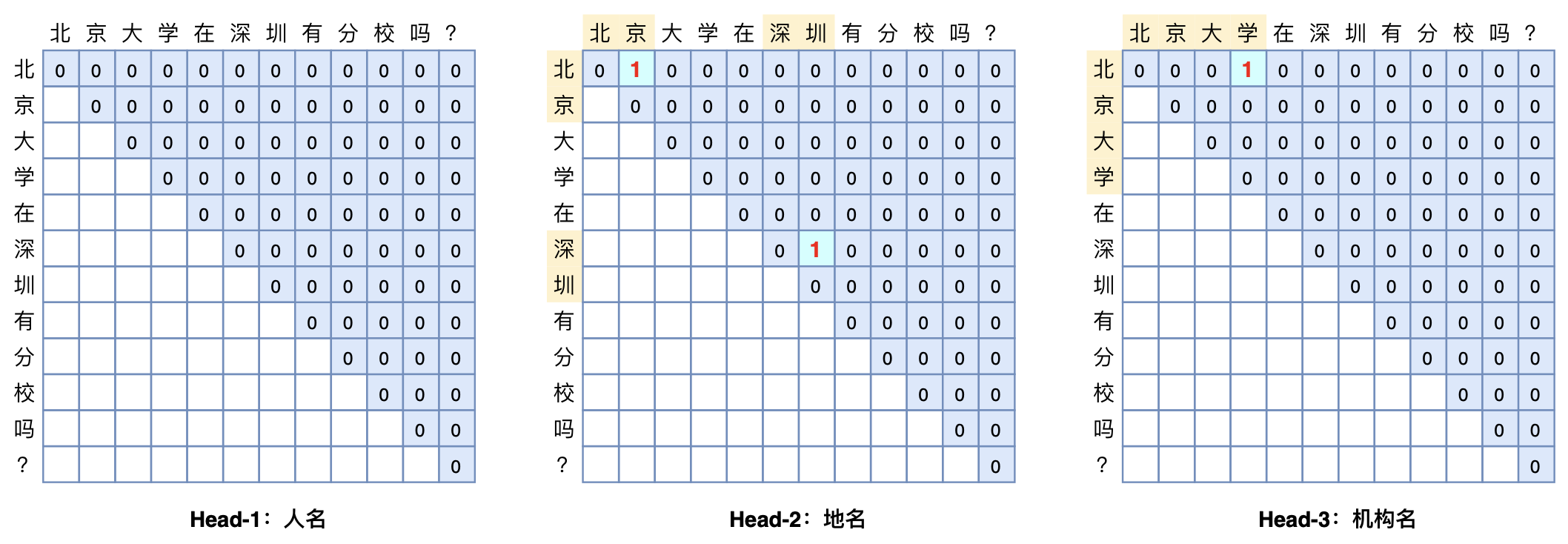
本文将介绍一个称为GlobalPointer的设计，它利用全局归一化的思路来进行命名实体识别（NER），可以无差别地识别嵌套实体和非嵌套实体，在非嵌套（Flat NER）的情形下它能取得媲美CRF的效果，而在嵌套（Nested NER）情形它也有不错的效果。还有，在理论上，GlobalPointer的设计思想就比CRF更合理；而在实践上，它训练的时候不需要像CRF那样递归计算分母，预测的时候也不需要动态规划，是完全并行的，理想情况下时间复杂度是$\mathcal{O}(1)$！

简单来说，就是更漂亮、更快速、更强大！真有那么好的设计吗？不妨继续看看。

GlobalPointer多头识别嵌套实体示意图

点击阅读全文...

在之前的文章《Transformer升级之路：2、博采众长的旋转式位置编码》中我们提出了旋转式位置编码RoPE以及对应的Transformer模型RoFormer。由于笔者主要研究的领域还是NLP，所以本来这个事情对于笔者来说已经完了。但是最近一段时间，Transformer模型在视觉领域也大火，各种Vision Transformer（ViT）层出不穷，于是就有了问题：二维情形的RoPE应该是怎样的呢？

咋看上去，这个似乎应该只是一维情形的简单推广，但其中涉及到的推导和理解却远比我们想象中复杂，本文就对此做一个分析，从而深化我们对RoPE的理解。

二维RoPE

什么是二维位置？对应的二维RoPE又是怎样的？它的难度在哪里？在这一节中，我们先简单介绍二维位置，然后直接给出二维RoPE的结果和推导思路，在随后的几节中，我们再详细给出推导过程。

点击阅读全文...

在《变分自编码器（五）：VAE + BN = 更好的VAE》中，我们讲到了NLP中训练VAE时常见的KL散度消失现象，并且提到了通过BN来使得KL散度项有一个正的下界，从而保证KL散度项不会消失。事实上，早在2018年的时候，就有类似思想的工作就被提出了，它们是通过在VAE中改用新的先验分布和后验分布，来使得KL散度项有一个正的下界。

该思路出现在2018年的两篇相近的论文中，分别是《Hyperspherical Variational Auto-Encoders》和《Spherical Latent Spaces for Stable Variational Autoencoders》，它们都是用定义在超球面的von Mises–Fisher（vMF）分布来构建先后验分布。某种程度上来说，该分布比我们常用的高斯分布还更简单和有趣～

KL散度消失

我们知道，VAE的训练目标是
\begin{equation}\mathcal{L} = \mathbb{E}_{x\sim \tilde{p}(x)} \Big[\mathbb{E}_{z\sim p(z|x)}\big[-\log q(x|z)\big]+KL\big(p(z|x)\big\Vert q(z)\big)\Big]
\end{equation}

点击阅读全文...

在之前的文章《最小熵原理（六）：词向量的维度应该怎么选择？》中，我们基于最小熵思想推导出了一个词向量维度公式“$n > 8.33\log N$”，然后在《让人惊叹的Johnson-Lindenstrauss引理：应用篇》中我们进一步指出，该结果与JL引理所给出的$\mathcal{O}(\log N)$是吻合的。

既然理论上看上去很完美，那么自然就有读者发问了：实验结果如何呢？8.33这个系数是最优的吗？本文就对此问题的相关内容做一个简单汇总。

词向量

首先，我们可以直接，当$N$为10万时，$8.33\log N\approx 96$，当$N$为500万时，$8.33\log N\approx 128$。这说明，至少在数量级上，该公式给出的结果是很符合我们实际所用维度的，因为在词向量时代，我们自行训练的词向量维度也就是100维左右。可能有读者会质疑，目前开源的词向量多数是300维的，像BERT的Embedding层都达到了768维，这不是明显偏离了你的结果了？

点击阅读全文...