23
Aug
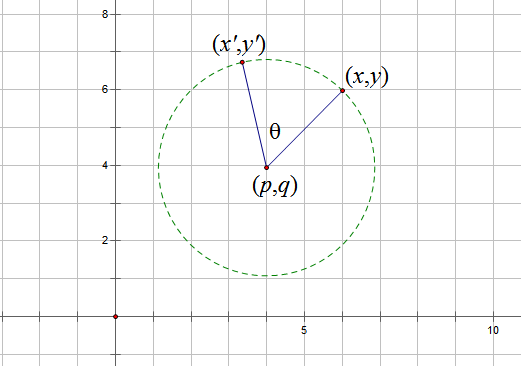
《向量》系列——4.天旋地转(向量,复数,极坐标)
By 苏剑林 | 2010-08-23 | 41953位读者 | 引用
2
Oct
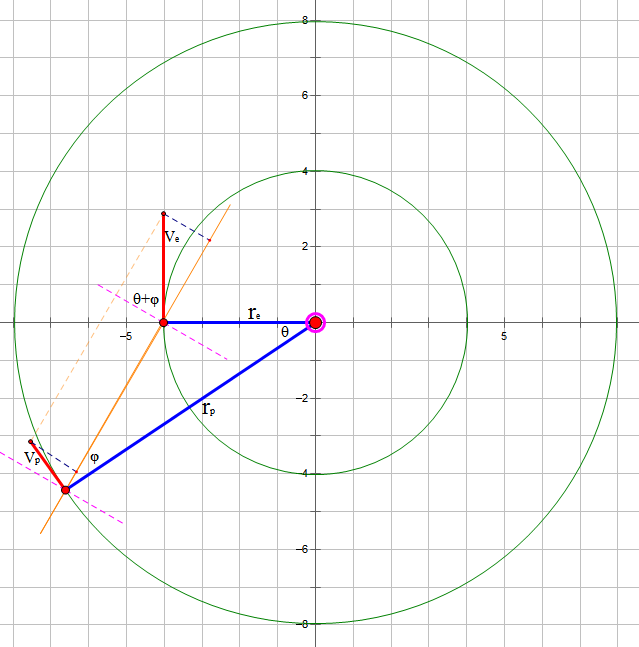
关于行星留周期的几何讨论
By 苏剑林 | 2010-10-02 | 18143位读者 | 引用
7
Nov
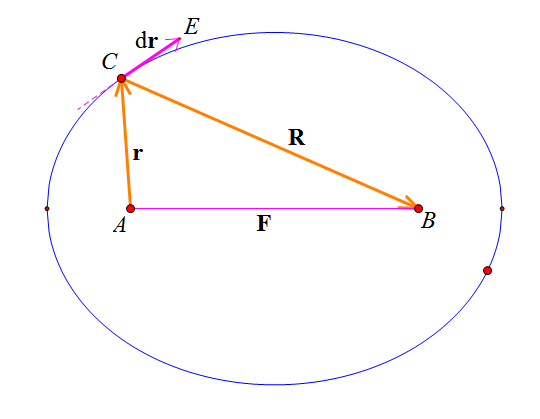
为什么是抛物线?——聚光面研究
By 苏剑林 | 2010-11-07 | 95442位读者 | 引用
13
Nov
意犹未尽——继续光学曲线
By 苏剑林 | 2010-11-13 | 56185位读者 | 引用
9
Jan
不可能事件——一道经典电磁感应题的错误
By 苏剑林 | 2011-01-09 | 45587位读者 | 引用
12
Mar
历史上的谜案——刘徽有没有使用外推法?
By 苏剑林 | 2011-03-12 | 32381位读者 | 引用话说当年我国古代数学家刘徽创立“割圆术”计算圆周率的事迹,在今天已被不少学生知晓;虽不能说家喻户晓,但是也为各教科书以及老师津津乐道。和古希腊的“数学之神”阿基米德同出一辙,刘徽也是使用圆的内接、外切正多边形来逼近圆形的;不一样的是,刘徽使用的方法是计算半径为1的圆的内接、外切正多边形的面积,而阿基米德计算的则是直径为1的圆的内接、外切正多边形的周长。两者的计算效果有什么区别呢?其实阿基米德的方法应该更快一点,阿基米德算到正n边形所得到的值,相当于刘徽算到正2n边形了。
在此我们不再对两者的计算方法进行区分,因为两者的本质都是一样的。按照现代数学的写法,“割圆术”的理论依据是
$$lim_{n\to \infty} n \sin(\frac{\pi}{n})=\pi\tag{1}$$
当然,刘徽不可能有现代计算正弦函数值的公式(现在计算正弦函数值一般用泰勒级数展开,而泰勒级数展开需要用到$\pi$的值),甚至在他那个时代就连笔墨也没有,据我所知即使是后来的祖冲之推算圆周率时,唯一的计算工具也只是现在称为“算筹”的小棍。不过刘徽还是凭借着超强的毅力,利用递推的方法逐步求圆周率。
23
Apr











最近评论