从DCGAN到SELF-MOD:GAN的模型架构发展一览
By 苏剑林 | 2019-04-19 | 79079位读者 | 引用事实上,O-GAN的发现,已经达到了我对GAN的理想追求,使得我可以很惬意地跳出GAN的大坑了。所以现在我会试图探索更多更广的研究方向,比如NLP中还没做过的任务,又比如图神经网络,又或者其他有趣的东西。
不过,在此之前,我想把之前的GAN的学习结果都记录下来。
这篇文章中,我们来梳理一下GAN的架构发展情况,当然主要的是生成器的发展,判别器一直以来的变动都不大。还有,本文介绍的是GAN在图像方面的模型架构发展,跟NLP的SeqGAN没什么关系。
此外,关于GAN的基本科普,本文就不再赘述了。
漫谈重参数:从正态分布到Gumbel Softmax
By 苏剑林 | 2019-06-10 | 222174位读者 | 引用最近在用VAE处理一些文本问题的时候遇到了对离散形式的后验分布求期望的问题,于是沿着“离散分布 + 重参数”这个思路一直搜索下去,最后搜到了Gumbel Softmax,从对Gumbel Softmax的学习过程中,把重参数的相关内容都捋了一遍,还学到一些梯度估计的新知识,遂记录在此。
文章从连续情形出发开始介绍重参数,主要的例子是正态分布的重参数;然后引入离散分布的重参数,这就涉及到了Gumbel Softmax,包括Gumbel Softmax的一些证明和讨论;最后再讲讲重参数背后的一些故事,这主要跟梯度估计有关。
基本概念
重参数(Reparameterization)实际上是处理如下期望形式的目标函数的一种技巧:
\begin{equation}L_{\theta}=\mathbb{E}_{z\sim p_{\theta}(z)}[f(z)]\label{eq:base}\end{equation}
这样的目标在VAE中会出现,在文本GAN也会出现,在强化学习中也会出现($f(z)$对应于奖励函数),所以深究下去,我们会经常碰到这样的目标函数。取决于$z$的连续性,它对应不同的形式:
\begin{equation}\int p_{\theta}(z) f(z)dz\,\,\,\text{(连续情形)}\qquad\qquad \sum_{z} p_{\theta}(z) f(z)\,\,\,\text{(离散情形)}\end{equation}
当然,离散情况下我们更喜欢将记号$z$换成$y$或者$c$。
为节约而生:从标准Attention到稀疏Attention
By 苏剑林 | 2019-07-27 | 129506位读者 | 引用如今NLP领域,Attention大行其道,当然也不止NLP,在CV领域Attention也占有一席之地(Non Local、SAGAN等)。在18年初《〈Attention is All You Need〉浅读(简介+代码)》一文中,我们就已经讨论过Attention机制,Attention的核心在于$\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}$三个向量序列的交互和融合,其中$\boldsymbol{Q},\boldsymbol{K}$的交互给出了两两向量之间的某种相关度(权重),而最后的输出序列则是把$\boldsymbol{V}$按照权重求和得到的。
显然,众多NLP&CV的成果已经充分肯定了Attention的有效性。本文我们将会介绍Attention的一些变体,这些变体的共同特点是——“为节约而生”——既节约时间,也节约显存。
背景简述
《Attention is All You Need》一文讨论的我们称之为“乘性Attention”,目前用得比较广泛的也就是这种Attention:
\begin{equation}Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = softmax\left(\frac{\boldsymbol{Q}\boldsymbol{K}^{\top}}{\sqrt{d_k}}\right)\boldsymbol{V}\end{equation}
从几何视角来理解模型参数的初始化策略
By 苏剑林 | 2020-01-16 | 92117位读者 | 引用对于复杂模型来说,参数的初始化显得尤为重要。糟糕的初始化,很多时候已经不单是模型效果变差的问题了,还更有可能是模型根本训练不动或者不收敛。在深度学习中常见的自适应初始化策略是Xavier初始化,它是从正态分布$\mathcal{N}\left(0,\frac{2}{fan_{in} + fan_{out}}\right)$中随机采样而构成的初始权重,其中$fan_{in}$是输入的维度而$fan_{out}$是输出的维度。其他初始化策略基本上也类似,只不过假设有所不同,导致最终形式略有差别。
标准的初始化策略的推导是基于概率统计的,大概的思路是假设输入数据的均值为0、方差为1,然后期望输出数据也保持均值为0、方差为1,然后推导出初始变换应该满足的均值和方差条件。这个过程理论上没啥问题,但在笔者看来依然不够直观,而且推导过程的假设有点多。本文则希望能从几何视角来理解模型的初始化方法,给出一个更直观的推导过程。
信手拈来的正交
前者时间笔者写了《n维空间下两个随机向量的夹角分布》,其中的一个推论是
推论1: 高维空间中的任意两个随机向量几乎都是垂直的。
从EMD、WMD到WRD:文本向量序列的相似度计算
By 苏剑林 | 2020-05-13 | 57790位读者 | 引用在NLP中,我们经常要去比较两个句子的相似度,其标准方法是想办法将句子编码为固定大小的向量,然后用某种几何距离(欧氏距离、$\cos$距离等)作为相似度。这种方案相对来说比较简单,而且检索起来比较快速,一定程度上能满足工程需求。
此外,还可以直接比较两个变长序列的差异性,比如编辑距离,它通过动态规划找出两个字符串之间的最优映射,然后算不匹配程度;现在我们还有Word2Vec、BERT等工具,可以将文本序列转换为对应的向量序列,所以也可以直接比较这两个向量序列的差异,而不是先将向量序列弄成单个向量。
后一种方案速度相对慢一点,但可以比较得更精细一些,并且理论比较优雅,所以也有一定的应用场景。本文就来简单介绍一下属于后者的两个相似度指标,分别简称为WMD、WRD。
Earth Mover's Distance
本文要介绍的两个指标都是以Wasserstein距离为基础,这里会先对它做一个简单的介绍,相关内容也可以阅读笔者旧作《从Wasserstein距离、对偶理论到WGAN》。Wasserstein距离也被形象地称之为“推土机距离”(Earth Mover's Distance,EMD),因为它可以用一个“推土”的例子来通俗地表达它的含义。
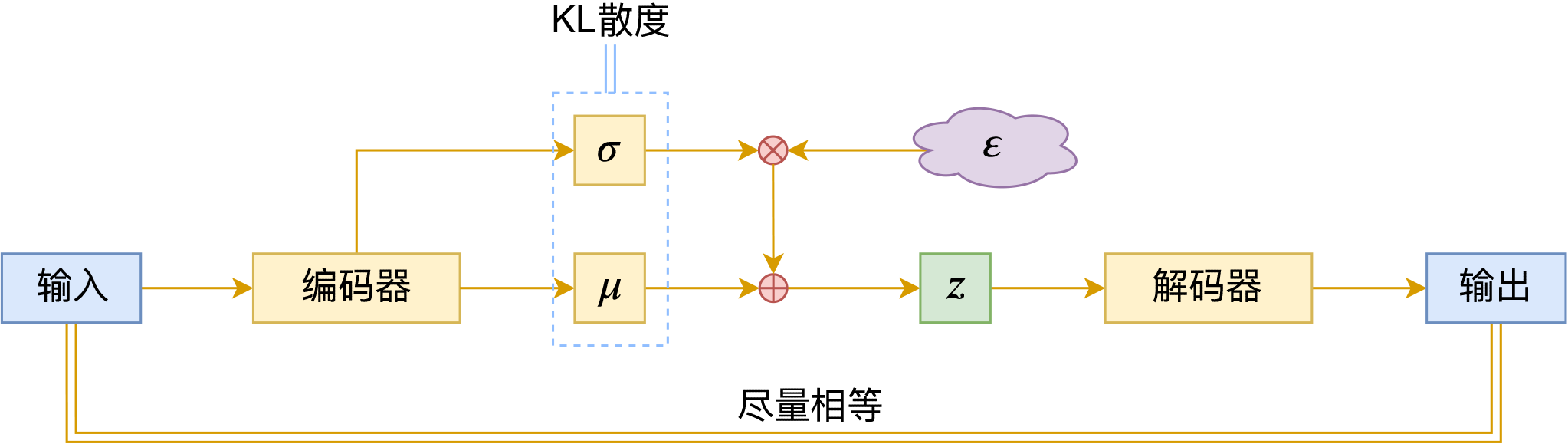
变分自编码器(六):从几何视角来理解VAE的尝试
By 苏剑林 | 2020-09-10 | 66274位读者 | 引用前段时间公司组织技术分享,轮到笔者时,大家希望我讲讲VAE。鉴于之前笔者也写过变分自编码器系列,所以对笔者来说应该也不是特别难的事情,因此就答应了下来,后来仔细一想才觉得犯难:怎么讲才好呢?
对于VAE来说,之前笔者有两篇比较系统的介绍:《变分自编码器(一):原来是这么一回事》和《变分自编码器(二):从贝叶斯观点出发》。后者是纯概率推导,对于不做理论研究的人来说其实没什么意义,也不一定能看得懂;前者虽然显浅一点,但也不妥,因为它是从生成模型的角度来讲的,并没有说清楚“为什么需要VAE”(说白了,VAE可以带来生成模型,但是VAE并不一定就为了生成模型),整体风格也不是特别友好。
笔者想了想,对于大多数不了解但是想用VAE的读者来说,他们应该只希望大概了解VAE的形式,然后想要知道“VAE有什么作用”、“VAE相比AE有什么区别”、“什么场景下需要VAE”等问题的答案,对于这种需求,上面两篇文章都无法很好地满足。于是笔者尝试构思了VAE的一种几何图景,试图从几何角度来描绘VAE的关键特性,在此也跟大家分享一下。
泛化性乱弹:从随机噪声、梯度惩罚到虚拟对抗训练
By 苏剑林 | 2020-06-01 | 96216位读者 | 引用提高模型的泛化性能是机器学习致力追求的目标之一。常见的提高泛化性的方法主要有两种:第一种是添加噪声,比如往输入添加高斯噪声、中间层增加Dropout以及进来比较热门的对抗训练等,对图像进行随机平移缩放等数据扩增手段某种意义上也属于此列;第二种是往loss里边添加正则项,比如$L_1, L_2$惩罚、梯度惩罚等。本文试图探索几种常见的提高泛化性能的手段的关联。
随机噪声
我们记模型为$f(x)$,$\mathcal{D}$为训练数据集合,$l(f(x), y)$为单个样本的loss,那么我们的优化目标是
\begin{equation}\mathop{\text{argmin}}_{\theta} L(\theta)=\mathbb{E}_{(x,y)\sim \mathcal{D}}[l(f(x), y)]\end{equation}
$\theta$是$f(x)$里边的可训练参数。假如往模型输入添加噪声$\varepsilon$,其分布为$q(\varepsilon)$,那么优化目标就变为
\begin{equation}\mathop{\text{argmin}}_{\theta} L_{\varepsilon}(\theta)=\mathbb{E}_{(x,y)\sim \mathcal{D}, \varepsilon\sim q(\varepsilon)}[l(f(x + \varepsilon), y)]\end{equation}
当然,可以添加噪声的地方不仅仅是输入,也可以是中间层,也可以是权重$\theta$,甚至可以是输出$y$(等价于标签平滑),噪声也不一定是加上去的,比如Dropout是乘上去的。对于加性噪声来说,$q(\varepsilon)$的常见选择是均值为0、方差固定的高斯分布;而对于乘性噪声来说,常见选择是均匀分布$U([0,1])$或者是伯努利分布。
添加随机噪声的目的很直观,就是希望模型能学会抵御一些随机扰动,从而降低对输入或者参数的敏感性,而降低了这种敏感性,通常意味着所得到的模型不再那么依赖训练集,所以有助于提高模型泛化性能。
从采样看优化:可导优化与不可导优化的统一视角
By 苏剑林 | 2020-06-23 | 54764位读者 | 引用不少读者都应该知道,损失函数与评测指标的不一致性是机器学习的典型现象之一,比如分类问题中损失函数用交叉熵,评测指标则是准确率或者F1,又比如文本生成中损失函数是teacher-forcing形式的交叉熵,评测指标则是BLEU、ROUGE等。理想情况下,当然是评测什么指标,我们就去优化这个指标,然而评测指标通常都是不可导的,而我们多数都是使用基于梯度的优化器,这就要求最小化的目标必须是可导的,这是不一致性的来源。
前些天在arxiv刷到了一篇名为《MLE-guided parameter search for task loss minimization in neural sequence modeling》的论文,顾名思义,它是研究如何直接优化文本生成的评测指标的。经过阅读,笔者发现这篇论文很有价值,事实上它提供了一种优化评测指标的新思路,适用范围并不局限于文本生成中。不仅如此,它甚至还包含了一种理解可导优化与不可导优化的统一视角。
采样视角
首先,我们可以通过采样的视角来重新看待优化问题:设模型当前参数为$\theta$,优化目标为$l(\theta)$,我们希望决定下一步的更新量$\Delta\theta$,为此,我们先构建分布
\begin{equation}p(\Delta\theta|\theta)=\frac{e^{-[l(\theta + \Delta\theta) - l(\theta)]/\alpha}}{Z(\theta)},\quad Z(\theta) = \int e^{-[l(\theta + \Delta\theta) - l(\theta)]/\alpha} d(\Delta\theta)\end{equation}










最近评论