【宇宙驿站】拼音输入法天文学词库
By 苏剑林 | 2009-11-11 | 19788位读者 | 引用宇宙驿站定于本周五更换服务器
By 苏剑林 | 2010-07-21 | 15668位读者 | 引用宇宙驿站服务器升级完毕
By 苏剑林 | 2014-01-19 | 33813位读者 | 引用路径积分系列:1.我的毕业论文
By 苏剑林 | 2016-05-30 | 31203位读者 | 引用之前承诺过会把毕业论文共享出来,让大家批评指正,却一直偷懒没动。事实上,毕业论文的主要内容就是路径积分的一些入门级别的内容,标题为《随机游走、随机微分方程与偏微分方程的路径积分方法》。我的摘要是这样写的:
本文从随机游走模型出发,得到了关于随机游走模型的一般结果;然后基于随机游走模型引入了路径积分,并且通过路径积分方法,实现了随机游走、随机微分方程与抛物型微分方程的相互转化,并给出了一些计算案例.
路径积分方法是量子理论的一种形式,但实际上它可以抽象为一个有用的数学工具,本文的主要方法正是抽象后的路径积分;其次,量子力学中有一个相当典型的抛物型偏微分方程——薛定谔方程,物理学家已经对它进行了大量的研究,有众多的成果;而随机微分方程是一个微分方程的拓展,在物理、工程、金融等很多方面都有重要应用,这个领域中也有很多研究方法;最后,随机游走是一个简单而重要的模型,它是很多扩散模型的基础,而且具有容易使用计算机模拟的特性. 因此,实现三者的转化是很有意义的.
本文有一些新的内容,比如现有文献比较少研究的不对称随机游走方面、以及现有文献比较含糊的对路径积分的介绍等,可以供同好参考,希望借此方式,能够让一些读者以更简洁明了的方式理解路径积分. 但是本文主要是陈述性的,旨在在国内推广路径积分方法. 在国外,路径积分方法得到了相当的重视,它源于量子力学,但应用已经不仅仅限于量子力学,如著作[1],因此,推广路径积分方法、增加路径积分的中文资料,是很有意义和很有必要的事情.
本文所有推导和例子均以一维为例,相应的多维问题可以类似地计算。
生成扩散模型漫谈(十七):构建ODE的一般步骤(下)
By 苏剑林 | 2023-02-23 | 104557位读者 | 引用历史总是惊人地相似。当初笔者在写《生成扩散模型漫谈(十四):构建ODE的一般步骤(上)》(当时还没有“上”这个后缀)时,以为自己已经搞清楚了构建ODE式扩散的一般步骤,结果读者 @gaohuazuo 就给出了一个新的直观有效的方案,这直接导致了后续《生成扩散模型漫谈(十四):构建ODE的一般步骤(中)》(当时后缀是“下”)。而当笔者以为事情已经终结时,却发现ICLR2023的论文《Flow Straight and Fast: Learning to Generate and Transfer Data with Rectified Flow》又给出了一个构建ODE式扩散模型的新方案,其简洁、直观的程度简直前所未有,令人拍案叫绝。所以笔者只好默默将前一篇的后缀改为“中”,然后写了这个“下”篇来分享这一新的结果。
直观结果
我们知道,扩散模型是一个$\boldsymbol{x}_T\to \boldsymbol{x}_0$的演化过程,而ODE式扩散模型则指定演化过程按照如下ODE进行:
\begin{equation}\frac{d\boldsymbol{x}_t}{dt}=\boldsymbol{f}_t(\boldsymbol{x}_t)\label{eq:ode}\end{equation}
而所谓构建ODE式扩散模型,就是要设计一个函数$\boldsymbol{f}_t(\boldsymbol{x}_t)$,使其对应的演化轨迹构成给定分布$p_T(\boldsymbol{x}_T)$、$p_0(\boldsymbol{x}_0)$之间的一个变换。说白了,我们希望从$p_T(\boldsymbol{x}_T)$中随机采样一个$\boldsymbol{x}_T$,然后按照上述ODE向后演化得到的$\boldsymbol{x}_0$是$\sim p_0(\boldsymbol{x}_0)$的。
欲对接广义相对论,新量子引力模型能否成功?
By 苏剑林 | 2009-09-05 | 18432位读者 | 引用时至目前为止,理论物理上最深奥的问题之一,就是调和广义相对论与量子力学,而一个令物理学家们无比兴奋的,同时也争论不休的量子引力新模型,是否能重新书写物理学理论?针对不久前诞生于美国劳伦斯伯克利实验室的“霍扎瓦模型”,美国得克萨斯A&M大学科学家对其进一步研究后得出中肯的结论,并将结果与值得商榷的内容发表于8月24日出版的《物理评论快报》杂志。
量子引力的新曙光
量子引力主要就是尝试将量子力学与广义相对论合并在一起,描述对重力场进行量子化,属于万有理论之一隅。但应该如何结合,又如何让二者在微观长度等级下维持正确性,以及任何候选的量子引力论又能提供什么样可证实的预测,这是当前的物理学悬而未决的问题。遗憾的是,量子引力所探讨的能量与尺度,乃是此前实验室条件下无法观测得到的,尽管可能,且可以透过天文观测来检验,但仍属少数特例,关于量子引力理论发展上的提示一直未能成功。
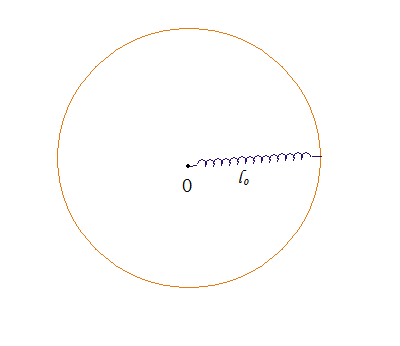
旋转的弹簧将如何伸长?
By 苏剑林 | 2010-07-30 | 104635位读者 | 引用未来的天地枢纽——太空天梯
By 苏剑林 | 2010-10-22 | 25921位读者 | 引用漫话
BoJone认为,科学的意义并非在于无休止地计算,而是利用有限的科学理论来解释尽可能多的自然、生活现象。正因如此,科学家们追求和谐、简洁、优美的科学理论。科学就是想方设法地把未知变成已知,并在此基础上进一步发展。
随着媒体技术的发展,我们接触信息的渠道越来越多。每每我们从互联网或报纸上看到一则科学新闻时,我们几乎都会为之兴奋。但是,外行看热闹,内行看门道。对于真正热爱科学的朋友来说,也许会更加感兴趣新闻内容的来由。也就是说,我们希望进一步了解结论是怎样得出来的——哪怕只是在很浅的层面上认识。









最近评论