24
Oct
扬帆——在宇宙的海洋中航行
By 苏剑林 | 2010-10-24 | 23790位读者 | 引用
9
Apr
趣题:与橡皮绳赛跑的蚂蚁
By 苏剑林 | 2014-04-09 | 33726位读者 | 引用
19
Jul
三次方程的根式求解(通俗版本)
By 苏剑林 | 2009-07-19 | 65966位读者 | 引用
4
Apr
数值方法解方程之终极算法
By 苏剑林 | 2010-04-04 | 49344位读者 | 引用呵呵,做了一回标题党,可能说得夸张了一点。说是“终极算法”,主要是因为它可以任意提高精度、而且几乎可以应付任何非线性方程(至少理论上是这样),提高精度是已知的迭代式上添加一些项,而不是完全改变迭代式的形式,当然在提高精度的同时,计算量也会随之增大。其理论基础依旧是泰勒级数。
我们考虑方程$x=f(y)$,已知y求x是很容易的,但是已知x求y并不容易。我们考虑把y在$(x_0,y_0)$处展开成x的的泰勒级数。关键是求出y的n阶导数$\frac{d^n y}{dx^n}$。我们记$f^{(n)}(y)=\frac{d^n x}{dy^n}$,并且有
$$\frac{dy}{dx}=\frac{1}{(\frac{dx}{dy})}=f'(y)^{-1}$$
6
Feb
直上云霄的无穷指数方程
By 苏剑林 | 2010-02-06 | 32327位读者 | 引用
27
Feb
“n次方程有n个根”的证明
By 苏剑林 | 2010-02-27 | 75805位读者 | 引用
9
Aug
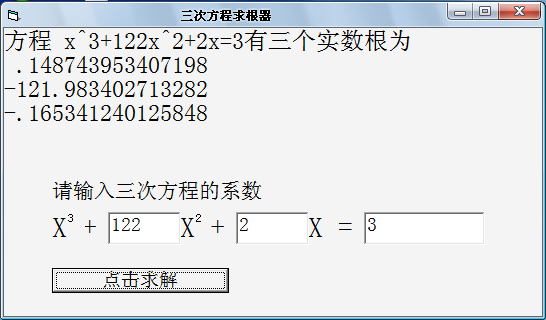
三次方程求根器(VB程序+源码,“低手”拙作)
By 苏剑林 | 2010-08-09 | 34906位读者 | 引用
9
Aug










最近评论