一月份的时候，笔者写了《你可能不需要BERT-flow：一个线性变换媲美BERT-flow》，指出无监督语义相似度的SOTA模型BERT-flow其实可以通过一个简单的线性变换（白化操作，BERT-whitening）达到。随后，我们进一步完善了实验结果，写成了论文《Whitening Sentence Representations for Better Semantics and Faster Retrieval》。这篇博客将对这篇论文的内容做一个基本的梳理，并在5个中文语义相似度任务上进行了补充评测，包含了600多个实验结果。

方法概要 #

BERT-whitening的思路很简单，就是在得到每个句子的句向量$\{x_i\}_{i=1}^N$后，对这些矩阵进行一个白化（也就是PCA），使得每个维度的均值为0、协方差矩阵为单位阵，然后保留$k$个主成分，流程如下图：

BERT-whitening的基本流程

BERT-whitening的基本流程

当然，理论上来说，我们也可以将BERT-whitening看成是BERT-flow的最简单实现，而之前的博客中已经指出，就是这样简单的实现足以媲美一般的BERT-flow模型，有时候甚至更好。同时，BERT-whitening在变换的同时还对特征重要性进行了排序，因此我们可以对句向量进行降维来提高检索速度。实验结果显示，在多数任务中，降维不但不会带来效果上的下降，反而会带来效果上的提升。

英文任务 #

首先介绍BERT-whitening在英文任务上的测试结果，主要包含三个图表，基本上实现了与BERT-flow进行了严格对照。

纯无监督 #

首先，第一个表格介绍的是在完全无监督的情况下，直接使用预训练的BERT抽取句向量的结果。在BERT-flow的论文中，我们已经确实，如果不加任何后处理手段，那么基于BERT抽取句向量的最好Pooling方法是BERT的第一层与最后一层的所有token向量的平均，即fisrt-larst-avg（BERT-flow论文误认为是最后两层的平均，记为了last2avg，实际上是第一层与最后一层）。所以后面的结果，都是以fisrt-larst-avg为基准来加flow或者whitening。

英文任务上纯无监督语义匹配的评测结果

英文任务上纯无监督语义匹配的评测结果

NLI监督 #

然后，第二个表格介绍的是基于NLI数据集微调后的Sentence-BERT模型（SBERT）抽取句向量的结果，在此情况下同样是fisrt-larst-avg最好，所以flow和whitening的基准都是fisrt-larst-avg出来的句向量。NLI数据集是自然语言推理数据集，跟语义相似度类似但不等价，它可以作为语义相似度任务的有监督预训练，但由于没有直接用到语义相似度数据，因此相对于语义相似度任务来说依然属于无监督的。

英文任务上基于BERT-NLI的语义匹配的评测结果

英文任务上基于BERT-NLI的语义匹配的评测结果

维度-效果 #

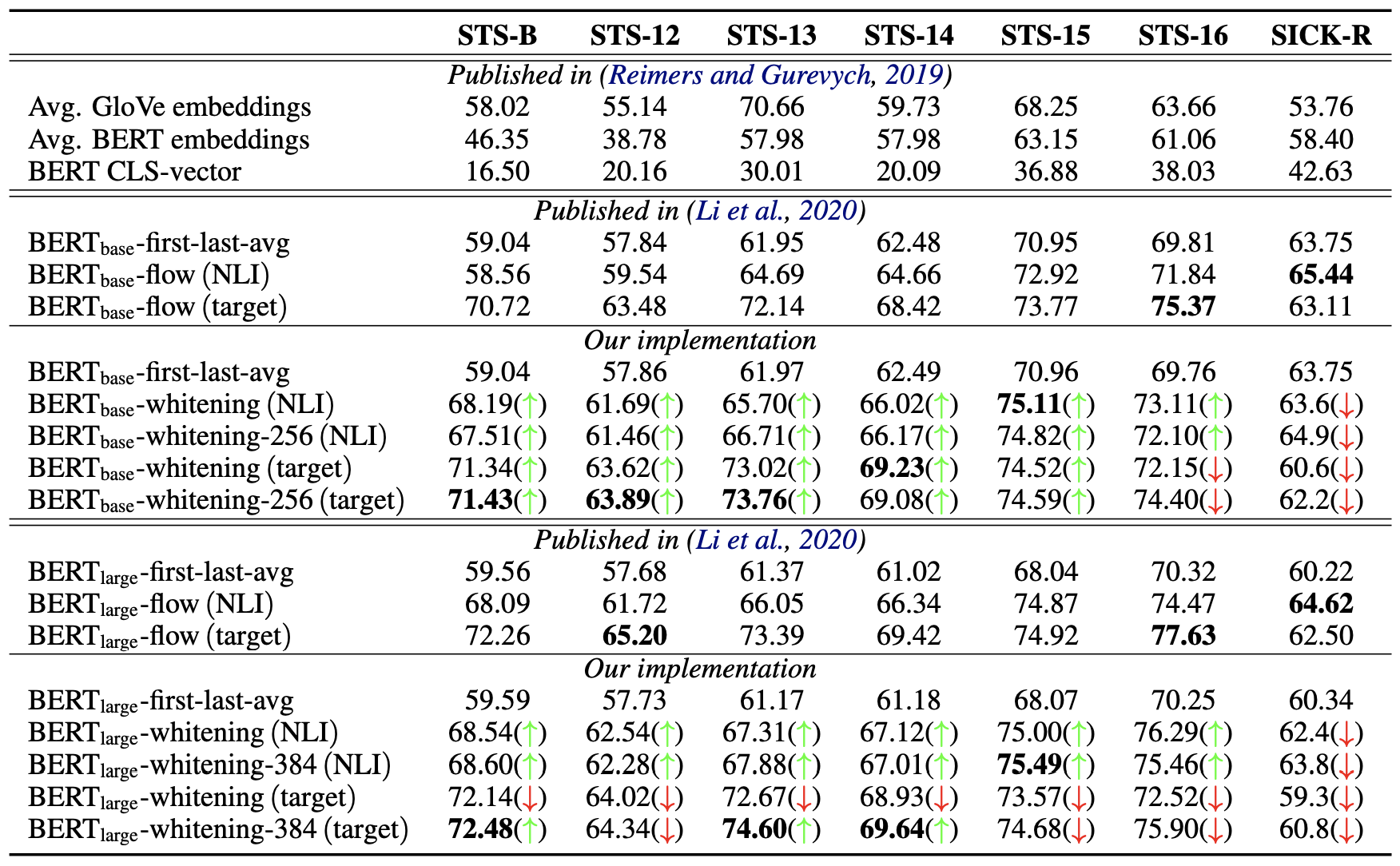
在这两个表格中，加粗的是最优结果；绿色箭头$\color{green}{\uparrow}$意味着BERT-whitening的结果优于同样情况下的BERT-flow模型，而红色箭头$\color{red}{\downarrow}$则相反，也就是说，绿色箭头越多意味着BERT-whitening的效果也好；whitening后面接的数字256、384指的是降维后保留的维度。所以，从这两个表格可以看出，BERT-whitening总体而言优于BERT-flow，实现了大多数任务的SOTA，并且多数情况下，降维还能进一步提升效果。

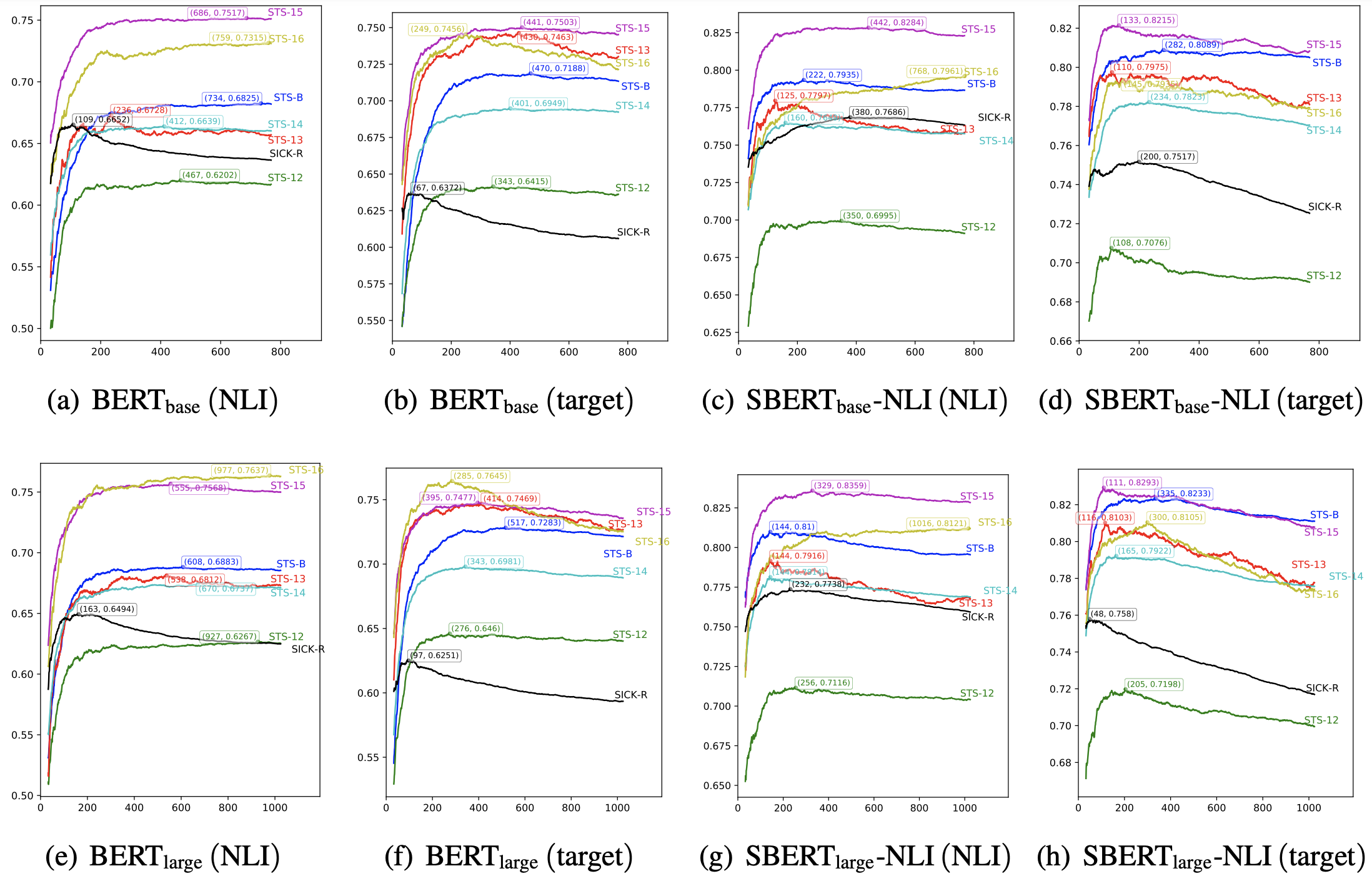
为了进一步确认降维所带来的效果，我们绘制了如下的保留维度与效果关系图：

英文各个任务上的“维度-效果”图，图中还标记了最有效果对应的维度，可以看到对于每个任务而言，降维都有可能带来一定的提升。

英文各个任务上的“维度-效果”图，图中还标记了最有效果对应的维度，可以看到对于每个任务而言，降维都有可能带来一定的提升。

上图演示了各个模型在各个任务上经过whitening之后，保留的维度与评测指标的变化曲线。可以看到，对于每个任务来说，最优效果都不是在全部维度取到，这意味着降维都可以带来一定的效果提升，并且可以看到，不少任务甚至可以降维到原来的1/8甚至更多而保持效果不减甚至增加，这充分显示了BERT-whitening的工程价值，因为降维意味着我们能大大加快检索速度。

中文任务 #

秉承着“没有在中文测试过的模型是没有灵魂的”的理念，笔者整理了一些中文语义相似度数据集，结合不同的中文预训练模型、Pooling方式以及whitening与否进行了评测，结果汇总于此，供大家对比。

评测情况 #

本次评测涉及到11个模型、5个数据集、4种Pooling方式，每种组合比较“不whitening”、“whitening”、“whitening且降维”3种后处理方式的效果，所以共有将近
$$11\times 5\times 4\times 3 = 660$$
个实验结果，算是比较全面了。说“将近”是因为某些Pooling方式在某些模型不可用，所以离660还差一点。由于BERT-flow计算成本明显大于BERT-whitening，因此我们没有复现对比BERT-flow的效果，但是从英文任务上可以看出，BERT-whitening和BERT-flow的效果通常是接近的，并且BERT-whitening通常还优于BERT-flow，因为whitening的效果应该是有代表性的了。

评测指标跟前述英文任务一样，都是用spearman相关系数，这是一个类似AUC的排序指标，只依赖于预测分数的顺序，并且不依赖于阈值，所以用来评测效果是比较适合的。之所以没有用大家更熟悉的准确率（accuracy）指标，一是因为准确率依赖于具体的阈值，二是因为STS-B数据集的标签是1～5的数字，并不是0/1标签，要算准确率也无从算起，因此统一用spearman相关系数了。如果读者非要从准确率角度理解，那么大概可以认为“accuracy ≈ 0.5 + spearman / 2”吧。

其中11个模型如下：

BERT：Google开源的中文BERT base版，链接；

RoBERTa：哈工大开源的roberta_wwm_ext的base版，链接；

NEZHA：华为开源的相对位置编码的BERT base版（wwm），链接；

WoBERT：以词为单位的BERT，这里用的是Plus版，链接；

RoFormer：加入了新型位置编码的BERT，链接；

BERTlarge：腾讯UER开源的BERT large版本，链接；

RoBERTalarge：哈工大开源的roberta_wwm_ext的large版，链接；

NEZHA-large：华为开源的相对位置编码的BERT large版（wwm），链接；

SimBERT：经过相似句训练的BERT base版，链接；

SimBERTsmall：经过相似句训练的BERT small版，链接；

SimBERTtiny：经过相似句训练的BERT tiny版，链接。

5个任务如下：

ATEC：ATEC语义相似度学习赛数据集，金融领域客服场景，原比赛链接已经失效，当前数据来自链接；

BQ：哈工大BQ Corpus数据集，银行金融领域的问题匹配，详情可看链接；

LCQMC：哈工大LCQMC数据集，覆盖多个领域的问题匹配，详情可看链接；

PAWSX：谷歌发布的数据集（链接），数据集里包含了多语种的释义对和非释义对，即识别一对句子是否具有相同的释义（含义），特点是具有高度重叠词汇，对无监督方法来说算是比较难的任务，这里只保留了中文部分；

STS-B：计算两句话之间的相关性，原数据集为英文版，通过翻译加部分人工修正的方法生成中文版，来源链接。

4种Pooling方式如下：

P1：把encoder的最后一层的[CLS]向量拿出来；

P2：把Pooler（BERT用来做NSP任务）对应的向量拿出来，跟P1的区别是多了个线性变换；

P3：把encoder的最后一层的所有向量取平均；

P4：把encoder的第一层与最后一层的所有向量取平均。

结果汇总 #

所有的实验结果汇总在如下三个表格中。其中表格中的每个元素是$a / b / c$的形式，代表该任务在该模型下“不加whitening”的得分为$a$、“加whitening”的得分为$b$、“加whitening并适当降维”的得分为$c$；如果$b\geq a$，那么$b$显示为绿色，否则显示为红色；如果$c\geq a$，那么$c$显示为绿色，否则显示为红色；所谓“适当降维”，对于base版本的模型是降到256维，对于large版本的模型是降到384维，对于tiny和small版则降到128维。

第一个表格是11个模型中的6个base版模型的对比，其中WoBERT和RoFormer没有NSP任务，所以没有P2的权重，测不了P2：
$$\small{\begin{array}{l|ccccc}
\hline
& \text{ATEC} & \text{BQ} & \text{LCQMC} & \text{PAWSX} & \text{STS-B} \\
\hline
\text{BERT-P1} & 16.59 / \color{green}{20.61} / \color{green}{25.58} & 29.35 / \color{red}{25.76} / \color{green}{34.66} & 41.71 / \color{green}{48.92} / \color{green}{49.18} & 15.15 / \color{green}{17.03} / \color{green}{15.98} & 34.65 / \color{green}{61.19} / \color{green}{60.07} \\
\text{BERT-P2} & 9.46 / \color{green}{22.16} / \color{green}{25.13} & 16.97 / \color{green}{18.97} / \color{green}{33.99} & 28.42 / \color{green}{49.61} / \color{green}{49.59} & 13.93 / \color{green}{16.08} / \color{green}{16.19} & 21.66 / \color{green}{60.75} / \color{green}{60.13} \\
\text{BERT-P3} & 20.79 / \color{red}{18.27} / \color{green}{28.98} & 33.08 / \color{red}{22.58} / \color{green}{38.62} & 59.22 / \color{green}{60.12} / \color{green}{62.00} & 16.68 / \color{green}{18.37} / \color{green}{17.38} & 57.48 / \color{green}{63.97} / \color{green}{68.27} \\
\text{BERT-P4} & 24.51 / \color{green}{27.00} / \color{green}{27.91} & 38.81 / \color{red}{32.29} / \color{red}{37.67} & 64.75 / \color{green}{64.75} / \color{green}{65.65} & 15.12 / \color{green}{17.80} / \color{green}{15.34} & 61.66 / \color{green}{69.45} / \color{green}{69.37} \\
\hline
\text{RoBERTa-P1} & 24.61 / \color{green}{29.59} / \color{green}{29.49} & 40.54 / \color{red}{28.95} / \color{red}{38.35} & 70.55 / \color{green}{70.82} / \color{red}{68.84} & 16.23 / \color{green}{17.99} / \color{green}{16.87} & 66.91 / \color{green}{69.19} / \color{green}{71.16} \\
\text{RoBERTa-P2} & 20.61 / \color{green}{28.91} / \color{green}{29.49} & 31.14 / \color{red}{27.48} / \color{green}{38.46} & 65.43 / \color{green}{70.62} / \color{green}{68.76} & 15.71 / \color{green}{17.30} / \color{green}{17.01} & 59.50 / \color{green}{70.77} / \color{green}{71.16} \\
\text{RoBERTa-P3} & 26.94 / \color{green}{29.94} / \color{green}{30.57} & 40.71 / \color{red}{30.95} / \color{red}{39.89} & 66.80 / \color{green}{68.00} / \color{green}{67.30} & 16.08 / \color{green}{19.01} / \color{green}{16.79} & 61.67 / \color{green}{66.19} / \color{green}{69.36} \\
\text{RoBERTa-P4} & 27.94 / \color{green}{28.33} / \color{green}{29.06} & 43.09 / \color{red}{33.49} / \color{red}{38.83} & 68.43 / \color{red}{67.86} / \color{red}{68.36} & 15.02 / \color{green}{17.91} / \color{green}{15.26} & 64.09 / \color{green}{69.74} / \color{green}{70.09} \\
\hline
\text{NEZHA-P1} & 17.39 / \color{green}{18.83} / \color{green}{24.97} & 29.63 / \color{red}{21.94} / \color{green}{33.65} & 40.60 / \color{green}{50.52} / \color{green}{46.57} & 14.90 / \color{green}{18.15} / \color{green}{16.69} & 35.84 / \color{green}{60.84} / \color{green}{58.98} \\
\text{NEZHA-P2} & 10.96 / \color{green}{23.08} / \color{green}{24.21} & 17.38 / \color{green}{28.81} / \color{green}{32.21} & 22.66 / \color{green}{49.12} / \color{green}{47.03} & 13.45 / \color{green}{18.05} / \color{green}{17.15} & 21.16 / \color{green}{60.11} / \color{green}{58.68} \\
\text{NEZHA-P3} & 23.70 / \color{red}{21.93} / \color{green}{28.65} & 35.44 / \color{red}{22.44} / \color{green}{37.95} & 60.94 / \color{green}{62.10} / \color{green}{62.50} & 18.35 / \color{green}{21.72} / \color{green}{18.78} & 60.35 / \color{green}{68.57} / \color{green}{68.97} \\
\text{NEZHA-P4} & 27.72 / \color{red}{25.31} / \color{red}{26.18} & 44.18 / \color{red}{31.47} / \color{red}{36.02} & 65.16 / \color{green}{66.68} / \color{green}{66.54} & 13.98 / \color{green}{16.66} / \color{green}{14.02} & 61.94 / \color{green}{69.55} / \color{green}{69.14} \\
\hline
\text{WoBERT-P1} & 23.88 / \color{red}{22.45} / \color{green}{27.88} & 43.08 / \color{red}{32.52} / \color{red}{37.54} & 68.56 / \color{red}{67.89} / \color{red}{65.80} & 18.15 / \color{green}{19.92} / \color{green}{18.73} & 64.12 / \color{green}{66.53} / \color{green}{69.03} \\
\text{WoBERT-P2} & \text{-} & \text{-} & \text{-} & \text{-} & \text{-} \\
\text{WoBERT-P3} & 24.62 / \color{red}{22.74} / \color{green}{29.01} & 40.64 / \color{red}{28.12} / \color{red}{38.82} & 64.89 / \color{green}{65.22} / \color{green}{65.14} & 16.83 / \color{green}{20.56} / \color{green}{17.87} & 59.43 / \color{green}{66.57} / \color{green}{67.76} \\
\text{WoBERT-P4} & 25.97 / \color{green}{27.24} / \color{green}{28.38} & 42.37 / \color{red}{32.34} / \color{red}{38.06} & 66.53 / \color{red}{65.62} / \color{red}{66.36} & 15.54 / \color{green}{18.85} / \color{green}{15.98} & 61.37 / \color{green}{68.11} / \color{green}{68.42} \\
\hline
\text{RoFormer-P1} & 24.29 / \color{green}{26.04} / \color{green}{28.20} & 41.91 / \color{red}{28.13} / \color{red}{38.21} & 64.87 / \color{red}{60.92} / \color{red}{60.83} & 20.15 / \color{green}{23.08} / \color{green}{21.30} & 59.91 / \color{green}{66.96} / \color{green}{66.86} \\
\text{RoFormer-P2} & \text{-} & \text{-} & \text{-} & \text{-} & \text{-} \\
\text{RoFormer-P3} & 24.09 / \color{green}{28.51} / \color{green}{29.37} & 39.09 / \color{red}{34.92} / \color{red}{39.05} & 63.55 / \color{green}{63.85} / \color{green}{63.58} & 16.53 / \color{green}{18.43} / \color{green}{17.52} & 58.98 / \color{red}{55.30} / \color{green}{67.32} \\
\text{RoFormer-P4} & 25.92 / \color{green}{27.38} / \color{green}{28.37} & 41.75 / \color{red}{32.36} / \color{red}{38.05} & 66.18 / \color{red}{65.45} / \color{red}{65.63} & 15.30 / \color{green}{18.36} / \color{green}{15.69} & 61.40 / \color{green}{68.02} / \color{green}{68.27} \\
\hline
\text{SimBERT-P1} & 38.50 / \color{red}{23.64} / \color{red}{30.79} & 48.54 / \color{red}{31.78} / \color{red}{40.01} & 76.23 / \color{red}{75.05} / \color{red}{74.50} & 15.10 / \color{green}{18.49} / \color{green}{15.64} & 74.14 / \color{red}{73.37} / \color{green}{75.29} \\
\text{SimBERT-P2} & 38.93 / \color{red}{27.06} / \color{red}{30.79} & 49.93 / \color{red}{35.38} / \color{red}{40.14} & 75.56 / \color{red}{73.45} / \color{red}{74.39} & 14.52 / \color{green}{18.51} / \color{green}{15.74} & 73.18 / \color{green}{73.43} / \color{green}{75.12} \\
\text{SimBERT-P3} & 36.50 / \color{red}{31.32} / \color{red}{31.24} & 45.78 / \color{red}{29.17} / \color{red}{40.98} & 74.42 / \color{red}{73.79} / \color{red}{73.43} & 15.33 / \color{green}{18.39} / \color{green}{15.87} & 67.31 / \color{green}{70.70} / \color{green}{72.00} \\
\text{SimBERT-P4} & 33.53 / \color{red}{29.04} / \color{red}{28.78} & 45.28 / \color{red}{34.70} / \color{red}{39.00} & 73.20 / \color{red}{71.22} / \color{red}{72.09} & 14.16 / \color{green}{17.32} / \color{green}{14.39} & 66.98 / \color{green}{70.55} / \color{green}{71.43} \\
\hline
\end{array}}$$

第二个表格则是3个large版模型的对比：
$$\small{\begin{array}{l|ccccc}
\hline
& \text{ATEC} & \text{BQ} & \text{LCQMC} & \text{PAWSX} & \text{STS-B} \\
\hline
\text{BERT}_{\text{large}}\text{-P1} & 13.15 / \color{green}{22.42} / \color{green}{24.32} & 19.81 / \color{red}{17.61} / \color{green}{31.09} & 23.45 / \color{green}{44.31} / \color{green}{41.32} & 16.88 / \color{green}{19.37} / \color{green}{19.87} & 25.93 / \color{green}{52.70} / \color{green}{56.74} \\
\text{BERT}_{\text{large}}\text{-P2} & 8.16 / \color{green}{16.57} / \color{green}{24.34} & 9.43 / \color{green}{18.23} / \color{green}{30.91} & 16.66 / \color{green}{39.50} / \color{green}{41.40} & 14.72 / \color{green}{20.00} / \color{green}{19.92} & 15.82 / \color{green}{56.79} / \color{green}{56.73} \\
\text{BERT}_{\text{large}}\text{-P3} & 24.31 / \color{red}{18.25} / \color{green}{30.24} & 35.87 / \color{red}{32.56} / \color{green}{37.51} & 59.29 / \color{green}{65.06} / \color{green}{63.78} & 16.94 / \color{green}{20.01} / \color{green}{18.62} & 60.22 / \color{green}{68.07} / \color{green}{68.87} \\
\text{BERT}_{\text{large}}\text{-P4} & 25.62 / \color{green}{27.64} / \color{green}{28.15} & 38.45 / \color{red}{31.30} / \color{red}{36.47} & 65.43 / \color{green}{66.54} / \color{green}{67.02} & 15.33 / \color{green}{19.06} / \color{green}{15.95} & 62.02 / \color{green}{69.74} / \color{green}{69.99} \\
\hline
\text{RoBERTa}_{\text{large}}\text{-P1} & 19.32 / \color{red}{15.90} / \color{green}{29.32} & 34.21 / \color{red}{23.16} / \color{green}{37.11} & 64.89 / \color{green}{67.05} / \color{green}{66.49} & 17.78 / \color{green}{20.66} / \color{green}{19.73} & 60.16 / \color{green}{69.46} / \color{green}{70.44} \\
\text{RoBERTa}_{\text{large}}\text{-P2} & 19.32 / \color{green}{22.16} / \color{green}{29.23} & 34.33 / \color{red}{33.22} / \color{green}{37.10} & 65.00 / \color{green}{67.12} / \color{green}{66.50} & 17.77 / \color{green}{18.90} / \color{green}{19.79} & 60.09 / \color{green}{61.35} / \color{green}{70.32} \\
\text{RoBERTa}_{\text{large}}\text{-P3} & 24.83 / \color{red}{21.05} / \color{green}{30.85} & 39.23 / \color{red}{26.85} / \color{red}{38.39} & 66.86 / \color{green}{68.62} / \color{green}{67.25} & 17.67 / \color{green}{20.06} / \color{green}{19.09} & 62.98 / \color{red}{55.75} / \color{green}{69.72} \\
\text{RoBERTa}_{\text{large}}\text{-P4} & 25.69 / \color{green}{28.19} / \color{green}{28.39} & 40.18 / \color{red}{32.06} / \color{red}{36.91} & 68.58 / \color{green}{68.74} / \color{green}{68.71} & 16.01 / \color{green}{19.87} / \color{green}{16.50} & 63.75 / \color{green}{70.08} / \color{green}{70.39} \\
\hline
\text{NEZHA}_{\text{large}}\text{-P1} & 18.91 / \color{green}{24.98} / \color{green}{25.68} & 30.39 / \color{red}{29.30} / \color{green}{33.29} & 41.68 / \color{green}{52.42} / \color{green}{49.80} & 18.89 / \color{green}{23.31} / \color{green}{21.74} & 39.04 / \color{green}{60.36} / \color{green}{61.13} \\
\text{NEZHA}_{\text{large}}\text{-P2} & 7.92 / \color{green}{21.60} / \color{green}{25.33} & 12.03 / \color{green}{24.63} / \color{green}{33.22} & 12.33 / \color{green}{52.40} / \color{green}{49.68} & 16.26 / \color{green}{23.11} / \color{green}{21.95} & 16.59 / \color{green}{57.70} / \color{green}{60.82} \\
\text{NEZHA}_{\text{large}}\text{-P3} & 22.74 / \color{green}{25.63} / \color{green}{27.48} & 36.48 / \color{red}{22.33} / \color{red}{35.47} & 59.65 / \color{green}{59.90} / \color{green}{59.94} & 18.09 / \color{green}{23.12} / \color{green}{19.71} & 59.66 / \color{green}{67.80} / \color{green}{68.55} \\
\text{NEZHA}_{\text{large}}\text{-P4} & 27.45 / \color{red}{24.83} / \color{red}{24.90} & 44.33 / \color{red}{29.73} / \color{red}{34.05} & 66.19 / \color{green}{66.89} / \color{green}{67.88} & 13.74 / \color{green}{16.66} / \color{green}{13.95} & 62.91 / \color{green}{69.87} / \color{green}{69.71} \\
\hline
\end{array}}$$

第三个表格则是不同大小的SimBERT模型之间的对比：
$$\small{\begin{array}{l|ccccc}
\hline
& \text{ATEC} & \text{BQ} & \text{LCQMC} & \text{PAWSX} & \text{STS-B} \\
\hline
\text{SimBERT}\text{-P1} & 38.50 / \color{red}{23.64} / \color{red}{30.79} & 48.54 / \color{red}{31.78} / \color{red}{40.01} & 76.23 / \color{red}{75.05} / \color{red}{74.50} & 15.10 / \color{green}{18.49} / \color{green}{15.64} & 74.14 / \color{red}{73.37} / \color{green}{75.29} \\
\text{SimBERT}\text{-P2} & 38.93 / \color{red}{27.06} / \color{red}{30.79} & 49.93 / \color{red}{35.38} / \color{red}{40.14} & 75.56 / \color{red}{73.45} / \color{red}{74.39} & 14.52 / \color{green}{18.51} / \color{green}{15.74} & 73.18 / \color{green}{73.43} / \color{green}{75.12} \\
\text{SimBERT}\text{-P3} & 36.50 / \color{red}{31.32} / \color{red}{31.24} & 45.78 / \color{red}{29.17} / \color{red}{40.98} & 74.42 / \color{red}{73.79} / \color{red}{73.43} & 15.33 / \color{green}{18.39} / \color{green}{15.87} & 67.31 / \color{green}{70.70} / \color{green}{72.00} \\
\text{SimBERT}\text{-P4} & 33.53 / \color{red}{29.04} / \color{red}{28.78} & 45.28 / \color{red}{34.70} / \color{red}{39.00} & 73.20 / \color{red}{71.22} / \color{red}{72.09} & 14.16 / \color{green}{17.32} / \color{green}{14.39} & 66.98 / \color{green}{70.55} / \color{green}{71.43} \\
\hline
\text{SimBERT}_{\text{small}}\text{-P1} & 30.68 / \color{red}{27.56} / \color{red}{29.07} & 43.41 / \color{red}{30.89} / \color{red}{39.78} & 74.73 / \color{red}{73.21} / \color{red}{73.50} & 15.89 / \color{green}{17.96} / \color{green}{16.75} & 70.54 / \color{green}{71.39} / \color{green}{72.14} \\
\text{SimBERT}_{\text{small}}\text{-P2} & 31.00 / \color{red}{29.14} / \color{red}{29.11} & 43.76 / \color{red}{36.86} / \color{red}{39.84} & 74.21 / \color{red}{73.14} / \color{red}{73.67} & 16.17 / \color{green}{18.12} / \color{green}{16.81} & 70.10 / \color{green}{71.40} / \color{green}{72.28} \\
\text{SimBERT}_{\text{small}}\text{-P3} & 30.03 / \color{red}{21.24} / \color{red}{29.30} & 43.72 / \color{red}{31.69} / \color{red}{40.81} & 72.12 / \color{red}{70.27} / \color{red}{70.52} & 16.93 / \color{green}{21.68} / \color{green}{18.75} & 66.55 / \color{red}{66.11} / \color{green}{69.19} \\
\text{SimBERT}_{\text{small}}\text{-P4} & 29.52 / \color{red}{28.41} / \color{red}{28.57} & 43.52 / \color{red}{36.56} / \color{red}{40.49} & 70.33 / \color{red}{68.75} / \color{red}{69.01} & 15.39 / \color{green}{21.57} / \color{green}{16.34} & 64.73 / \color{green}{68.12} / \color{green}{68.24} \\
\hline
\text{SimBERT}_{\text{tiny}}\text{-P1} & 30.51 / \color{red}{24.67} / \color{red}{27.98} & 44.25 / \color{red}{31.75} / \color{red}{39.42} & 74.27 / \color{red}{72.25} / \color{red}{73.24} & 16.01 / \color{green}{18.07} / \color{green}{17.07} & 70.11 / \color{red}{66.39} / \color{green}{71.92} \\
\text{SimBERT}_{\text{tiny}}\text{-P2} & 30.01 / \color{red}{27.66} / \color{red}{27.92} & 44.47 / \color{red}{37.33} / \color{red}{39.39} & 73.98 / \color{red}{72.31} / \color{red}{73.31} & 16.55 / \color{green}{18.15} / \color{green}{17.14} & 70.35 / \color{green}{70.88} / \color{green}{72.04} \\
\text{SimBERT}_{\text{tiny}}\text{-P3} & 28.47 / \color{red}{19.68} / \color{green}{28.60} & 42.04 / \color{red}{29.49} / \color{red}{40.59} & 69.16 / \color{red}{66.99} / \color{red}{67.74} & 16.18 / \color{green}{20.11} / \color{green}{17.87} & 64.41 / \color{green}{66.72} / \color{green}{67.57} \\
\text{SimBERT}_{\text{tiny}}\text{-P4} & 27.77 / \color{red}{27.67} / \color{green}{28.02} & 41.76 / \color{red}{37.02} / \color{red}{40.19} & 67.55 / \color{red}{65.66} / \color{red}{66.60} & 15.06 / \color{green}{20.49} / \color{green}{16.26} & 62.92 / \color{green}{66.77} / \color{green}{67.01} \\
\hline
\end{array}}$$

实验结论 #

跟英文任务的表格类似，绿色意味着whitening操作提升了句向量质量，红色则意味着whitening降低了句向量质量，绿色越多则意味着whitening方法越有效。从上述几个表格中，我们可以得出一些结论：

1、中文任务的测试结果比英文任务复杂得多，更加不规律，比如在英文任务中，P4这种Pooling方式基本上都比其他方式好，而large模型基本上比base好，但这些情况在中文任务中都不明显；

2、除了SimBERT外，整体而言还是绿色比红色多，所以whitening对句向量的改善基本上还是有正面作用的，特别地，在$a / b / c$中，$c$的绿色明显比$b$的绿色要多，这说明降维还能进一步提升效果，也就是说whitening是真正的提速又提效的算法；

3、在BQ任务中，whitening方法几乎都带来了下降，这跟英文任务中的SICK-R任务类似，这说明“天下没有免费的午餐”，总有一些任务会使得“各向同性”假设失效，这时候不管是BERT-whitening还是BERT-flow都不能带来提升；

4、SimBERT是所有除PAWSX外的任务的SOTA，当然SimBERT算是经过语义相似度任务有监督训练过的了（但理论上训练数据与测试任务没有交集），所以跟其他模型比肯定不是特别公平的，但不管怎样，SimBERT已经开源，大家都可以用，所以可以作为一个baseline对待；

5、SimBERT加whitening，要不会带来性能下降，要不就是有提升也不明显，这说明如果通过有监督方法训练出来的句向量，就没有必要进一步做whitening了，基本上不会带来提升；

6、PAWSX确实很难，语义相似度任务还任重道远...

本文小结 #

本文介绍了我们在中英文任务上对无监督语义相似度方法的比较全面评测。在英文任务方面，主要复述了我们的BERT-whitening方法的论文中的结果，里边包含了跟BERT-flow一一对齐的比较；在中文方面，我们收集了5个任务，在11个预训练模型、4种Pooling方式、3种后处理方式共600多种组合进行了评测，以提供一个可以方便大家对比的结果。

一句话总结评测结果，那就是：BERT-whitening方法确实达到了当前无监督语义的SOTA，而SimBERT则是中文语义相似度的一个比较高的开源baseline。

转载到请包括本文地址：https://kexue.fm/archives/8321

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (Apr. 11, 2021). 《无监督语义相似度哪家强？我们做了个比较全面的评测 》[Blog post]. Retrieved from https://kexue.fm/archives/8321

@online{kexuefm-8321,
        title={无监督语义相似度哪家强？我们做了个比较全面的评测},
        author={苏剑林},
        year={2021},
        month={Apr},
        url={\url{https://kexue.fm/archives/8321}},
}