从动力学角度看优化算法(六):为什么SimSiam不退化?
By 苏剑林 | 2020-12-11 | 91872位读者 |自SimCLR以来,CV中关于无监督特征学习的工作层出不穷,让人眼花缭乱。这些工作大多数都是基于对比学习的,即通过适当的方式构造正负样本进行分类学习的。然而,在众多类似的工作中总有一些特立独行的研究,比如Google的BYOL和最近的SimSiam,它们提出了单靠正样本就可以完成特征学习的方案,让人觉得耳目一新。但是没有负样本的支撑,模型怎么不会退化(坍缩)为一个没有意义的常数模型呢?这便是这两篇论文最值得让人思考和回味的问题了。
其中SimSiam给出了让很多人都点赞的答案,但笔者觉得SimSiam也只是把问题换了种说法,并没有真的解决这个问题。笔者认为,像SimSiam、GAN等模型的成功,很重要的原因是使用了基于梯度的优化器(而非其他更强或者更弱的优化器),所以不结合优化动力学的答案都是不完整的。在这里,笔者尝试结合动力学来分析SimSiam不会退化的原因。
SimSiam #
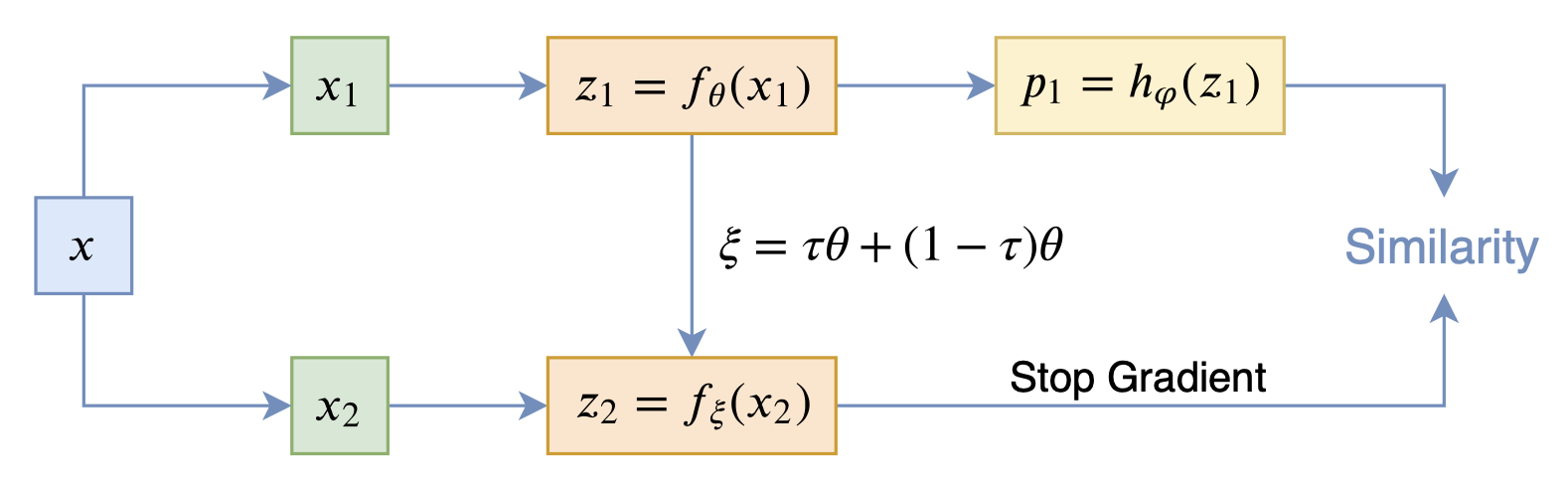
在看SimSiam之前,我们可以先看看BYOL,来自论文《Bootstrap your own latent: A new approach to self-supervised Learning》,其学习过程很简单,就是维护两个编码器Student和Teacher,其中Teacher是Student的滑动平均,Student则又反过来向Teacher学习,有种“左脚踩右脚”就可以飞起来的感觉。示意图如下:
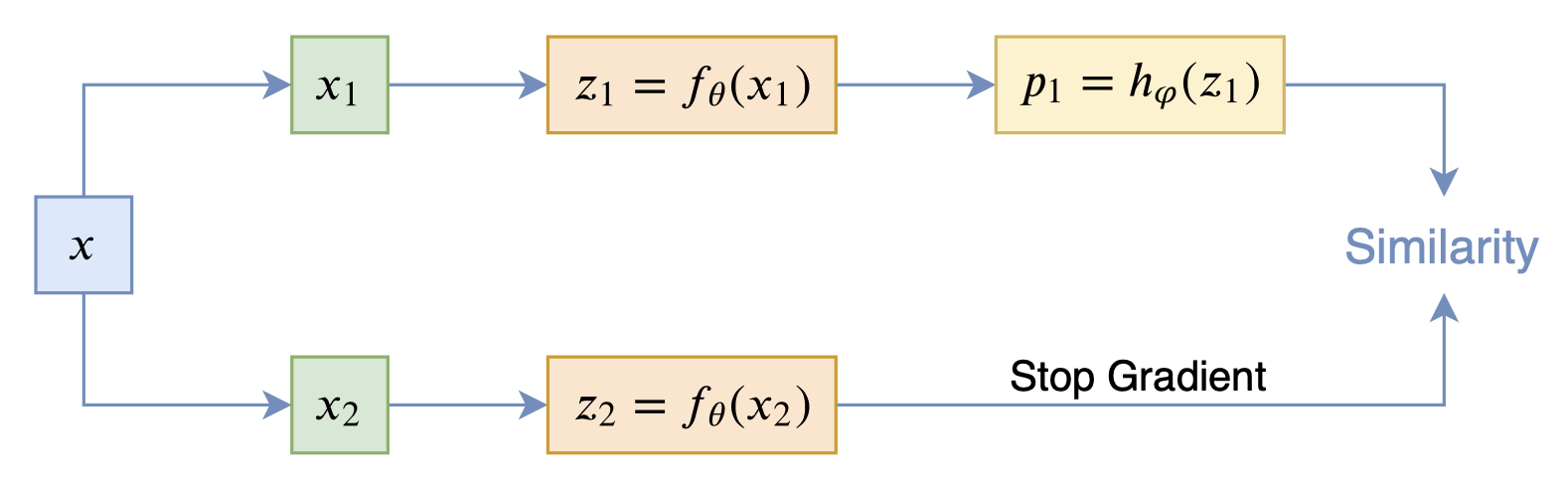
而SimSiam则来自论文《Exploring Simple Siamese Representation Learning》,它更加简单,直接把BYOL的滑动平均去掉了:
事实上,SimSiam相当于将BYOL的滑动平均参数$\tau$设置为0了,这说明BYOL的滑动平均不是必须的。为了找出算法中的关键部分,SimSiam还做了很多对比实验,证实了stop_gradient算子以及predictor模块$h_{\varphi}(z)$是SimSiam不退化的关键。为了解释这个现象,SimSiam提出了该优化过程实际上相当于在交替优化
\begin{equation}\mathcal{L}(\theta, \eta)=\mathbb{E}_{x, \mathcal{T}}\left[\left\Vert\mathcal{F}_{\theta}(\mathcal{T}(x))-\eta_{x}\right\Vert^2\right]\label{eq:simsiam}\end{equation}
其中$x$代表训练样本而$\mathcal{T}$代表数据扩增。这部分内容网上已有不少解读,直接读原论文也不困难,因此就不详细展开了。
动力学分析 #
然而,笔者认为,将SimSiam算法的理解转换成$\mathcal{L}(\theta, \eta)$的交替优化的理解,只不过是换了种说法,并没有作出什么实质的回答。因为很明显,目前$\mathcal{L}(\theta, \eta)$也存在退化解,模型完全可以让所有的$\eta_{x}$都等于同一个向量,然后$\mathcal{F}_{\theta}$输出同一个常数向量。不回答$\mathcal{L}(\theta, \eta)$的交替优化为什么不退化,那也等于没有回答问题。
下面笔者将列举出自认为是SimSiam不退化的关键因素,并且通过一个简单的例子表明回答不退化的原因需要跟动力学结合起来。当然,笔者这部分的论述其实也是不完整的,甚至是不严谨的,只是抛砖引玉地给出一个新的视角。
深度图像先验 #
首先,很早之前人们就发现一个随机初始化的CNN模型就可以直接用来提取视觉特征,效果也不会特别差,该结论可以追溯到2009年的论文《What is the best multi-stage architecture for object recognition?》,这可以理解为CNN天然具有处理图像的能力。后来这个特性被起了一个高大上的名字,称为“深度图像先验”,出自论文《Deep Image Prior》,里边做了一些实验,表明从一个随机初始化的CNN模型出发,不需要任何监督学习,就可以完成图像补全、去噪等任务,进一步确认了CNN天然具有处理图像的能力这个特性。
按照笔者的理解,“深度图像先验”源于三点:
1、图像的连续性,是指图像本身就可以直接视为一个连续型向量,而不需要像NLP那样要学习出Embedding层出来,这意味着我们用“原始图像+K邻近”这样简单粗暴的方法就可以做很多任务了;
2、CNN的架构先验,指的是CNN的局部感知设计确实很好地模拟了肉眼的视觉处理过程,而我们所给出的视觉分类结果也都是基于我们的肉眼所下的结论,因此两者是契合的;
3、良好的初始化,这不难理解,再好的模型配上全零初始化了估计都不会work,之前的文章《从几何视角来理解模型参数的初始化策略》也简单讨论过初始化方法,从几何意义上来看,主流的初始化方法都是一种近似的“正交变换”,能尽量地保留输入特征的信息。
不退化的动力学 #
还是那句话,深度图像先验意味着一个随机化的CNN模型就是一个不是特别差的编码器了,于是我们接下来要做的事情无非可以归结为两点:往更好地方向学、不要向常数退化。
往更好地方向学,就是通过人为地设计一些先验信号,让模型更好地融入这些先验知识。SimSiam、BYOL等让同一张图片做两种不同的数据扩增,然后两者对应的特征向量尽量地相似,这便是一种好的信号引导,告诉模型简单的变换不应当影响我们对视觉理解,事实上,这也是所有对比学习方法所用的设计之一。
不同的则是在“不要向常数退化”这一点上,一般的对比学习方法是通过构造负样本来告诉模型哪些图片的特征不该相近,从而让模型不退化;但是SimSiam、BYOL不一样,它们没有负样本,实际上它们是通过将模型的优化过程分解为两个同步的、但是快慢不一样的模块来防止退化的。还是以SimSiam为例,它的优化目标可以写为
\begin{equation}\mathcal{L}(\varphi, \theta)=\mathbb{E}_{x, \mathcal{T}_1,\mathcal{T}_2}\Big[l\left(h_{\varphi}(f_{\theta}(\mathcal{T}_1(x))), f_{\theta}(\mathcal{T}_2(x))\right)\Big]\end{equation}
然后用梯度下降来优化,对应的动力学方程组是
\begin{equation}\begin{aligned}
\frac{d\varphi}{dt} = - \frac{\partial\mathcal{L}}{\partial \varphi} =& -\mathbb{E}_{x, \mathcal{T}_1,\mathcal{T}_2}\bigg[\frac{\partial l}{\partial h}\frac{\partial h}{\partial \varphi}\bigg]\\
\frac{d\theta}{dt} = - \frac{\partial\mathcal{L}}{\partial \theta} =& -\mathbb{E}_{x, \mathcal{T}_1,\mathcal{T}_2}\bigg[\frac{\partial l}{\partial h}\frac{\partial h}{\partial f}\frac{\partial f}{\partial \theta} \color{skyblue}{\,+\underbrace{\frac{\partial l}{\partial f}\frac{\partial f}{\partial \theta}}_{\begin{aligned}\text{SimSiam}\\\text{去掉了它}\end{aligned}}}\bigg]
\end{aligned}\end{equation}
上式已经注明了有无stop_gradient算子所带来的差别。简单来说,如果添加了stop_gradient算子,那么$\frac{d\theta}{dt}$就少了第二项,这时候$\frac{d\varphi}{dt}$和$\frac{d\theta}{dt}$都共同包含因子$\frac{\partial l}{\partial h}$,由于$h_{\varphi}$更靠近输出层,并且初始化的$f_{\theta}$也是一个不差的编码器,因此开始学习的时候,$h_{\varphi}$会被优化得更快,越靠近输入层的优化得越慢。也就是说,$\frac{d\varphi}{dt}$是快动力学部分,$\frac{d\theta}{dt}$则是慢动力学部分,那么相对而言,$\frac{d\varphi}{dt}$会更快速地收敛到0,这意味着$\frac{\partial l}{\partial h}$会很快地变得很小,由于$\frac{d\theta}{dt}$也包含$\frac{\partial l}{\partial h}$这一项,所以$\frac{d\theta}{dt}$跟着变得小,在它退化之前,推动它退化的力都已经微乎其微了,也就不会退化了。相反,如果有第二项$\frac{\partial l}{\partial f}\frac{\partial f}{\partial \theta}$(不管是补充上它还是只保留它),那么就相当于添加了一个“快速通道”,使得它变为快速项,就算$\frac{\partial l}{\partial h}=0$,但由于第二项在,还会继续推动着它退化。
举个简单的具体例子,我们考虑
\begin{equation}l = \frac{1}{2}(\varphi\theta - \theta)^2\end{equation}
简单起见这里的$\varphi,\theta$都是标量,对应动力学方程是
\begin{equation}\frac{d\varphi}{dt}=-(\varphi\theta - \theta)\theta, \quad\frac{d\theta}{dt}=-(\varphi\theta - \theta) \varphi \color{skyblue}{+ \underbrace{(\varphi\theta - \theta)}_{\begin{aligned}\text{SimSiam}\theta\\ \text{去掉了它}\end{aligned}}}\end{equation}
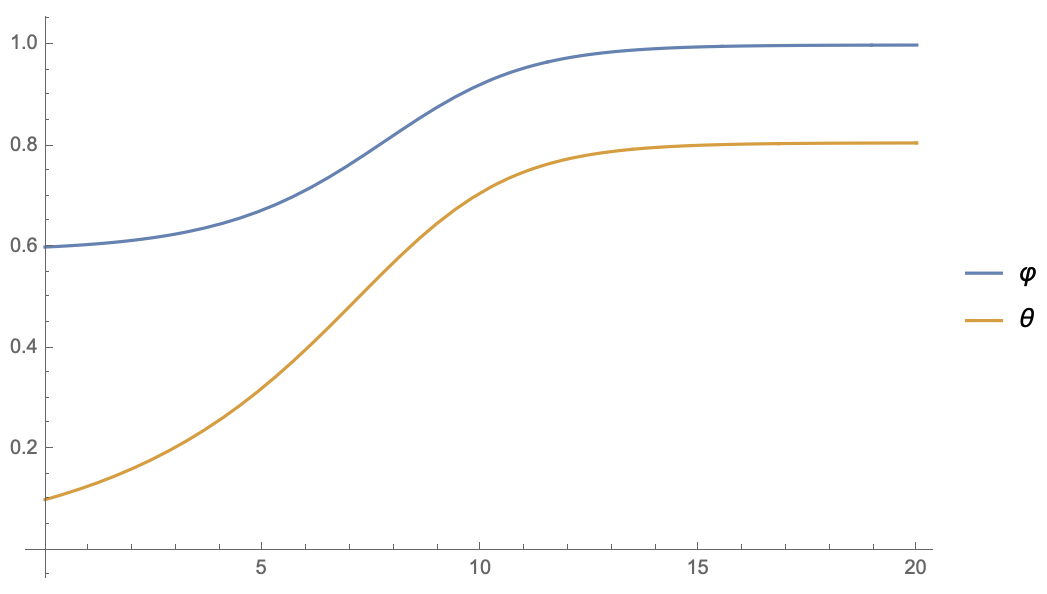
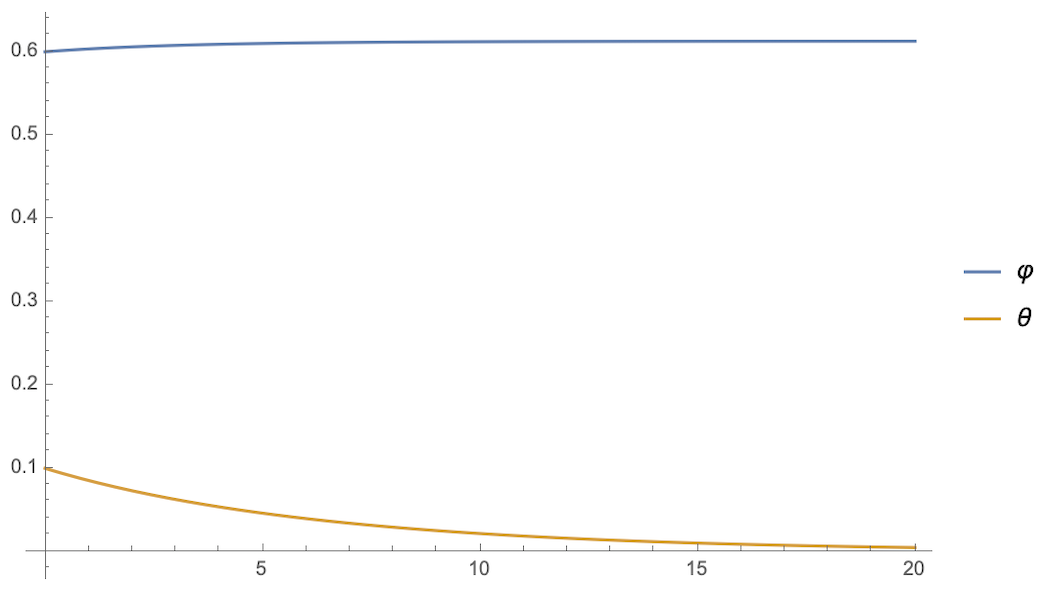
假设$\varphi(0)=0.6, \theta(0)=0.1$(随便选的),那么两者的演变是:
可以看到,停掉第二个$\theta$的梯度后,$\varphi$和$\theta$的方程是相当一致的,$\varphi$迅速趋于1,同时$\theta$稳定到了一个非0值(意味着没退化)。相当,如果补充上$\frac{d\theta}{dt}$的第二项,或者干脆只保留第二项,结果都是$\theta$迅速趋于0,而$\varphi$则无法趋于1了,这意味着主导权被$\theta$占据了。
这个例子本身没多大说服力,但是它简单地揭示了动力学的变化情况:
predictor($\varphi$)的引入使得模型的动力学分为了两大部分,stop_gradient算子的引入则使得encoder部分($\theta$)的动力学变慢,并且增强了encoder与predictor的同步性,这样一来,predictor以“迅雷不及掩耳之势”拟合了目标,使得encoder还没来得及退化,优化过程就停止了。
看近似展开 #
当然,诠释千万种,皆是“马后炮”,真正牛的还是发现者,我们充其量也就是蹭掉热度而已。这里再多蹭一下,分享笔者从另外一个视角看的SimSiam。文章开头说了,SimSiam论文提出了通过目标$\eqref{eq:simsiam}$的交替优化来解释SimSiam,这个视角就是从目标$\eqref{eq:simsiam}$出发,进一步深究一下它不退化的原因。
如果固定$\theta$,那么对于目标$\eqref{eq:simsiam}$来说,很容易解出$\eta_x$的最优值为
\begin{equation}\eta_x=\mathbb{E}_{\mathcal{T}}\left[\mathcal{F}_{\theta}(\mathcal{T}(x))\right]\end{equation}
代入$\eqref{eq:simsiam}$,就得到优化目标为
\begin{equation}\mathcal{L}(\theta)=\mathbb{E}_{x, \mathcal{T}}\bigg[\Big\Vert\mathcal{F}_{\theta}(\mathcal{T}(x))-\mathbb{E}_{\mathcal{T}}\left[\mathcal{F}_{\theta}(\mathcal{T}(x))\right]\Big\Vert^2\bigg]\end{equation}
我们假定$\mathcal{T}(x)-x$是“小”的向量,那么在$x$处做一阶展开得到
\begin{equation}\mathcal{L}(\theta)\approx\mathbb{E}_{x, \mathcal{T}}\bigg[\left\Vert\frac{\partial \mathcal{F}_{\theta}(x)}{\partial x}\big(\mathcal{T}(x)-\bar{x}\big)\right\Vert^2\bigg]\label{eq:em-sim}\end{equation}
其中$\bar{x}=\mathbb{E}_{\mathcal{T}}\left[\mathcal{T}(x)\right]$是同一张图片在所有数据扩增手段下的平均结果,注意它通常不等于$x$。类似地,如果是不加stop_gradient也不加predictor的SimSiam,那么损失函数近似为
\begin{equation}\mathcal{L}(\theta)\approx\mathbb{E}_{x, \mathcal{T}_1, \mathcal{T}_2}\bigg[\left\Vert\frac{\partial \mathcal{F}_{\theta}(x)}{\partial x}\big(\mathcal{T}_2(x)-\mathcal{T}_1(x)\big)\right\Vert^2\bigg]\label{eq:em-sim-2}\end{equation}
在式$\eqref{eq:em-sim}$中,每个$\mathcal{T}(x)$减去了$\bar{x}$,可以证明这个选择能使得损失函数最小;而在式$\eqref{eq:em-sim-2}$中,每个$\mathcal{T}_1(x)$减去的是另一个扩增结果$\mathcal{T}_2(x)$,会导致损失函数本身和估计的方差都大大增大。
那是不是意味着,不加stop_gradient、不加predictor会失败的原因,是因为它的损失函数以及方差过大呢?注意到在一阶近似下有$\eta_x\approx \mathcal{F}_{\theta}(\bar{x})$,那如果优化目标换成
\begin{equation}\mathcal{L}(\theta)=\mathbb{E}_{x, \mathcal{T}}\bigg[\Big\Vert\mathcal{F}_{\theta}(\mathcal{T}(x))-\mathcal{F}_{\theta}(\bar{x})\Big\Vert^2\bigg]\end{equation}
是不是就不会退化了?笔者也没有验证过,不得而知,正在研究相关内容的读者不妨验证一下。这里还引申出一个相关的问题,经过这样训练好的编码器,究竟用$\mathcal{F}_{\theta}(x)$还是$\mathcal{F}_{\theta}(\bar{x})$作为特征好呢?
当然,这部分的讨论都是建立在“$\mathcal{T}(x)-x$是小的向量”这个假设的基础上的,如果它不成立,那么这一节内容就是白说了。
下文末小结 #
本文试图从动力学角度给出笔者对BYOL、SimSiam算法不退化的理解,很遗憾,写到一半的时候发现之前头脑中构思的一些分析无法自圆其说了,于是删减了一些内容,并补充了一个新的角度,尽量让文章不“烂尾”,至于求精,那是说不上了。权当笔记分享在此,如有不当之处,还望读者海涵斧正。
转载到请包括本文地址:https://kexue.fm/archives/7980
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Dec. 11, 2020). 《从动力学角度看优化算法(六):为什么SimSiam不退化? 》[Blog post]. Retrieved from https://kexue.fm/archives/7980
@online{kexuefm-7980,
title={从动力学角度看优化算法(六):为什么SimSiam不退化?},
author={苏剑林},
year={2020},
month={Dec},
url={\url{https://kexue.fm/archives/7980}},
}










March 4th, 2022
苏神,如果另一个分支也有predictor,并且分支也做梯度停止, 和这种不对称的相比,参数优化有什么区别吗