也来谈谈RNN的梯度消失/爆炸问题

尽管Transformer类的模型已经攻占了NLP的多数领域，但诸如LSTM、GRU之类的RNN模型依然在某些场景下有它的独特价值，所以RNN依然是值得我们好好学习的模型。而对于RNN梯度的相关分析，则是一个从优化角度思考分析模型的优秀例子，值得大家仔细琢磨理解。君不见，诸如“LSTM为什么能解决梯度消失/爆炸”等问题依然是目前流行的面试题之一...

经典的LSTM

关于此类问题，已有不少网友做出过回答，然而笔者查找了一些文章（包括知乎上的部分回答、专栏以及经典的英文博客），发现没有找到比较好的答案：有些推导记号本身就混乱不堪，有些论述过程没有突出重点，整体而言感觉不够清晰自洽。为此，笔者也尝试给出自己的理解，供大家参考。

RNN及其梯度 #

RNN的统一定义为
\begin{equation}h_t = f\left(x_t, h_{t-1};\theta\right)\end{equation}
其中$h_t$是每一步的输出，它由当前输入$x_t$和前一时刻输出$h_{t-1}$共同决定，而$\theta$则是可训练参数。在做最基本的分析时，我们可以假设$h_t,x_t,\theta$都是一维的，这可以让我们获得最直观的理解，并且其结果对高维情形仍有参考价值。之所以要考虑梯度，是因为我们目前主流的优化器还是梯度下降及其变种，因此要求我们定义的模型有一个比较合理的梯度。我们可以求得：
\begin{equation}\frac{d h_t}{d\theta} = \frac{\partial h_t}{\partial h_{t-1}}\frac{d h_{t-1}}{d\theta} + \frac{\partial h_t}{\partial \theta}\end{equation}
可以看到，其实RNN的梯度也是一个RNN，当前时刻梯度$\frac{d h_t}{d\theta}$是前一时刻梯度$\frac{d h_{t-1}}{d\theta}$与当前运算梯度$\frac{\partial h_t}{\partial \theta}$的函数。同时，从上式我们就可以看出，其实梯度消失或者梯度爆炸现象几乎是必然存在的：当$\left|\frac{\partial h_t}{\partial h_{t-1}}\right| < 1$时，意味着历史的梯度信息是衰减的，因此步数多了梯度必然消失（好比$\lim\limits_{n\to\infty} 0.9^n \to 0$）；当$\left|\frac{\partial h_t}{\partial h_{t-1}}\right| > 1$，因为这历史的梯度信息逐步增强，因此步数多了梯度必然爆炸（好比$\lim\limits_{n\to\infty} 1.1^n \to \infty$）。总不可能一直$\left|\frac{\partial h_t}{\partial h_{t-1}}\right| = 1$吧？当然，也有可能有些时刻大于1，有些时刻小于1，最终稳定在1附近，但这样概率很小，需要很精巧地设计模型才行。

所以步数多了，梯度消失或爆炸几乎都是不可避免的，我们只能对于有限的步数去缓解这个问题。

消失还是爆炸？ #

说到这里，我们还没说清楚一个问题：什么是RNN的梯度消失/爆炸？梯度爆炸好理解，就是梯度数值发散，甚至慢慢就NaN了；那梯度消失就是梯度变成零吗？并不是，我们刚刚说梯度消失是$\left|\frac{\partial h_t}{\partial h_{t-1}}\right|$一直小于1，历史梯度不断衰减，但不意味着总的梯度就为0了，具体来说，一直迭代下去，我们有
\begin{equation}\begin{aligned}\frac{d h_t}{d\theta} =& \frac{\partial h_t}{\partial h_{t-1}}\frac{d h_{t-1}}{d\theta} + \frac{\partial h_t}{\partial \theta}\\
=& \frac{\partial h_t}{\partial \theta}+\frac{\partial h_t}{\partial h_{t-1}}\frac{\partial h_{t-1}}{\partial \theta}+\frac{\partial h_t}{\partial h_{t-1}}\frac{\partial h_{t-1}}{\partial h_{t-2}}\frac{\partial h_{t-2}}{\partial \theta}+\dots\\
\end{aligned}\end{equation}
显然，其实只要$\frac{\partial h_t}{\partial \theta}$不为0，那么总梯度为0的概率其实是很小的；但是一直迭代下去的话，那么$\frac{\partial h_1}{\partial \theta}$这一项前面的稀疏就是$t-1$项的连乘$\frac{\partial h_t}{\partial h_{t-1}}\frac{\partial h_{t-1}}{\partial h_{t-2}}\cdots\frac{\partial h_2}{\partial h_1}$，如果它们的绝对值都小于1，那么结果就会趋于0，这样一来，$\frac{d h_t}{d\theta}$几乎就没有包含最初的梯度$\frac{\partial h_1}{\partial \theta}$的信息了，这才是RNN中梯度消失的含义：距离当前时间步越长，那么其反馈的梯度信号越不显著，最后可能完全没有起作用，这就意味着RNN对长距离语义的捕捉能力失效了。

说白了，你优化过程都跟长距离的反馈没关系，怎么能保证学习出来的模型能有效捕捉长距离呢？

几个数学公式 #

上面的文字都是一般性的分析，接下来我们具体RNN具体分析。不过在此之前，我们需要回顾几条数学公式，后面的推导中我们将多次运用到这几条公式：
$$\begin{equation}\begin{aligned}
&\tanh x = 2\sigma(2x) - 1\\
&\sigma(x) = \frac{1}{2}\left(\tanh \frac{x}{2} + 1\right)\\
&(\tanh x)' = 1 - \tanh^2 x\\
&\sigma'(x) = \sigma(x)\left(1 - \sigma(x)\right)
\end{aligned}\end{equation}$$
其中$\sigma(x) = 1/(1+e^{-x})$是sigmoid函数。这几条公式其实就是说了这么一件事：$\tanh x$和$\sigma(x)$基本上是等价的，它们的导数均可以用它们自身来表示。

简单RNN分析 #

首先登场的是比较原始的简单RNN（有时候我们确实直接称它为SimpleRNN），它的公式为：
\begin{equation}h_t = \tanh \left(Wx_t + Uh_{t-1} + b\right)\end{equation}
其中$W,U,b$是待优化参数。看到这里很自然就能提出第一个疑问：为什么激活函数用$\tanh$而不是更流行的$\text{relu}$？这是个好问题，我们很快就会回答它。

从上面的讨论中我们已经知道，梯度消失还是爆炸主要取决于$\left|\frac{\partial h_t}{\partial h_{t-1}}\right|$，所以我们计算
\begin{equation}\frac{\partial h_t}{\partial h_{t-1}} = \left(1-h_t^2\right)U\label{eq:rnn-g}\end{equation}
由于我们无法确定$U$的范围，因此$\left|\frac{\partial h_t}{\partial h_{t-1}}\right|$可能小于1也可能大于1，梯度消失/爆炸的风险是存在的。但有意思的是，如果$|U|$很大，那么相应地$h_t$就会很接近1或-1，这样$\left(1-h_t^2\right)U$反而会小，事实上可以严格证明：如果固定$h_{t-1}\neq 0$，那么$\left(1-h_t^2\right)U$作为$U$的函数是有界的，也就是说不管$U$等于什么，它都不超过一个固定的常数。

这样一来，我们就能回答为什么激活函数要用$\tanh$了，因为激活函数用$\tanh$后，对应的梯度$\frac{\partial h_t}{\partial h_{t-1}}$是有界的，虽然这个界未必是1，但一个有界的量不超过1的概率总高于无界的量，因此梯度爆炸的风险更低。相比之下，如果用$\text{relu}$激活的话，它在正半轴的导数恒为1，此时$\frac{\partial h_t}{\partial h_{t-1}}=U$是无界的，梯度爆炸风险更高。

所以，RNN用$\text{tanh}$而不是$\text{relu}$的主要目的就是缓解梯度爆炸风险。当然，这个缓解是相对的，用了$\tanh$依然有爆炸的可能性。事实上，处理梯度爆炸的最根本方法是参数裁剪或梯度裁剪，换句话说我人为地把$U$给裁剪到$[-1,1]$内，那不就可以保证梯度不爆了吗？当然，又有读者会问，既然裁剪可以解决问题，那么是不是可以用$\text{relu}$了？确实是这样子，配合良好的初始化方法和参数/梯度裁剪方案，$\text{relu}$版的RNN也可以训练好，但是我们还是愿意用$\tanh$，这还是因为它对应的$\frac{\partial h_t}{\partial h_{t-1}}$有界，要裁剪也不用裁剪得太厉害，模型的拟合能力可能会更好。

LSTM的结果 #

当然，裁剪的方式虽然也能work，但终究是无奈之举，况且裁剪也只能解决梯度爆炸问题，解决不了梯度消失，如果能从模型设计上解决这个问题，那么自然是最好的。传说中的LSTM就是这样的一种设计，真相是否如此？我们马上来分析一下。

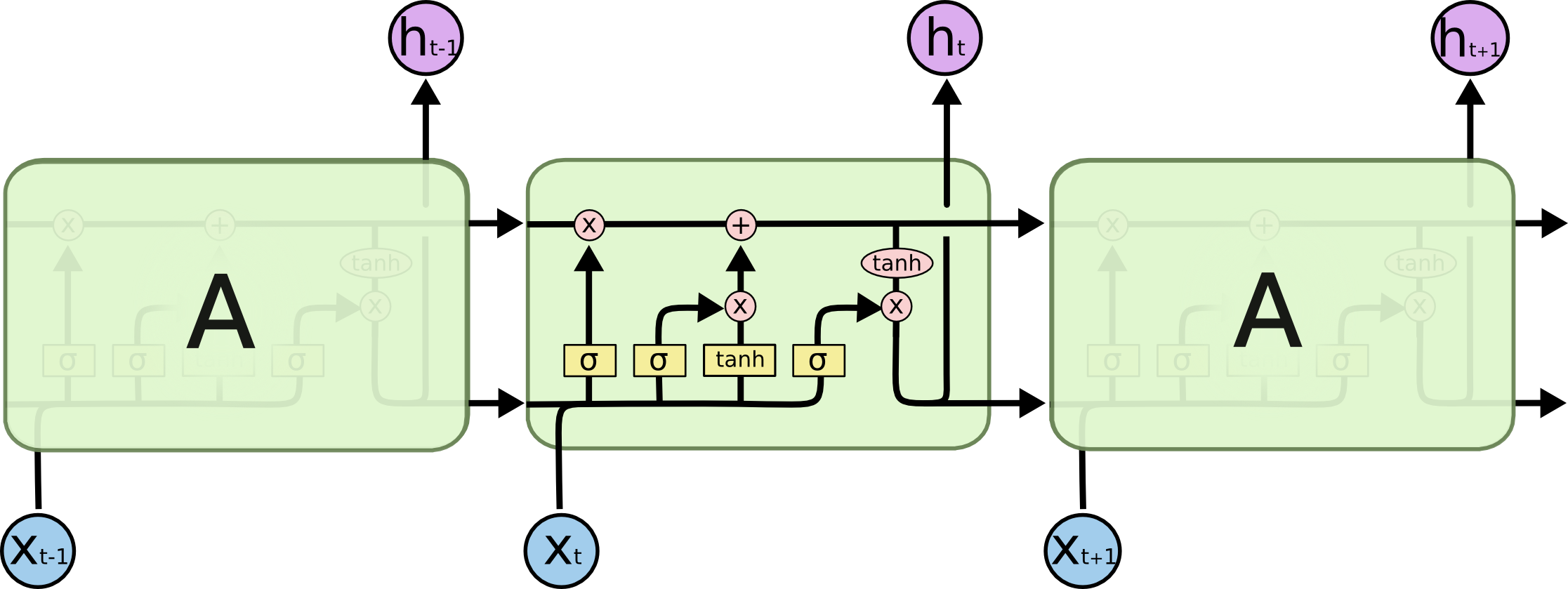
LSTM的更新公式比较复杂，它是：
\begin{equation}\begin{aligned} f_{t} & = \sigma \left( W_{f} x_{t} + U_{f} h_{t - 1} + b_{f} \right) \\
i_{t} & = \sigma \left( W_{i} x_{t} + U_{i} h_{t - 1} + b_{i} \right) \\
o_{t} & = \sigma \left( W_{o} x_{t} + U_{o} h_{t - 1} + b_{o} \right) \\
\hat{c}_t & = \tanh \left( W_{c} x_{t} + U_{c} h_{t - 1} + b_{c} \right)\\
c_{t} & = f_{t} \circ c_{t - 1} + i_{t} \circ \hat{c}_t \\
h_{t} & = o_{t} \circ \tanh \left( c_{t} \right)\end{aligned}\end{equation}
我们可以像上面一样计算$\frac{\partial h_t}{\partial h_{t-1}}$，但从$h_{t} = o_{t} \circ \tanh \left( c_{t} \right)$可以看出分析$c_{t}$就等价于分析$h_{t}$，而计算$\frac{\partial c_t}{\partial c_{t-1}}$显得更加简单一些，因此我们往这个方向走。

同样地，我们先只关心1维的情形，这时候根据求导公式，我们有
\begin{equation}\frac{\partial c_t}{\partial c_{t-1}}=f_t + c_{t-1}\frac{\partial f_t}{\partial c_{t-1}}+ \hat{c}_{t}\frac{\partial i_t}{\partial c_{t-1}}+ i_{t}\frac{\partial \hat{c}_t}{\partial c_{t-1}}\end{equation}
右端第一项$f_t$，也就是我们所说的“遗忘门”，从下面的论述我们可以知道一般情况下其余三项都是次要项，因此$f_t$是“主项”，由于$f_t$在0～1之间，因此就意味着梯度爆炸的风险将会很小，至于会不会梯度消失，取决于$f_t$是否接近于1。但非常碰巧的是，这里有个相当自洽的结论：如果我们的任务比较依赖于历史信息，那么$f_t$就会接近于1，这时候历史的梯度信息也正好不容易消失；如果$f_t$很接近于0，那么就说明我们的任务不依赖于历史信息，这时候就算梯度消失也无妨了。

所以，现在的关键就是看“其余三项都是次要项”这个结论能否成立。后面的三项都是“一项乘以另一项的偏导”的形式，而且求偏导的项都是$\sigma$或$\tanh$激活，前面在回顾数学公式的时候说了$\sigma$和$\tanh$基本上是等价的，因此后面三项是类似的，分析了其中一项就相当于分析了其余两项。以第二项为例，代入$h_{t-1} = o_{t-1} \tanh \left( c_{t-1} \right)$，可以算得
\begin{equation}c_{t-1}\frac{\partial f_t}{\partial c_{t-1}}=f_t \left(1 - f_t\right) o_{t-1} \left(1-\tanh^2 c_{t-1}\right)c_{t-1}U_f\end{equation}
注意到$f_t,1 - f_t,o_{t-1},$都是在0～1之间，也可以证明$\left|\left(1-\tanh^2 c_{t-1}\right)c_{t-1}\right| < 0.45$，因此它也在-1～1之间。所以$c_{t-1}\frac{\partial f_t}{\partial c_{t-1}}$就相当于1个$U_f$乘上4个门，结果会变得更加小，所以只要初始化不是很糟糕，那么它都会被压缩得相当小，因此占不到主导作用。跟简单RNN的梯度$\eqref{eq:rnn-g}$相比，它多出了3个门，所以这个变化说白点就是：1个门我压不垮你，多来几个门还不行么？

剩下两项的结论也是类似的：
\begin{equation}\begin{aligned}
\hat{c}_{t}\frac{\partial i_t}{\partial c_{t-1}}=&\,i_t \left(1 - i_t\right) o_{t-1} \left(1-\tanh^2 c_{t-1}\right)\hat{c}_{t}U_i\\
i_{t}\frac{\partial \hat{c}_t}{\partial c_{t-1}}=&\,\left(1 - \hat{c}_t^2\right) o_{t-1} \left(1-\tanh^2 c_{t-1}\right)i_{t}U_c
\end{aligned}\end{equation}

所以，后面三项的梯度带有更多的“门”，一般而言乘起来后会被压缩的更厉害，因此占主导的项还是$f_t$，$f_t$在0～1之间这个特性决定了它梯度爆炸的风险很小，同时$f_t$表明了模型对历史信息的依赖性，也正好是历史梯度的保留程度，两者相互自洽，所以LSTM也能较好地缓解梯度消失问题。因此，LSTM同时较好地缓解了梯度消失/爆炸问题，现在我们训练LSTM时，多数情况下只需要直接调用Adam等自适应学习率优化器，不需要人为对梯度做什么调整了。

当然，这些结果都是“概论”，你非要构造一个会梯度消失/爆炸的LSTM来，那也是能构造出来的。此外，就算LSTM能缓解这两个问题，也是在一定步数内，如果你的序列很长，比如几千上万步，那么该消失的还会消失。毕竟单靠一个向量，也缓存不了那么多信息啊～

顺便看看GRU #

在文章结束之前，我们顺便对LSTM的强力竞争对手GRU也做一个分析。GRU的运算过程为：
\begin{equation}\begin{aligned} z_{t} & = \sigma \left( W_{z} x_{t} + U_{z} h_{t - 1} + b_{z} \right) \\
r_{t} & = \sigma \left( W_{r} x_{t} + U_{r} h_{t - 1} + b_{r} \right) \\
\hat{h}_t & = \tanh \left( W_{h} x_{t} + U_{h} (r_t \circ h_{t - 1}) + b_{c} \right)\\
h_{t} & = \left(1 - z_{t}\right) \circ h_{t - 1} + z_{t} \circ \hat{h}_t \end{aligned}\end{equation}
还有个更极端的版本是将$r_t,z_t$合成一个：
\begin{equation}\begin{aligned}
r_{t} & = \sigma \left( W_{r} x_{t} + U_{r} h_{t - 1} + b_{r} \right) \\
\hat{h}_t & = \tanh \left( W_{h} x_{t} + U_{h} (r_t \circ h_{t - 1}) + b_{c} \right)\\
h_{t} & = \left(1 - r_{t}\right) \circ h_{t - 1} + r_{t} \circ \hat{h}_t \end{aligned}\end{equation}
不管是哪一个，我们发现它在算$\hat{h}_t$的时候，$h_{t-1}$都是先乘个$r_t$变成$r_t \circ h_{t - 1}$，不知道读者是否困惑过这一点？直接用$h_{t-1}$不是更简洁更符合直觉吗？

首先我们观察到，而$h_0$一般全零初始化，$\hat{h}_t$则因为$\tanh$激活，因此结果必然在-1～1之间，所以作为$h_{t-1}$与$\hat{h}_t$的加权平均的$h_{t}$也一直保持在-1～1之间，因此$h_t$本身就有类似门的作用。这跟LSTM的$c_t$不一样，理论上$c_t$是有可能发散的。了解到这一点后，我们再去求导：
\begin{equation}\begin{aligned}
\frac{\partial h_t}{\partial h_{t-1}} =& 1 - z_t - z_t (1-z_t) h_{t-1} U_z + z_t (1-z_t) \hat{h}_{t} U_z \\
& + \left(1-\hat{h}_{t}^2\right)r_t\left(1 + (1 - r_t)h_{t-1}U_r\right) z_t U_h
\end{aligned}\end{equation}
其实结果跟LSTM的类似，主导项应该是$1-z_t$，但剩下的项比LSTM对应的项少了1个门，因此它们的量级可能更大，相对于LSTM的梯度其实更不稳定，特别是$r_t \circ h_{t - 1}$这步操作，虽然给最后一项引入了多一个门$r_t$，但也同时引入了多一项$1 + (1 - r_t)h_{t - 1}U_r$，是好是歹很难说。总体相对而言，感觉GRU应该会更不稳定，比LSTM更依赖于好的初始化方式。

针对上述分析结果，个人认为如果沿用GRU的思想，又需要简化LSTM并且保持LSTM对梯度的友好性，更好的做法是把$r_t \circ h_{t - 1}$放到最后：
\begin{equation}\begin{aligned} z_{t} & = \sigma \left( W_{z} x_{t} + U_{z} h_{t - 1} + b_{z} \right) \\
r_{t} & = \sigma \left( W_{r} x_{t} + U_{r} h_{t - 1} + b_{r} \right) \\
\hat{c}_t & = \tanh \left( W_{h} x_{t} + U_{h} h_{t - 1} + b_{c} \right)\\
c_{t} & = \left(1 - z_{t}\right) \circ c_{t - 1} + z_{t} \circ \hat{c}_t \\
h_t & = r_t \circ c_t\end{aligned}\end{equation}
当然，这样需要多缓存一个变量，带来额外的显存消耗了。

文章总结概述 #

本文讨论了RNN的梯度消失/爆炸问题，主要是从梯度函数的有界性、门控数目的多少来较为明确地讨论RNN、LSTM、GRU等模型的梯度流情况，以确定其中梯度消失/爆炸风险的大小。本文属于闭门造车之作，如有错漏，请读者海涵并斧正。

转载到请包括本文地址：https://kexue.fm/archives/7888

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。