突破瓶颈，打造更强大的Transformer

自《Attention is All You Need》一文发布后，基于Multi-Head Attention的Transformer模型开始流行起来，而去年发布的BERT模型更是将Transformer模型的热度推上了又一个高峰。当然，技术的探索是无止境的，改进的工作也相继涌现：有改进预训练任务的，比如XLNET的PLM、ALBERT的SOP等；有改进归一化的，比如Post-Norm向Pre-Norm的改变，以及T5中去掉了Layer Norm里边的beta参数等；也有改进模型结构的，比如Transformer-XL等；有改进训练方式的，比如ALBERT的参数共享等；...

以上的这些改动，都是在Attention外部进行改动的，也就是说它们都默认了Attention的合理性，没有对Attention本身进行改动。而本文我们则介绍关于两个新结果：它们针对Multi-Head Attention中可能存在建模瓶颈，提出了不同的方案来改进Multi-Head Attention。两篇论文都来自Google，并且做了相当充分的实验，因此结果应该是相当有说服力的了。

再小也不能小key_size #

第一个结果来自文章《Low-Rank Bottleneck in Multi-head Attention Models》，它明确地指出了Multi-Head Attention里边的表达能力瓶颈，并提出通过增大key_size的方法来缓解这个瓶颈。

Multi-Head Attention #

首先简单回顾一下Multi-Head Attention，读者也可以翻看旧作《Attention is All You Need》浅读（简介+代码）。Multi-Head Attention的基础是自然是Single-Head Attention，也叫Scaled-Dot Attention，定义如下：
\begin{equation}Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = softmax\left(\frac{\boldsymbol{Q}\boldsymbol{K}^{\top}}{\sqrt{d_k}}\right)\boldsymbol{V}\end{equation}
其中$\boldsymbol{Q}\in\mathbb{R}^{n\times d_k}, \boldsymbol{K}\in\mathbb{R}^{m\times d_k}, \boldsymbol{V}\in\mathbb{R}^{m\times d_v}$。而Multi-Head Attention，就是将$\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}$分别用$h$个不同的投影矩阵投影$h$次，然后分别做$h$次Single-Head Attention，最后把结果拼接起来，即
\begin{equation}\begin{aligned}&\boldsymbol{Q}^{(1)}=\boldsymbol{Q}\boldsymbol{W}_Q^{(1)},\boldsymbol{K}^{(1)}=\boldsymbol{K}\boldsymbol{W}_K^{(1)},\boldsymbol{V}^{(1)}=\boldsymbol{V}\boldsymbol{W}_V^{(1)},\boldsymbol{O}^{(1)}=Attention\left(\boldsymbol{Q}^{(1)},\boldsymbol{K}^{(1)},\boldsymbol{V}^{(1)}\right)\\
&\boldsymbol{Q}^{(2)}=\boldsymbol{Q}\boldsymbol{W}_Q^{(2)},\boldsymbol{K}^{(2)}=\boldsymbol{K}\boldsymbol{W}_K^{(2)},\boldsymbol{V}^{(2)}=\boldsymbol{V}\boldsymbol{W}_V^{(2)},\boldsymbol{O}^{(2)}=Attention\left(\boldsymbol{Q}^{(2)},\boldsymbol{K}^{(2)},\boldsymbol{V}^{(2)}\right)\\
&\qquad\qquad\qquad\qquad\vdots\\
&\boldsymbol{Q}^{(h)}=\boldsymbol{Q}\boldsymbol{W}_Q^{(h)},\boldsymbol{K}^{(h)}=\boldsymbol{K}\boldsymbol{W}_K^{(h)},\boldsymbol{V}^{(h)}=\boldsymbol{V}\boldsymbol{W}_V^{(h)},\boldsymbol{O}^{(h)}=Attention\left(\boldsymbol{Q}^{(h)},\boldsymbol{K}^{(h)},\boldsymbol{V}^{(h)}\right)\\
&\boldsymbol{O}=\left[\boldsymbol{O}^{(1)},\boldsymbol{O}^{(2)},\dots,\boldsymbol{O}^{(h)}\right]
\end{aligned}\end{equation}

Attention里有个瓶颈 #

在实际使用中，$\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}$一般具有相同的特征维度$d_k=d_v=d$（即hidden_size），比如BERT Base里边是768；$h$一般选择12、16、24等，比如BERT base里边是12；确定了$d,h$之后，通常的选择是让投影矩阵$\boldsymbol{W}\in\mathbb{R}^{d\times (d/h)}$，也就是说，每个Attention Head里边，是将原始的$d$维投影到$d/h$维，然后在进行Attention运算，输出也是$d/h$维，最后把$h$个$d/h$维的结果拼接起来，得到一个$d$维的输出。这里的$d/h$我们通常称为head_size。

在Attention中，关键的一步是
\begin{equation}\boldsymbol{P}=softmax\left(\frac{\boldsymbol{Q}\boldsymbol{K}^{\top}}{\sqrt{d_k}}\right)\label{eq:softmax}\end{equation}
这一步是描述了$\boldsymbol{Q}$与$\boldsymbol{K}$的两两向量之间的联系，我们可以将$\boldsymbol{P}$看成一个二元联合分布（实际上是$n$个一元分布，不过这个细节并不重要），如果序列长度都为$n$，也就是每个元有$n$个可能的取值，那么这个分布共有$n^2$个值。

但是，我们将$\boldsymbol{Q},\boldsymbol{K}$分别投影到低维后，各自的参数量只有$n\times (d/h)$，总的参数量是$2nd/h$，所以式$\eqref{eq:softmax}$就相当于用$2nd/h$的参数量去逼近一个本身有$n^2$个值的量，而我们通常有$2nd/h \ll n^2$，尤其是$h$比较大时更是如此，因此这种建模有点“强模型所难”，这就是原论文中的“低秩瓶颈（Low-Rank Bottleneck）”的含义。

不妨试试增大key_size？ #

那么，解决办法是什么呢？直接的想法是让$2nd/h$增大，所以要不就是减少head的数目$h$，要不就是增加hidden_size大小$d$。但是更多的Attention Head本身也能增强模型的表达能力，所以为了缓解低秩瓶颈而减少$h$的做法可能得不偿失；如果增加$d$的话，那自然是能够增强模型整体表达能力的，但整个模型的规模与计算量也会剧增，似乎也不是一个好选择。

那没有其他办法了吗？有！当我们用投影矩阵将$\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}$都投影到低维时，前面都是将它们投影到$d/h$维，但其实它们的维度不一定要相等，而是只需要保证$\boldsymbol{Q},\boldsymbol{K}$的维度相等就行了（因为要做内积），为了区别，我们通常称$\boldsymbol{Q},\boldsymbol{K}$的维度为key_size，$\boldsymbol{V}$的维度才叫head_size，改变key_size的大小而不改变head_size的话，也不影响模型的hidden_size。

所以，这篇论文提出来的解决方法就是增大模型的key_size，它能增加Attention的表达能力，并且不改变模型整体的hidden_size，计算量上也只是稍微增加了一点。

补充说明：

事实上原论文考虑的是同时增大key_size和head_size、然后Multi-Head Attention的输出拼接之后再用一个变换矩阵降维，但笔者认为由于拼接降维这一步只是一个线性变换，所以本质上的提升还是来源于增大key_size，所以本文只强调了增大key_size这一步。

此外，如果同时增大key_size和head_size，那么会导致计算量和显存消耗都明显增加，而只增大key_size的话，增加的资源消耗就小很多了。

来看看实验结果～ #

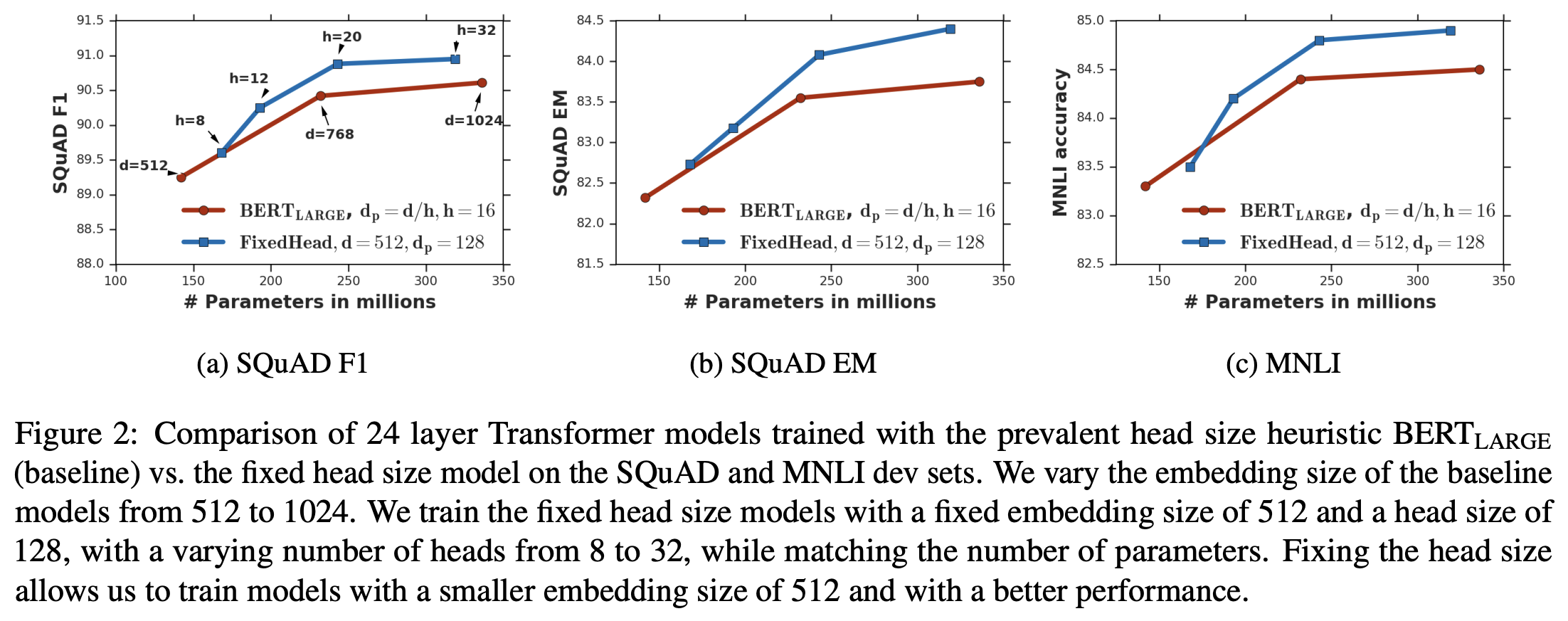
增大key_size这个想法很简单，也容易实现，但是否真的有效呢？我们来看看原论文的实验结果，其实验都是以BERT为baseline的，实验结果图表很多，大家直接看原论文为好，这里只分享比较有代表性的一个：

保持一个较大的key_size，能使得模型在同样参数规模的情况下表现更优异

这个结果显示，如果固定一个比较大的key_size（比如128），那么我们可以调整模型的hidden_size和head数，使得参数量可以跟原始的BERT设计一致，但是效果更优！所以，增加key_size确实是有意义的，哪怕将总体参数量重新调整到原来的一样大，也能一定程度上提升模型的效果。这无疑对我们设计新的Transformer模型（尤其是小规模的模型）有重要的指导作用。

最后，附上我们预训练的两个增大了key_size的RoBERTa小模型，欢迎大家使用（我们称之为RoBERTa⁺）：

https://github.com/ZhuiyiTechnology/pretrained-models

再缺也不能缺Talking #

对Multi-Head Attention改进的第二个结果来自论文《Talking-Heads Attention》，这篇论文虽然没有显式地指出它跟前一篇论文的联系，但笔者认为它们事实上在解决同一个问题，只不过思路不一样：它指出当前的Multi-Head Attention每个head的运算是相互孤立的，而通过将它们联系（Talking）起来，则可以得到更强的Attention设计，即标题的“Talking-Heads Attention”。

从单一分布到混合分布 #

在前一篇论文里边，我们提到了低秩瓶颈，也就是由于key_size太小所以$\boldsymbol{Q}^{(i)}{\boldsymbol{K}^{(i)}}^{\top}$表达能力不足，因此softmax之后无法很好地建议完整的二元分布。为了缓解这个问题，除了增大key_size之外，还有没有其他方法呢？有，比如这篇论文使用的混合分布思路。

所谓混合分布，就是多个简单分布的叠加（比如加权平均），它能极大地增强原分布的表达能力。典型的例子是高斯混合模型：我们知道高斯分布只是一个常见的简单分布，但多个高斯分布叠加而成的高斯混合分布（也叫高斯混合模型，GMM）就是一个更强的分布，理论上来说，只要叠加的高斯分布足够多，高斯混合分布能逼近任意概率分布。这个例子告诉我们，想要增加Attention中分布的表达能力，又不想增加key_size，那么可以考虑叠加多个低秩分布。

那么“多个”低秩分布哪里来呢？不是有Multi-Head嘛，每个head都带有一个低秩分布，就直接用它们叠加就行了，这就是Talking-Heads Attention了。具体来说，它的形式是：
\begin{equation}\begin{aligned}&\hat{\boldsymbol{J}}^{(1)}=\boldsymbol{Q}^{(1)}{\boldsymbol{K}^{(1)}}^{\top},\quad\hat{\boldsymbol{J}}^{(2)}=\boldsymbol{Q}^{(2)}{\boldsymbol{K}^{(2)}}^{\top},\quad\cdots,\quad\hat{\boldsymbol{J}}^{(h)}=\boldsymbol{Q}^{(h)}{\boldsymbol{K}^{(h)}}^{\top}\\
&\begin{pmatrix}\boldsymbol{J}^{(1)} \\ \boldsymbol{J}^{(2)} \\ \vdots \\ \boldsymbol{J}^{(h)}\end{pmatrix}=\begin{pmatrix}\lambda_{11} & \lambda_{12}& \cdots & \lambda_{1h}\\
\lambda_{21} & \lambda_{22} & \cdots & \lambda_{2h}\\
\vdots & \vdots & \ddots & \vdots\\
\lambda_{h1} & \lambda_{h2} & \cdots & \lambda_{hh}
\end{pmatrix}\begin{pmatrix}\hat{\boldsymbol{J}}^{(1)} \\ \hat{\boldsymbol{J}}^{(2)} \\ \vdots \\ \hat{\boldsymbol{J}}^{(h)}\end{pmatrix}\\
&\boldsymbol{P}^{(1)}=softmax\left(\boldsymbol{J}^{(1)}\right),\boldsymbol{P}^{(2)}=softmax\left(\boldsymbol{J}^{(2)}\right),\dots,\boldsymbol{P}^{(h)}=softmax\left(\boldsymbol{J}^{(h)}\right)\\
&\boldsymbol{O}^{(1)}=\boldsymbol{P}^{(1)} \boldsymbol{V}^{(1)},\quad \boldsymbol{O}^{(2)}=\boldsymbol{P}^{(2)} \boldsymbol{V}^{(2)},\quad ,\cdots,\quad\boldsymbol{O}^{(h)}=\boldsymbol{P}^{(h)} \boldsymbol{V}^{(h)}\\
&\boldsymbol{O}=\left[\boldsymbol{O}^{(1)},\boldsymbol{O}^{(2)},\dots,\boldsymbol{O}^{(h)}\right]
\end{aligned}\end{equation}
写起来很复杂，事实上很简单，就是在“$\boldsymbol{Q}\boldsymbol{K}^{\top}$之后、softmax之前”用一个参数矩阵$\boldsymbol{\lambda}$将各个$\boldsymbol{Q}\boldsymbol{K}^{\top}$的结果叠加一下而已。这样就把原本是孤立的各个Attention Head联系了起来，即做了一个简单的Talking。

对上述公式，做两点补充说明：

1、简单起见，上述公式中笔者省去了缩放因子$\sqrt{d_k}$，如果有需要，读者自行补充上去即可；

2、更一般的Talking-Heads Attention允许可以在$\boldsymbol{J}=\boldsymbol{\lambda}\hat{\boldsymbol{J}}$这一步进行升维，即叠加出多于$h$个混合分布，然后再用另一个参数矩阵降维，但这并不是特别重要的改进，所以不在主要篇幅介绍。

再来看看实验结果～ #

是不是真的有效，当然还是得靠实验结果来说话。这篇论文的实验阵容可谓空前强大，它同时包含了BERT、ALBERT、T5为baseline的实验结果！众所周知，BERT、ALBERT、T5均是某个时间段的NLP最优模型，尤其是T5还是处在superglue的榜首，并且远超出第二名很多，而这个Talking-Heads Attention则几乎是把它们的辉煌战绩又刷到了一个新高度！

还是那句话，具体的实验结果大家自己看论文去，这里展示一个比较典型的结果：

实验结果显示，采用Talking-Head机制的情况下，保持hidden_size不变的情况下，head的数目越大，结果越优

这个结果显示，使用Talking-Head Attention情况下，保持hidden_size不变，head数目越大（相应地key_size和head_size都越小），效果越优。这看起来跟前一篇增大key_size的结论矛盾，但事实上这正说明了混合分布对分布拟合能力明显提升作用，能够将key_size缩小时本身变弱的单一分布，叠加成拟合能力更强大的分布。当然，这不能说明就直接设key_size=1就好了，因为key_size=1时计算量会明显大于原始的BERT base，应用时需要根据实际情况平衡效果和计算量。

上述表格只是原论文实验结果的冰山一角，这里再放出一个实验表格，让大家感受感受它的实验阵容：

T5 + Talking-Heads Attention 在SuperGLUE上的实验结果

几乎每个任务、每个超参组合都做了实验，并给出实验结果。如此强大的实验阵容，基本上也就只有Google能搞出来了，而且整篇论文明显是浓浓的“T5 Style”（还没看过T5论文的读者，可以去《Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer》感受一下），果不其然，作者之一Noam Shazeer也正是T5的作者之一。

笔者只想说，这种庞大的实验轰炸，仿佛在向我们宣告着：

不用质疑，该调的参数我们都调了，就我们的Talking-Heads Attention最好～

插曲：神奇的论文画风 #

话说回来，笔者在Arxiv上首次刷到《Talking-Heads Attention》这篇论文时，第一感觉是一篇垃圾论文。为啥？因为它的画风是这样的：

《Talking-Heads Attention》里边的伪代码

谁能想象到，一篇如此强大的论文，里边居然没有一条数学公式，取而代之的全是伪代码！！其实伪代码都算不上，感觉更像是直接把实验中的Python代码复制到了论文中，还是复制到论文主体上！笔者印象里，只有那些不入流的水论文才会这样做，所以笔者看到的第一想法就是水文一篇。也就Google的大佬们才能这么任性，要不是耐着心多扫了几眼，要不是不小心扫到了T5等字眼，要不是回去看作者居然清一色是Google的，这篇强大的论文就被笔者当作垃圾论文放到回收站了。

不过，任性还是有任性的代价的，这篇实验阵容这么强大又这么有效的论文，发布至今也有一个多月了，但似乎也没什么反响，估计也跟这个任性的风格有关系～

来自文末的小结 #

本文介绍了两个关于Multi-Head Attention的后续改进工作，虽然改进细节不一致，但可以说它们都是针对“低秩瓶颈”这个问题而提出的，有种殊途同归之感。两个工作都来自Google，实验内容都很丰富，所以结果都比较有说服力，正在做模型结构改进工作的读者可以参考参考。

转载到请包括本文地址：https://kexue.fm/archives/7325

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。