揭开迷雾,来一顿美味的Capsule盛宴
By 苏剑林 | 2018-01-23 | 545156位读者 |由深度学习先驱Hinton开源的Capsule论文《Dynamic Routing Between Capsules》,无疑是去年深度学习界最热点的消息之一。得益于各种媒体的各种吹捧,Capsule被冠以了各种神秘的色彩,诸如“抛弃了梯度下降”、“推倒深度学习重来”等字眼层出不穷,但也有人觉得Capsule不外乎是一个新的炒作概念。
本文试图揭开让人迷惘的云雾,领悟Capsule背后的原理和魅力,品尝这一顿Capsule盛宴。同时,笔者补做了一个自己设计的实验,这个实验能比原论文的实验更有力说明Capsule的确产生效果了。
菜谱一览:
1、Capsule是什么?
2、Capsule为什么要这样做?
3、Capsule真的好吗?
4、我觉得Capsule怎样?
5、若干小菜。
前言 #
Capsule的论文已经放出几个月了,网上已经有很多大佬进行解读,也有大佬开源实现了CapsuleNet,这些内容都加速了我对Capsule的理解。然而,我觉得美中不足的是,网上多数的解读,都只是在论文的翻译上粉饰了一点文字,并没有对Capsule的原理进行解读。比如“动态路由”那部分,基本上就是照搬论文的算法,然后说一下迭代3次就收敛了。但收敛出什么来?论文没有说,解读也没有说,这显然是不能让人满意的。也难怪知乎上有读者评论说:
所谓的capsule为dl又贡献了一个花里胡哨的trick概念。说它是trick,因为hinton没有说为什么routing算法为什么需要那么几步,循环套着循环,有什么理论依据吗?还是就是凑出来的?
这个评论也许过激了,然而也是很中肯的:凭啥Hinton摆出来一套算法又不解释,我们就要稀里糊涂的跟着玩?
Capsule盛宴 #
宴会特色 #
这次Capsule盛宴的特色是“vector in vector out”,取代了以往的“scalar in scalar out”,也就是神经元的输入输出都变成了向量,从而算是对神经网络理论的一次革命。然而真的是这样子吗?难道我们以往就没有做过“vector in vector out”的任务了吗?有,而且多的是!NLP中,一个词向量序列的输入,不就可以看成“vector in”了吗?这个词向量序列经过RNN/CNN/Attention的编码,输出一个新序列,不就是“vector out”了吗?在目前的深度学习中,从来不缺乏“vector in vector out”的案例,因此显然这不能算是Capsule的革命。
Capsule的革命在于:它提出了一种新的“vector in vector out”的传递方案,并且这种方案在很大程度上是可解释的。
如果问深度学习(神经网络)为什么有效,我一般会这样回答:神经网络通过层层叠加完成了对输入的层层抽象,这个过程某种程度上模拟了人的层次分类做法,从而完成对最终目标的输出,并且具有比较好的泛化能力。的确,神经网络应该是这样做的,然而它并不能告诉我们它确确实实是这样做的,这就是神经网络的难解释性,也就是很多人会将深度学习视为黑箱的原因之一。
让我们来看Hinton是怎么来通过Capsule突破这一点的。
大盆菜 #
如果要用一道菜来比喻Capsule,我想到了“大盆菜”:
盆菜作为客家菜的菜式出现由来以久,一般也称为大盘菜,大盘菜源于客家人传统的“发财大盘菜”,顾名思义就是用一个大大的盘子,将食物都放到里面,融汇出一种特有滋味。丰富的材料一层层叠进大盘之中,最易吸收肴汁的材料通常放在下面。吃的时候每桌一盘,一层一层吃下去,汁液交融,味道馥郁而香浓,令人大有渐入佳景之快。
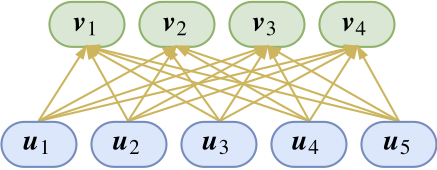
Capsule就是针对着这个“层层递进”的目标来设计的,但坦白说,Capsule论文的文笔真的不敢恭维,因此本文尽量不与论文中的符号相同,以免读者再次云里雾里。让我们来看个图。
如图所示,底层的胶囊和高层的胶囊构成一些连接关系。等等,什么是“胶囊”?其实,只要把一个向量当作一个整体来看,它就是一个“胶囊”,是的,你没看错,你可以这样理解:神经元就是标量,胶囊就是向量,就这么粗暴!Hinton的理解是:每一个胶囊表示一个属性,而胶囊的向量则表示这个属性的“标架”。也就是说,我们以前只是用一个标量表示有没有这个特征(比如有没有羽毛),现在我们用一个向量来表示,不仅仅表示有没有,还表示“有什么样的”(比如有什么颜色、什么纹理的羽毛),如果这样理解,就是说在对单个特征的表达上更丰富了。
说到这里,我感觉有点像NLP中的词向量,以前我们只是用one hot来表示一个词,也就是表示有没有这个词而已。现在我们用词向量来表示一个词,显然词向量表达的特征更丰富,不仅可以表示有没有,还可以表示哪些词有相近含义。词向量就是NLP中的“胶囊”?这个类比可能有点牵强,但我觉得意思已经对了。
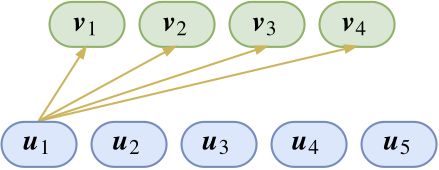
那么,这些胶囊要怎么运算,才能体现出“层层抽象”、“层层分类”的特性呢?让我们先看其中一部分连接:
图上只展示了$\boldsymbol{u}_1$的连接。这也就是说,目前已经有了$\boldsymbol{u}_1$这个特征(假设是羽毛),那么我想知道它属于上层特征$\boldsymbol{v}_1,\boldsymbol{v}_2,\boldsymbol{v}_3,\boldsymbol{v}_4$(假设分别代表了鸡、鸭、鱼、狗)中的哪一个。分类问题我们显然已经是很熟悉了,不就是内积后softmax吗?于是单靠$\boldsymbol{u}_1$这个特征,我们推导出它是属于鸡、鸭、鱼、狗的概率分别是
$$\big(p_{1|1},p_{2|1},p_{3|1},p_{4|1}\big) = \frac{1}{Z_1}\Big(e^{\langle\boldsymbol{u}_1,\boldsymbol{v}_1\rangle},
e^{\langle\boldsymbol{u}_1,\boldsymbol{v}_2\rangle},
e^{\langle\boldsymbol{u}_1,\boldsymbol{v}_3\rangle},
e^{\langle\boldsymbol{u}_1,\boldsymbol{v}_4\rangle}\Big)\tag{1}$$
我们当然期望$p_{1|1}$和$p_{2|1}$会明显大于$p_{3|1}$和$p_{4|1}$。不过,单靠这个特征还不够,我们还需要综合各个特征,于是可以把上述操作对各个$\boldsymbol{u}_i$都做一遍,继而得到$\big(p_{1|2},p_{2|2},p_{3|2},p_{4|2}\big)$、$\big(p_{1|3},p_{2|3},p_{3|3},p_{4|3}\big)$、...
问题是,现在得到这么多预测结果,那我究竟要选择哪个呢?而且我又不是真的要做分类,我要的是融合这些特征,构成更高级的特征。于是Hinton认为,既然$\boldsymbol{u}_i$这个特征得到的概率分布是$\big(p_{1|i},p_{2|i},p_{3|i},p_{4|i}\big)$,那么我把这个特征切成四份,分别为$\big(p_{1|i}\boldsymbol{u}_i,p_{2|i}\boldsymbol{u}_i,p_{3|i}\boldsymbol{u}_i,p_{4|i}\boldsymbol{u}_i\big)$,然后把这几个特征分别传给$\boldsymbol{v}_1,\boldsymbol{v}_2,\boldsymbol{v}_3,\boldsymbol{v}_4$,最后$\boldsymbol{v}_1,\boldsymbol{v}_2,\boldsymbol{v}_3,\boldsymbol{v}_4$其实就是各个底层传入的特征的累加,这样不就好了?
$$\boldsymbol{v}_j = squash\left(\sum_{i} p_{j|i} \boldsymbol{u}_i\right) = squash\left(\sum_{i} \frac{e^{\langle\boldsymbol{u}_i,\boldsymbol{v}_j\rangle}}{Z_i} \boldsymbol{u}_i\right)\tag{2}$$
从上往下看,那么Capsule就是每个底层特征分别做分类,然后将分类结果整合。这时$\boldsymbol{v}_j$应该尽量与所有$\boldsymbol{u}_i$都比较靠近,靠近的度量是内积。因此,从下往上看的话,可以认为$\boldsymbol{v}_j$实际上就是各个$\boldsymbol{u}_i$的某个聚类中心,而Capsule的核心思想就是输出是输入的某种聚类结果。
现在来看这个$squash$是什么玩意,它怎么来的呢?
浓缩果汁 #
squash在英文中也有浓缩果汁之意,我们就当它是一杯果汁品尝吧。这杯果汁的出现,是因为Hinton希望Capsule能有的一个性质是:胶囊的模长能够代表这个特征的概率。
其实我不喜欢概率这个名词,因为概率让我们联想到归一化,而归一化事实上是一件很麻烦的事情。我觉得可以称为是特征的“显著程度”,这就好解释了,模长越大,这个特征越显著。而我们又希望有一个有界的指标来对这个“显著程度”进行衡量,所以就只能对这个模长进行压缩了,所谓“浓缩就是精华”嘛。Hinton选取的压缩方案是:
$$squash(\boldsymbol{x})=\frac{\Vert\boldsymbol{x}\Vert^2}{1+\Vert\boldsymbol{x}\Vert^2}\frac{\boldsymbol{x}}{\Vert\boldsymbol{x}\Vert}\tag{3}$$
其中$\boldsymbol{x}/\Vert\boldsymbol{x}\Vert$是很好理解的,就是将模长变为1,那么前半部分怎么理解呢?为什么这样选择?事实上,将模长压缩到0~1的方案有很多,比如
$$\tanh \Vert\boldsymbol{x}\Vert, \quad 1-e^{-\Vert\boldsymbol{x}\Vert}, \quad \frac{\Vert\boldsymbol{x}\Vert}{1+\Vert\boldsymbol{x}\Vert}$$
等等,并不确定Hinton选择目前这个方案的思路。也许可以每个方案都探索一下?事实上,我在一些实验中发现,选择
$$squash(\boldsymbol{x})=\frac{\Vert\boldsymbol{x}\Vert^2}{0.5+\Vert\boldsymbol{x}\Vert^2}\frac{\boldsymbol{x}}{\Vert\boldsymbol{x}\Vert}$$
效果要好一点。这个函数的特点是在模长很接近于0时起到放大作用,而不像原来的函数那样全局都压缩。
然而,一个值得思考的问题是:如果在中间层,那么这个压缩处理是不是必要的呢?因为已经有了后面说的动态路由在里边,因此即使去掉$squash$函数,网络也已经具有了非线性了,因此直觉上并没有必要在中间层也引入特征压缩,正如普通神经网络也不一定要用sigmoid函数压缩到0~1。我觉得这个要在实践中好好检验一下。
动态路由 #
注意到$(2)$式,为了求$\boldsymbol{v}_j$需要求softmax,可是为了求softmax又需要知道$\boldsymbol{v}_j$,这不是个鸡生蛋、蛋生鸡的问题了吗?这时候就要上“主菜”了,即“动态路由”(Dynamic Routing),它能够根据自身的特性来更新(部分)参数,从而初步达到了Hinton的放弃梯度下降的目标。
这道“主菜”究竟是不是这样的呢?它是怎么想出来的?最终收敛到哪里去?让我们先上两道小菜,然后再慢慢来品尝这道主菜。
小菜1 #
让我们先回到普通的神经网络,大家知道,激活函数在神经网络中的地位是举足轻重的。当然,激活函数本身很简单,比如一个tanh激活的全连接层,用tensorflow写起来就是:
y = tf.matmul(W, x) + b
y = tf.tanh(y)可是,如果我想用$x = y + \cos y$的反函数来激活呢?也就是说,你得给我解出$y=f(x)$,然后再用它来做激活函数。
然而数学家告诉我们,这个东西的反函数是一个超越函数,也就是不可能用初等函数有限地表示出来。那这样不就是故意刁难么?不要紧,我们有迭代:
$$y_{n+1}=x-\cos y_n$$
选择$y_0 = x$,代入上式迭代几次,基本上就可以得到比较准确的$y$了。假如迭代三次,那就是
$$y=x-\cos\big(x-\cos(x-\cos x)\big)$$
用tensorflow写出来就是
y = tf.matmul(W, x) + b
Y = y
for i in range(3):
Y = y - tf.cos(Y)如果读者已经“预习”过Capsule,那么就会发现这跟Capsule的动态路由很像。
小菜2 #
再来看一个例子,这个例子可能在NLP中有很多对应的情景,但图像领域其实也不少。考虑一个向量序列$(\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_n)$,我现在要想办法将这$n$个向量整合成一个向量$\boldsymbol{x}$(encoder),然后用这个向量来做分类。
也许读者会想到用LSTM。但我这里仅仅想要将它表示为原来向量的线性组合,也就是:
$$\boldsymbol{x}=\sum_{i=1}^{n} \lambda_i \boldsymbol{x}_i$$
这里的$\lambda_i$相当于衡量了$\boldsymbol{x}$与$\boldsymbol{x}_i$的相似度。然而问题来了,在$\boldsymbol{x}$出现之前,凭什么能够确定这个相似度呢?这不也是一个鸡生蛋、蛋生鸡的问题吗?解决这个问题的一个方案也是迭代。首先我们也可以定义一个基于softmax的相似度指标,然后让
$$\boldsymbol{x}=\sum_{i=1}^{n} \frac{e^{\langle\boldsymbol{x},\boldsymbol{x}_i\rangle}}{Z} \boldsymbol{x}_i$$
一开始,我们一无所知,所以只好取$\boldsymbol{x}$为各个$\boldsymbol{x}_i$的均值,然后代入右边就可以算出一个$\boldsymbol{x}$,再把它代入右边,反复迭代就行,一般迭代有限次就可以收敛,于是就可以将这个迭代过程嵌入到神经网络中了。
如果说小菜1跟动态路由只是神似,那么小菜2已经跟动态路由是神似+形似了。不过我并没有看到已有的工作是这样做的,这个小菜只是我的头脑风暴。
上主菜~ #
其实有了这两个小菜,动态路由这道主菜根本就不神秘了。为了得到各个$\boldsymbol{v}_j$,一开始先让它们全都等于$\boldsymbol{u}_i$的均值,然后反复迭代就好。说白了,输出是输入的聚类结果,而聚类通常都需要迭代算法,这个迭代算法就称为“动态路由”。至于这个动态路由的细节,其实是不固定的,取决于聚类的算法,比如关于Capsule的新文章《MATRIX CAPSULES WITH EM ROUTING》就使用了Gaussian Mixture Model来聚类。
理解到这里,就可以写出本文的动态路由的算法了:
动态路由算法
初始化$b_{ij}=0$
迭代$r$次:
$\boldsymbol{c}_i \leftarrow softmax(\boldsymbol{b}_i)$;
$\boldsymbol{s}_j \leftarrow \sum\limits_i c_{ij} \boldsymbol{u}_i$;
$\boldsymbol{v}_j \leftarrow squash(\boldsymbol{s}_j)$;
$b_{ij} \leftarrow \langle\boldsymbol{u}_i,\boldsymbol{v}_j\rangle$。
返回$\boldsymbol{v}_j$。
这里的$c_{ij}$就是前文的$p_{j|i}$。
“嘿,终于逮到个错误了,我看过论文,应该是$b_{ij} \leftarrow b_{ij} + \langle\boldsymbol{u}_i,\boldsymbol{v}_j\rangle$而不是$b_{ij} \leftarrow \langle\boldsymbol{u}_i,\boldsymbol{v}_j\rangle$吧?”
事实上,上述算法并没有错——如果你承认本文的推导过程、承认$(2)$式的话,那么上述迭代过程就是没有错的。
“难道是Hinton错了?就凭你也有资格向Hinton叫板?”别急别急,先让我慢慢分析Hinton的迭代出现了什么问题。假如按照Hinton的算法,那么是$b_{ij} \leftarrow b_{ij} + \langle\boldsymbol{u}_i,\boldsymbol{v}_j\rangle$,从而经过$r$次迭代后,就变成了:
$$\boldsymbol{v}_j^{(r)}=squash\left(\sum_i\frac{e^{\big\langle\boldsymbol{u}_{i},\,\boldsymbol{v}_{j}^{(0)}+\boldsymbol{v}_{j}^{(1)}+\dots+\boldsymbol{v}_{j}^{(r-1)}\big\rangle}}{Z_i}\boldsymbol{u}_{i}\right)$$
由于$\boldsymbol{v}_j^{(r)}$会越来越接近真实的$\boldsymbol{v}_j$,那么我们可以写出
$$\boldsymbol{v}_j^{(r)}\sim squash\left(\sum_i\frac{e^{r\langle\boldsymbol{u}_{i},\,\boldsymbol{v}_j\rangle}}{Z_i}\boldsymbol{u}_{i}\right)$$
假如经过无穷多次迭代(实际上算力有限,做不到,但理论上总可以做到的),那么$r\to\infty$,这样的话softmax的结果是非零即1,也就是说,每个底层的胶囊仅仅联系到唯一一个上层胶囊。
这合理吗?我觉得不合理。不同的类别之间是有可能有共同的特征的,这就好比猫和狗虽然不一样,但是都有差不多的眼睛。对于这个问题,有些朋友是这样解释的:$r$是一个超参数,不能太大,太大了就容易过拟合。首先我不知道Hinton是不是也是同样的想法,但我认为,如果认为$r$是一个超参,那么这将会使得Capsule太丑陋了!
是啊,动态路由被来已经被很多读者评价为“不知所云”了,如果加上完全不符合直觉的超参,不就更加难看了吗?相反,如果换成本文的$(2)$式作为出发点,然后得到本文的动态路由算法,才能符合聚类的思想,而且在理论上会好看些,因为这时候就是$r$越大越好了(看算力而定),不存在这个超参。事实上,我改动了之后,在目前开源的Capsule源码上跑,也能跑到同样的结果。
至于读者怎么选择,就看读者的意愿吧。我自己是有点强迫症的,忍受不了理论上的不足。
模型细节 #
下面介绍Capsule实现的细节,对应的代码在我的Github中,不过目前只有Keras版。相比之前实现的版本,我的版本是纯Keras实现的(原来是半Keras半tensorflow),并通过K.local_conv1d函数替代了原作者使用的K.map_fn提升了好几倍的速度,这是因为K.map_fn并不会自动并行,要并行的话需要想办法整合到一个矩阵运算;其次我通过K.conv1d实现了共享参数版的。代码运行环境是Python2.7 + tensorflow 1.8 + keras 2.1.4。
全连接版 #
先不管是Hinton版还是我的版本,按照这个动态路由的算法,$\boldsymbol{v}_j$能够迭代地算出来,那不就没有参数了吗?真的抛弃了反向传播了?
非也非也~如果真的这样的话,各个$\boldsymbol{v}_j$都一样了。前面已经说了,$\boldsymbol{v}_j$是作为输入$\boldsymbol{u}_i$的某种聚类中心出现的,而从不同角度看输入,得到的聚类结果显然是不一样的。那么为了实现“多角度看特征”,于是可以在每个胶囊传入下一个胶囊之前,都要先乘上一个矩阵做变换,所以$(2)$式实际上应该要变为
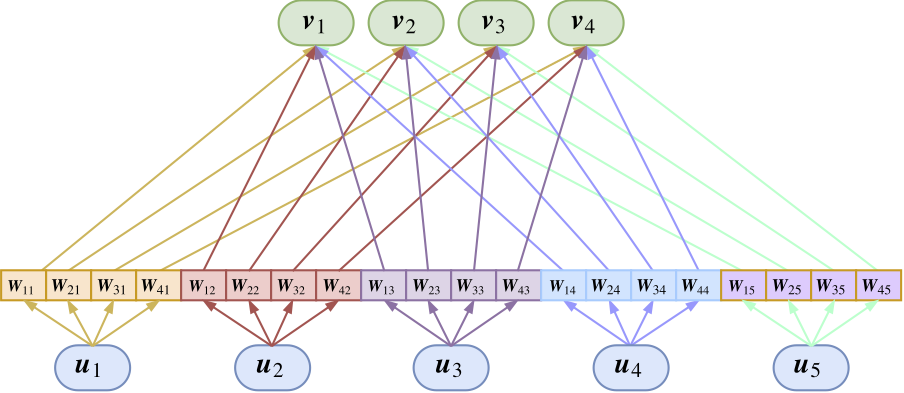
$$\boldsymbol{v}_j = squash\left(\sum_{i} \frac{e^{\langle\hat{\boldsymbol{u}}_{j|i},\,\boldsymbol{v}_j\rangle}}{Z_i} \hat{\boldsymbol{u}}_{j|i}\right),\quad \hat{\boldsymbol{u}}_{j|i} = \boldsymbol{W}_{ji}\boldsymbol{u}_i\tag{4}$$
这里的$\boldsymbol{W}_{ji}$是待训练的矩阵,这里的乘法是矩阵乘法,也就是矩阵乘以向量。所以,Capsule变成了下图
这时候就可以得到完整动态路由了
动态路由算法
初始化$b_{ij}=0$
迭代$r$次:
$\boldsymbol{c}_i \leftarrow softmax(\boldsymbol{b}_i)$;
$\boldsymbol{s}_j \leftarrow \sum\limits_i c_{ij} \hat{\boldsymbol{u}}_{j|i}$;
$\boldsymbol{v}_j \leftarrow squash(\boldsymbol{s}_j)$;
$b_{ij} \leftarrow \langle\hat{\boldsymbol{u}}_{j|i} , \boldsymbol{v}_j\rangle$。
返回$\boldsymbol{v}_j$。
这样的Capsule层,显然相当于普通神经网络中的全连接层。
共享版 #
众所周知,全连接层只能处理定长输入,全连接版的Capsule也不例外。而CNN处理的图像大小通常是不定的,提取的特征数目就不定了,这种情形下,全连接层的Capsule就不适用了。因为在前一图就可以看到,参数矩阵的个数等于输入输入胶囊数目乘以输出胶囊数目,既然输入数目不固定,那么就不能用全连接了。
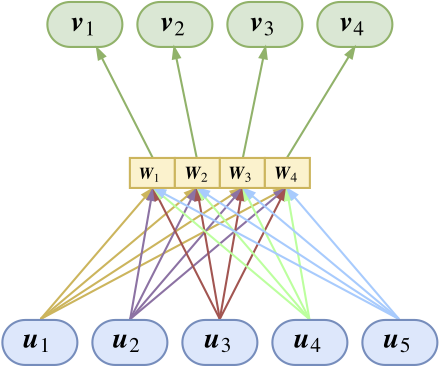
所以跟CNN的权值共享一样,我们也需要一个权值共享版的Capsule。所谓共享版,是指对于固定的上层胶囊$j$,它与所有的底层胶囊的连接的变换矩阵是共用的,即$\boldsymbol{W}_{ji}\equiv \boldsymbol{W}_j$,
如图所示,共享版其实不难理解,就是自下而上地看,就是所有输入向量经过同一个矩阵进行映射后,完成聚类进行输出,将这个过程重复几次,就输出几个向量(胶囊);又或者自上而下地看,将每个变换矩阵看成是上层胶囊的识别器,上层胶囊通过这个矩阵来识别出底层胶囊是不是有这个特征。因此很明显,这个版本的胶囊的参数量并不依赖于输入的胶囊个数,因此可以轻松接在CNN后面。对于共享版,$(2)$式要变为
$$\boldsymbol{v}_j = squash\left(\sum_{i} \frac{e^{\langle\hat{\boldsymbol{u}}_{j|i},\boldsymbol{v}_j\rangle}}{Z_i} \hat{\boldsymbol{u}}_{j|i}\right),\quad \hat{\boldsymbol{u}}_{j|i} = \boldsymbol{W}_{j}\boldsymbol{u}_i\tag{5}$$
至于动态路由算法就没有改变了。
反向传播 #
尽管我不是很喜欢反向传播这个名词,然而这里似乎不得不用上这个名字了。
现在又有了$\boldsymbol{W}_{ji}$,那么这些参数怎么训练呢?答案是反向传播。读者也许比较晕的是:现在既有动态路由,又有反向传播了,究竟两者怎么配合?其实这个真的就最简单不过了。就好像“小菜1”那样,把算法的迭代几步(论文中是3步),加入到模型中,从形式上来看,就是往模型中添加了三层罢了,剩下的该做什么还是什么,最后构建一个loss来反向传播。
这样看来,Capsule里边不仅有反向传播,而且只有反向传播,因为动态路由已经作为了模型的一部分,都不算在迭代算法里边了。
做了什么 #
是时候回顾一下了,Capsule究竟做了什么?其实用一种最直接的方式来讲,Capsule就是提供了一种新的“vector in vector out”的方案,这样看跟CNN、RNN、Attention层都没太大区别了;从Hinton的本意看,就是提供了一种新的、基于聚类思想来代替池化完成特征的整合的方案,这种新方案的特征表达能力更加强大。
实验 #
MNIST分类 #
不出意外地,Capsule首先被用在MNIST中做实验,然后效果还不错,通过扰动胶囊内的一些值来重构图像,确实发现这些值代表了某种含义,这也体现了Capsule初步完成了它的目标。
Capsule做分类模型,跟普通神经网络的一些区别是:Capsule最后输出10个向量(也就是10个胶囊),这10个向量各代表一类,每个向量的模长代表着它的概率。事实上,Capsule做的事情就是检测有没有这个类,也就是说,它把一个多分类问题转化为多个2分类问题。因此它并没有用普通的交叉熵损失,而是用了
$$L_c = T_c \max(0, m^+ − \Vert \boldsymbol{v}_c\Vert)^2 + \lambda (1 − T_c) \max(0, \Vert \boldsymbol{v}_c\Vert − m^−)^2$$
其中$T_c$非零即1,表明是不是这个类。当然这个没什么特殊性,也可以有多种选择。论文中还对比了加入重构网络后的提升。
总的来说,论文的实验有点粗糙,选择mnist来做实验显得有点不给力(好歹也得玩玩fashion mnist嘛),重构网络也只是简单粗暴地堆了两层全连接来做。不过就论文的出发点,应该只要能证明这个流程能work就好了,因此差强人意吧。
我的实验 #
由于普通的卷积神经网络下,mnist的验证集准确率都已经99%+了,因此如果就这样说Capsule起作用了,难免让人觉得不服气。这里我为Capsule设计了一个新实验,虽然这个实验也是基于mnist,但这个实验能很充分说明了Capsule具有良好的整合特征的能力。Capsule不仅work,还work得很漂亮。
实验是这样的:
1、通过现有的MNIST数据集,训练一个数字识别模型,但最后不用softmax做10分类,而是转化为10个2分类问题,显然,这个使用旧的CNN+Pooling或现在的CNN+Calsupe都能做;
2、训练完模型后,用模型进行测试。测试的图片并不是原始的测试集,是随机挑两张测试集的图片拼在一起,然后看模型能不能预测出这两个数字来(数字对即可,不考虑顺序)。
也就是说,训练集是1对1的,测试集是2对2的。
实验用Keras完成,完成的代码可见我的Github。这里仅仅展示核心部分。
首先是CNN。公平起见,大家的CNN模型都是一样的
#CNN部分,这部分两个模型都一致
input_image = Input(shape=(None,None,1))
cnn = Conv2D(64, (3, 3), activation='relu')(input_image)
cnn = Conv2D(64, (3, 3), activation='relu')(cnn)
cnn = AveragePooling2D((2,2))(cnn)
cnn = Conv2D(128, (3, 3), activation='relu')(cnn)
cnn = Conv2D(128, (3, 3), activation='relu')(cnn)然后先用普通的Pooling+全连接层进行建模:
cnn = GlobalAveragePooling2D()(cnn)
dense = Dense(128, activation='relu')(cnn)
output = Dense(10, activation='sigmoid')(dense)
model = Model(inputs=input_image, outputs=output)
model.compile(loss=lambda y_true,y_pred: y_true*K.relu(0.9-y_pred)**2 + 0.25*(1-y_true)*K.relu(y_pred-0.1)**2,
optimizer='adam',
metrics=['accuracy'])这个代码的参数量约为27万,能在mnist的标准测试集上达到99.3%以上的准确率,显然已经接近最佳状态。下面测试我们开始制定的任务,我们最后输出两个准确率:第一个准确率是取分数最高的两个类别;第二个准确率是取得分最高的两个类别,并且这两个类别的分数都要超过0.5才认可(因为是2分类)。代码如下:
#对测试集重新排序并拼接到原来测试集,就构成了新的测试集,每张图片有两个不同数字
idx = range(len(x_test))
np.random.shuffle(idx)
X_test = np.concatenate([x_test, x_test[idx]], 1)
Y_test = np.vstack([y_test.argmax(1), y_test[idx].argmax(1)]).T
X_test = X_test[Y_test[:,0] != Y_test[:,1]] #确保两个数字不一样
Y_test = Y_test[Y_test[:,0] != Y_test[:,1]]
Y_test.sort(axis=1) #排一下序,因为只比较集合,不比较顺序
Y_pred = model.predict(X_test) #用模型进行预测
greater = np.sort(Y_pred, axis=1)[:,-2] > 0.5 #判断预测结果是否大于0.5
Y_pred = Y_pred.argsort()[:,-2:] #取最高分数的两个类别
Y_pred.sort(axis=1) #排序,因为只比较集合
acc = 1.*(np.prod(Y_pred == Y_test, axis=1)).sum()/len(X_test)
print u'不考虑置信度的准确率为:%s'%acc
acc = 1.*(np.prod(Y_pred == Y_test, axis=1)*greater).sum()/len(X_test)
print u'考虑置信度的准确率为:%s'%acc
经过重复测试,如果不考虑置信度,那么准确率大约为40%,如果考虑置信度,那么准确率是10%左右。这是一组保守的数据,反复测试几次的话,很多时候连这两个数字都不到。
现在我们来看Capsule的表现,将CNN后面的代码替换成
capsule = Capsule(10, 16, 3, True)(cnn)
output = Lambda(lambda x: K.sqrt(K.sum(K.square(x), 2)))(capsule)
model = Model(inputs=input_image, outputs=output)
model.compile(loss=lambda y_true,y_pred: y_true*K.relu(0.9-y_pred)**2 + 0.25*(1-y_true)*K.relu(y_pred-0.1)**2,
optimizer='adam',
metrics=['accuracy'])这里用的就是共享权重版的Capsule,最后输出向量的模长作为分数,loss和optimizer都跟前面一致,代码的参数量也约为27万,在mnist的标准测试集上的准确率同样也是99.3%左右,这部分两者都差不多。
然而,让人惊讶的是:在前面所定制的新测试集上,Capsule模型的两个准确率都有90%以上!即使我们没有针对性地训练,但Capsule仍以高置信度给出了输入中包含的特征(即哪个数字)
当然,如果构造双数字的训练集让普通的CNN+Pooling训练,那么它也能work得很好,因此不是说旧的架构不能work,而是旧的架构迁移能力不够好。说白了,那就是普通的CNN+Pooling每一个任务都要“手把手”教才行,而Capsule则具有一定的举一反三的能力,后者是我们真正希望的。
思考 #
看起来还行 #
Capsule致力于给出神经网络的可解释的方案,因此,从这个角度来看,Capsule应该是成功的,至少作为测试版是很成功的。因为它的目标并不是准确率非常出众,而是对输入做一个优秀的、可解释的表征。从我上面的实验来看,Capsule也是很漂亮的,至少可以间接证明它比池化过程更接近人眼的机制。
事实上,通过向量的模长来表示概率,这一点让我想起了量子力学的波函数,它也是通过波函数的范数来表示概率的。这告诉我们,未来Capsule的发展也许可以参考一下量子力学的内容。
亟待优化 #
显然,Capsule可优化的地方还有非常多,包括理论上的和实践上的。我觉得整个算法中最不好看的部分并非动态路由,而是那个$squash$函数。对于非输出层,这个压缩究竟是不是必要的?还有,由于要用模长并表示概率,模长就得小于1,而两个模长小于1的向量加起来后模长不一定小于1,因此需要用函数进一步压缩,这个做法的主观性太强。这也许需要借助流形上的分析工具,才能给出更漂亮的解决方案,或者也可以借鉴一下量子力学的思路,因为量子力学也存在波函数相加的情况。
实践角度来看,Capsule显然是太慢了。这是因为将聚类的迭代过程(动态路由)嵌入了神经网络中。从前向传播来看,这并没有增加多少计算量,但从反向传播来看,计算量暴增了,因为复合函数的梯度会更加复杂。
反向传播好不好? #
Hinton想要抛弃反向传播的大概原因是:反向传播在生物中找不到对应的机制,因为反向传播需要精确地求导数。
事实上,我并不认同这种观点。尽管精确求导在自然界中很难存在,但这才意味着我们的先进。试想一下,如果不求导,那么我们也可以优化的,但需要“试探+插值”,比如将参数$\alpha$从3改为5后,发现loss变小了,于是我们就会想着试试$\alpha=7$,如果这时候loss变大了,我们就会想着试试$\alpha=6$。loss变小/大就意味着(近似的)梯度为负/正,这个过程的思想跟梯度下降是一致的,但这个过程一次性只能调节一个参数,而我们可能有数百万的参数要调,需要进行上百万次试验要才能完成每一个参数的调整。而求梯度,就是一种比重复试探更加高明的技巧,一次性作全部调整,何乐而不用呢?
池化好不好? #
Hinton认为卷积中的池化是不科学的,但我并不这样认为,池化好不好,得看用在哪里。也许对于MNIST这个28*28的数据集并不需要池化也能work,但如果是1000*1000的大图呢?越远的东西就越看不清,这难道不是池化的结果?
所以我认为池化也是可取的,不过池化应该对低层的特征进行,高层的信息池化可能就会有问题了,尤其是CNN的最后一层,已有的模型一般都是用Global Pooling(如我的实验模型所示),这会极大地降低特征的迁移能力(比如实验中单数字模型能不能直接用来测试多数字)。退一步讲,如果坚决不用池化,那我用stride=2的卷积,不跟stride=1的卷积后接一个大小为2的池化是类似的吗?笔者前面的Capsule实验中,也将池化跟Capsule配合使用了,效果也没有变糟。
结语 #
这应该是到目前为止我写的最长的单篇博客了~不知道大家对这个Capsule饭局满不满意呢?
最后不得不吐槽一下,Hinton真会起名字,把神经网络重新叫做深度学习,然后深度学习就火了,现在把聚类的迭代算法放到神经网络中,称之为做动态路由,不知道会不会再次重现深度学习的辉煌呢?(笑,闪~)
转载到请包括本文地址:https://kexue.fm/archives/4819
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Jan. 23, 2018). 《揭开迷雾,来一顿美味的Capsule盛宴 》[Blog post]. Retrieved from https://kexue.fm/archives/4819
@online{kexuefm-4819,
title={揭开迷雾,来一顿美味的Capsule盛宴},
author={苏剑林},
year={2018},
month={Jan},
url={\url{https://kexue.fm/archives/4819}},
}











July 9th, 2019
[...]揭开迷雾,来一顿美味的Capsule盛宴再来一顿贺岁宴:从K-Means到Capsule[...]
July 12th, 2019
今天看了Hinton6月份的新作Stacked Capsule Autoencoders,做的实验依旧是以MNIST为主,其聚类的准确率应该是达到了目前最高水准98.9%,SVHN也还行,毕竟是聚类,但是cifar10的结果最好的也只有跟普通的AE差不多,像MNIST和SVHN都是数字,cifar10是一些自然图像,感觉确认如博主所说Capsule还没有在一些复杂背景图像上取得好的效果,这可能也是其没有广泛应用的原因。arxiv地址:https://arxiv.org/pdf/1906.06818.pdf
July 12th, 2019
感觉hinton在自己挖坑自己填。。。
August 27th, 2019
大佬请教一下,从Conv1到PrimaryCaps之间的卷积结构是什么样的,是8组参数独立的32channels的9*9卷积吗,然后每个卷积里面有256个filters吗?那参数也太多了,9x9x256x32x8,500万个参数
按图示来说确实是这样。
标准的capsule参数量确实会比普通的神经网络多一个数量级左右。
hinton的论文里说Routing=3时能跑出来99.75%的准确率,但是我自己运行死活出不来这么高的准确率啊,99.50就到头了还不如基准模型,大神您跑这个程序的时候出过他说的这个结果吗
我好像跑出过99.6%吧,他那个99.75%还包括重构部分吧
August 31st, 2019
大神你好!
”假如经过无穷多次迭代(实际上算力有限,做不到,但理论上总可以做到的),那么r→∞,这样的话softmax的结果是非零即1,也就是说,每个底层的胶囊仅仅联系到唯一一个上层胶囊。“
我个人认为hinton的方案更加合理一些。他的b = b+内积的方式感觉更像是一个加入了动量的迭代。c_ij倾向于独热我认为在这个情景下是没问题的。
另外关于动态路由迭代的次数k,我实验中发现大于3的情况也并无不可, 只要每层设置的胶囊个数足够多(通常不少胶囊$\sum_i c_{ij}$都很小,即作用很小,最后去掉也可以)
不足之处还请指正!谢谢!
“他的b = b+内积的方式感觉更像是一个加入了动量的迭代。c_ij倾向于独热我认为在这个情景下是没问题的。”
这段话没有为你的
“我个人认为hinton的方案更加合理一些”
这句话提供任何理论上或者直觉上的支持。
实验里也发现这样做收敛更快。如果不加入动量的话有反复震荡的情况发生(我不知道这样解释可不可以)
你是直接拿优化器的结论来类比?这具有类比性么?
September 25th, 2019
您好,很抱歉打扰您,想请问一下为什么您在代码中重写了自己的$softmax$函数呢,是因为您在实验中发现数值会溢出吗?还有$squash$为什么您加了一个$\epsilon$呢,个人感觉没必要呀。。
重新定义softmax是因为当时keras的softmax不支持axis参数,后面我提出他们才加上的。
September 25th, 2019
还有一点小疑惑,为什么您共享时的实现使用的是卷积呢?我试了试直接使用全连接层实现也可以?前者有什么优势吗。谢谢苏神指导!
为了跟不共享的时候格式一致罢了,不共享时用的是local_conv1d,共享时就用conv1d。
December 3rd, 2019
大神您好,我琢磨了很久您对于capsule的聚类理解,我还是没搞懂。您文中说了,上层capsule是低层capsule的某种聚类结果,那么究竟是在聚类什么?为什么低阶层的特征向量聚类之后得到的聚类中心是高阶层的特征向量?或者我理解就是比如人脸为高阶特征,眼睛、嘴巴、鼻子等是低阶特征,那么为什么眼睛、嘴巴、鼻子聚类之后的聚类中心就是人脸特征?谢谢
眼睛、嘴巴、鼻子等组成的“整个类”可以作为人脸表征,这个应该没意见吧?而在很多类的情况下,类中心可以作为类的表征。所以聚类中心可以作为人脸表征。
January 6th, 2020
博主好,感觉你的文章写得特别好呀,易懂。
我感觉有些问题我有点不是很理解,
1.不太理解胶囊的含义,感觉就是向量打包成胶囊。
2. 对于vector in vector out 和scalar in scalar out, 感觉主要原因是激活函数 (dynamic routing 确实是处理向量), 觉得也可以考虑在CNN使用Squash函数,那么照文章所说,CNN输出squash激活后的也算是向量。
3. 觉得第2点可行的话,第1点感觉不到胶囊存在的意义。
有dynamic routing的过程才叫胶囊,而不是因为squash。
March 19th, 2020
想问下大佬动态路由中每次迭代计算vj的时候squash是必须的吗?感觉迭代完r次之后最后输出v的时候再做squash也可以。
可以是可以,但是不能自圆其说。