生成扩散模型漫谈(二):DDPM = 自回归式VAE
By 苏剑林 | 2022-07-06 | 237128位读者 | 引用在文章《生成扩散模型漫谈(一):DDPM = 拆楼 + 建楼》中,我们为生成扩散模型DDPM构建了“拆楼-建楼”的通俗类比,并且借助该类比完整地推导了生成扩散模型DDPM的理论形式。在该文章中,我们还指出DDPM本质上已经不是传统的扩散模型了,它更多的是一个变分自编码器VAE,实际上DDPM的原论文中也是将它按照VAE的思路进行推导的。
所以,本文就从VAE的角度来重新介绍一版DDPM,同时分享一下自己的Keras实现代码和实践经验。
Github地址:https://github.com/bojone/Keras-DDPM
多步突破
在传统的VAE中,编码过程和生成过程都是一步到位的:
\begin{equation}\text{编码:}\,\,x\to z\,,\quad \text{生成:}\,\,z\to x\end{equation}
变分自编码器(八):估计样本概率密度
By 苏剑林 | 2021-12-09 | 102414位读者 | 引用在本系列的前面几篇文章中,我们已经从多个角度来理解了VAE,一般来说,用VAE是为了得到一个生成模型,或者是做更好的编码模型,这都是VAE的常规用途。但除了这些常规应用外,还有一些“小众需求”,比如用来估计$x$的概率密度,这在做压缩的时候通常会用到。
本文就从估计概率密度的角度来了解和推导一下VAE模型。
两个问题
所谓估计概率密度,就是在已知样本$x_1,x_2,\cdots,x_N\sim \tilde{p}(x)$的情况下,用一个待定的概率密度簇$q_{\theta}(x)$去拟合这批样本,拟合的目标一般是最小化负对数似然:
\begin{equation}\mathbb{E}_{x\sim \tilde{p}(x)}[-\log q_{\theta}(x)] = -\frac{1}{N}\sum_{i=1}^N \log q_{\theta}(x_i)\label{eq:mle}\end{equation}
UniVAE:基于Transformer的单模型、多尺度的VAE模型
By 苏剑林 | 2021-06-29 | 106560位读者 | 引用变分自编码器(七):球面上的VAE(vMF-VAE)
By 苏剑林 | 2021-05-17 | 212707位读者 | 引用在《变分自编码器(五):VAE + BN = 更好的VAE》中,我们讲到了NLP中训练VAE时常见的KL散度消失现象,并且提到了通过BN来使得KL散度项有一个正的下界,从而保证KL散度项不会消失。事实上,早在2018年的时候,就有类似思想的工作就被提出了,它们是通过在VAE中改用新的先验分布和后验分布,来使得KL散度项有一个正的下界。
该思路出现在2018年的两篇相近的论文中,分别是《Hyperspherical Variational Auto-Encoders》和《Spherical Latent Spaces for Stable Variational Autoencoders》,它们都是用定义在超球面的von Mises–Fisher(vMF)分布来构建先后验分布。某种程度上来说,该分布比我们常用的高斯分布还更简单和有趣~
KL散度消失
我们知道,VAE的训练目标是
\begin{equation}\mathcal{L} = \mathbb{E}_{x\sim \tilde{p}(x)} \Big[\mathbb{E}_{z\sim p(z|x)}\big[-\log q(x|z)\big]+KL\big(p(z|x)\big\Vert q(z)\big)\Big]
\end{equation}
变分自编码器(六):从几何视角来理解VAE的尝试
By 苏剑林 | 2020-09-10 | 108730位读者 | 引用前段时间公司组织技术分享,轮到笔者时,大家希望我讲讲VAE。鉴于之前笔者也写过变分自编码器系列,所以对笔者来说应该也不是特别难的事情,因此就答应了下来,后来仔细一想才觉得犯难:怎么讲才好呢?
对于VAE来说,之前笔者有两篇比较系统的介绍:《变分自编码器(一):原来是这么一回事》和《变分自编码器(二):从贝叶斯观点出发》。后者是纯概率推导,对于不做理论研究的人来说其实没什么意义,也不一定能看得懂;前者虽然显浅一点,但也不妥,因为它是从生成模型的角度来讲的,并没有说清楚“为什么需要VAE”(说白了,VAE可以带来生成模型,但是VAE并不一定就为了生成模型),整体风格也不是特别友好。
笔者想了想,对于大多数不了解但是想用VAE的读者来说,他们应该只希望大概了解VAE的形式,然后想要知道“VAE有什么作用”、“VAE相比AE有什么区别”、“什么场景下需要VAE”等问题的答案,对于这种需求,上面两篇文章都无法很好地满足。于是笔者尝试构思了VAE的一种几何图景,试图从几何角度来描绘VAE的关键特性,在此也跟大家分享一下。
强大的NVAE:以后再也不能说VAE生成的图像模糊了
By 苏剑林 | 2020-07-10 | 177427位读者 | 引用昨天早上,笔者在日常刷arixv的时候,然后被一篇新出来的论文震惊了!论文名字叫做《NVAE: A Deep Hierarchical Variational Autoencoder》,顾名思义是做VAE的改进工作的,提出了一个叫NVAE的新模型。说实话,笔者点进去的时候是不抱什么希望的,因为笔者也算是对VAE有一定的了解,觉得VAE在生成模型方面的能力终究是有限的。结果,论文打开了,呈现出来的画风是这样的:
然后笔者的第一感觉是这样的:
W!T!F! 这真的是VAE生成的效果?这还是我认识的VAE么?看来我对VAE的认识还是太肤浅了啊,以后再也不能说VAE生成的图像模糊了...
变分自编码器(五):VAE + BN = 更好的VAE
By 苏剑林 | 2020-05-06 | 306540位读者 | 引用本文我们继续之前的变分自编码器系列,分析一下如何防止NLP中的VAE模型出现“KL散度消失(KL Vanishing)”现象。本文受到参考文献是ACL 2020的论文《A Batch Normalized Inference Network Keeps the KL Vanishing Away》的启发,并自行做了进一步的完善。
值得一提的是,本文最后得到的方案还是颇为简洁的——只需往编码输出加入BN(Batch Normalization),然后加个简单的scale——但确实很有效,因此值得正在研究相关问题的读者一试。同时,相关结论也适用于一般的VAE模型(包括CV的),如果按照笔者的看法,它甚至可以作为VAE模型的“标配”。
最后,要提醒读者这算是一篇VAE的进阶论文,所以请读者对VAE有一定了解后再来阅读本文。
VAE简单回顾
这里我们简单回顾一下VAE模型,并且讨论一下VAE在NLP中所遇到的困难。关于VAE的更详细介绍,请读者参考笔者的旧作《变分自编码器(一):原来是这么一回事》、《变分自编码器(二):从贝叶斯观点出发》等。
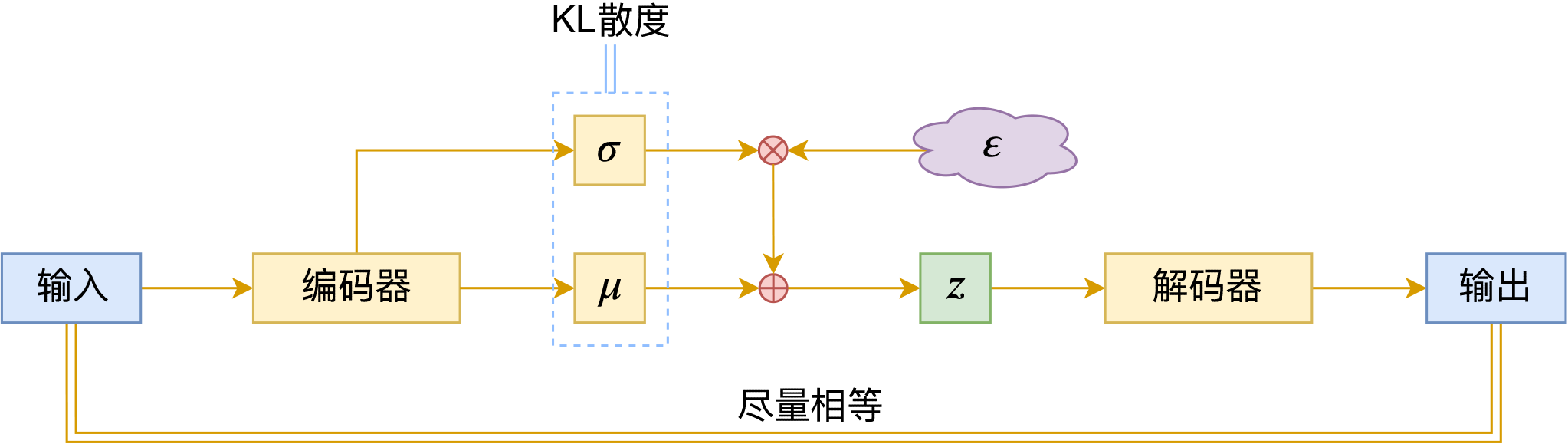
VAE的训练流程
VAE的训练流程大概可以图示为
从变分编码、信息瓶颈到正态分布:论遗忘的重要性
By 苏剑林 | 2018-11-27 | 230534位读者 | 引用这是一篇“散文”,我们来谈一下有着千丝万缕联系的三个东西:变分自编码器、信息瓶颈、正态分布。
众所周知,变分自编码器是一个很经典的生成模型,但实际上它有着超越生成模型的含义;而对于信息瓶颈,大家也许相对陌生一些,然而事实上信息瓶颈在去年也热闹了一阵子;至于正态分布,那就不用说了,它几乎跟所有机器学习领域都有或多或少的联系。
那么,当它们三个碰撞在一块时,又有什么样的故事可说呢?它们跟“遗忘”又有什么关系呢?
变分自编码器
在本博客你可以搜索到若干几篇介绍VAE的文章。下面简单回顾一下。
理论形式回顾
简单来说,VAE的优化目标是:
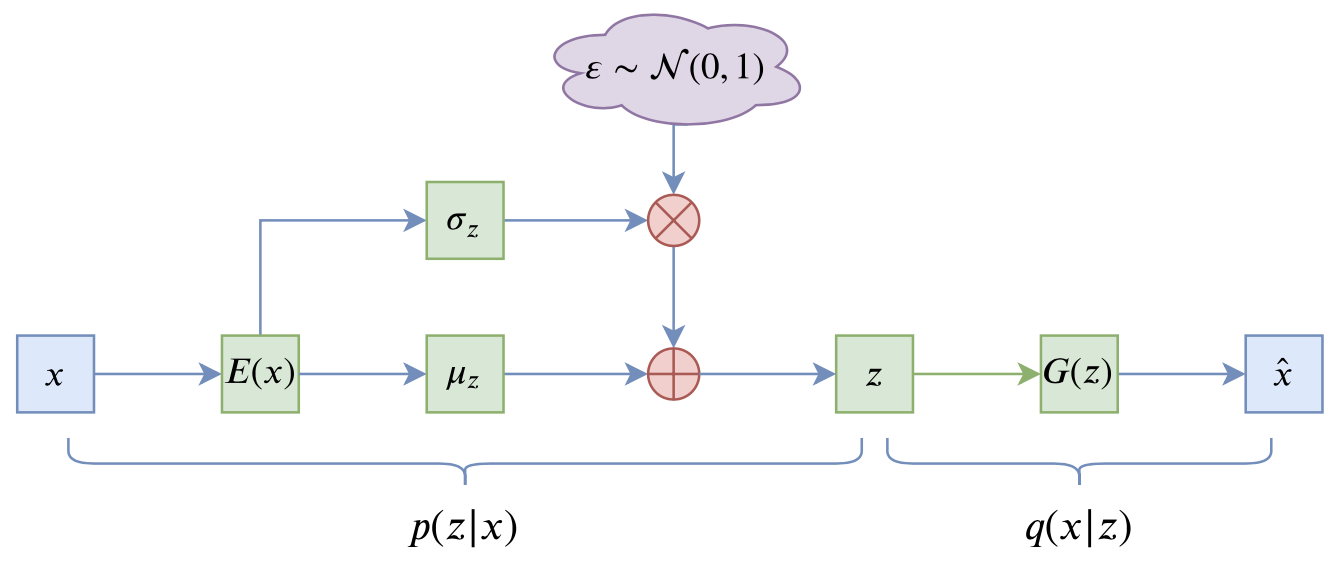
\begin{equation}KL(\tilde{p}(x)p(z|x)\Vert q(z)q(x|z))=\iint \tilde{p}(x)p(z|x)\log \frac{\tilde{p}(x)p(z|x)}{q(x|z)q(z)} dzdx\end{equation}
其中$q(z)$是标准正态分布,$p(z|x),q(x|z)$是条件正态分布,分别对应编码器、解码器。具体细节可以参考《变分自编码器(二):从贝叶斯观点出发》。









最近评论