【翻译】星空之夜:夏季恒星的色彩
By 苏剑林 | 2013-07-25 | 40231位读者 | 引用施密特系统的校正镜方程求解
By 苏剑林 | 2011-02-11 | 41031位读者 | 引用非抛物面望远镜的校正镜方程求解
The Corrector Plate of Non-parabola Telescope
本文在牧夫天文论坛的讨论:
http://www.astronomy.ac/bbs/thread-160257-1-1.html
为了克服折射望远镜的色差问题,1670年,牛顿制造了第一台实用的反射式望远镜,将望远镜的主镜由玻璃透镜换成了抛物反射面,从而消除了色差。然而,相比球面镜,大口径的抛物面并不容易磨制。因为制作大球面镜只需要将曲率相等的小镜片相对自由组合在一起就行了,而抛物线每点的曲率并不相等,所以需要逐个磨制曲率不等的小镜片,并按照严格的顺序组合起来。这无疑大大增加了磨制难度。
为了解决这一难题,天文学家们想到了一个折衷的办法:以球面为主镜,并配以校正镜来校正球差。迎着这一思路,施密特望远镜随之而生。而当代的大望远镜基本上都是沿用这一思路。然而,校正镜是一个比抛物面更加复杂的四次曲面,磨制工艺要求更高,因此,校正镜也不宜过大。
《自然极值》系列——6.最速降线的解答
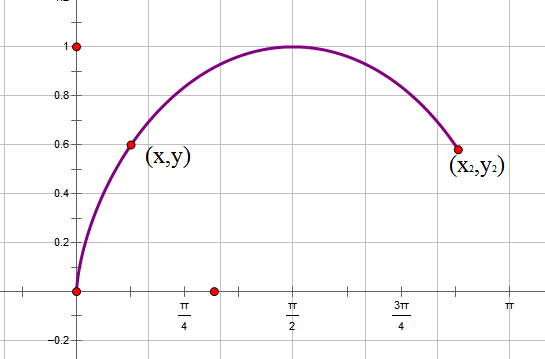
By 苏剑林 | 2010-12-10 | 80237位读者 | 引用通过上一小节的小故事,我们已经能够基本了解最速降线的内容了,它就是要我们求出满足某一极值条件的一个未知函数,由于函数是未知的,因此这类问题被称为“泛分析”。其中还谈到,伯努利利用费马原理巧妙地得出了答案,那么我们现在就再次回顾历史,追寻伯努利的答案,并且寻找进一步的应用。
为了计算方便,我们把最速降线倒过来,把初始点设置在原点。在下落过程中,重力势能转化为动能,因此,在点(x,y)处有$\frac{1}{2} mv^2=mgy\Rightarrow v=\sqrt{2gy}$,由于纯粹为了探讨曲线形状,所以我们使g=0.5,即$v=\sqrt{y}$。在点(x,y)处所走的路程为$ds=\sqrt{dy^2+dx^2}=\sqrt{\dot{y}^2+1}dx$,所以时间为$dt=\frac{ds}{v}=\frac{\sqrt{\dot{y}^2+1}dx}{\sqrt{y}}$,于是最速降线问题就是求使$t=\int_0^{x_2} \frac{\sqrt{\dot{y}^2+1}dx}{\sqrt{y}}$最小的函数。
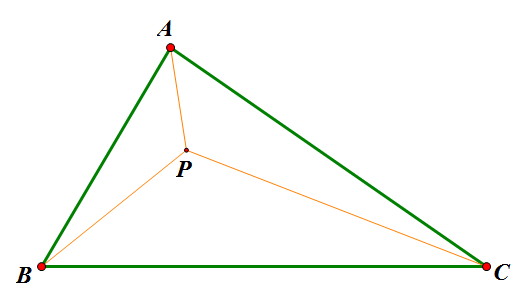
《自然极值》系列——4.费马点问题
By 苏剑林 | 2010-11-28 | 113025位读者 | 引用通过上面众多的文字描述,也许你还不大了解这两个原理有何美妙之处,也或者你已经迫不及待地想去应用它们却不知思路。为了不至于让大家产生“审美疲劳”,接下来我们将试图利用这两个原理对费马点问题进行探讨,看看原理究竟是怎么发挥作用的。运用的关键在于:如何通过适当的变换将其与光学或势能联系起来。
传统费马点问题是指在ΔABC中寻找点P,使得$AP+BP+CP$最小的问题;而广义的费马点则改成使$k_1 AP+k_2 BP+k_3 CP$最小。这是很具有现实意义的,是“在三个村庄之间建立一个中转站,如何才能使运送成为最低”之类的最优问题。我们将从光学和势能两个角度对这个问题进行探讨(也许有的读者已经阅读过了利用重力的原理来求解费马点,但是我想光学的方法依然会是你眼前一亮的。)
《自然极值》系列——2.费马原理
By 苏剑林 | 2010-11-27 | 57327位读者 | 引用物理学的美不仅仅表现在简洁的公式上。我们还惊奇地发现,很多物理现象都是按照使某个变量达到极值的方式发生。一个典型的例子就是费马原理,它指出了光的传播路径的一个重要规律:光总是沿着所花时间最短的路径传播。这里我们将简单介绍一下费马原理。
费马原理俗称“最快到达原理”、“最小时间原理”。1657年,费马提出:
从P点到达Q点,在所有可行的路径中,光选择了所需时间最短的一条。
从P点到达Q点,在所有可行的路径中,光选择了所需时间为极值的一条。
这是一个极其奇妙的原理,也是自然界中最神奇的极值之一。作为非生物的光,居然自主地选择了最优路径,成为世界上“效率最高”的东西,这让人不得不佩服宇宙的伟大。这究竟是造物者的精心设计,还是无心之作?











最近评论