科学空间|Scientific Spaces

流年

《量子力学与路径积分》的习题解答终于艰难地推进到了0.4版本，目前已经基本完成了前7章的习题。

今天已经是2016年1月9号了，2015年已经远去，都忘记跟大家说一声新年快乐了，实在抱歉。在这里补充一句：祝大家新年快乐，事事如意！。

笔者已经大四了，现在是临近期末考，又临近毕业。最近忙的事情有很多，其中之一是我加入了一个互联网小公司的创业队伍中，负责文本挖掘，偶尔也写写爬虫，等等，感觉自己进去之后，增长了不少见识，也增加了不少技术知识，较之我上一次实习，又有不一样的高度。现在里边有好几样事情排队着做，可谓忙得不亦悦乎了。还有，我也开始写毕业论文了，早点写完能够多点时间，学学自己喜欢的东西，毕业论文我写的是路径积分相关的内容，自我感觉写得还是比较清楚易懂的，等时机成熟了，发出来，向大家普及路径积分^_^。此外，每天做点路径积分的习题，也要消耗不少时间，有些比较难的题目，基本一道就做几个早上才能写出比较满意的答案。总感觉想学的想做的事情有很多，可是时间很少。

点击阅读全文...

习题解答继续艰难推进中，目前是0.5版本，相比0.4版，跳过了8、9章，先做了第10、11章统计力学部分的习题。

第10章有10道习题，第11章其实没有习题。看上去很少，但其实每一道习题的难度都很大。这两章的主要内容都是在用路径积分方法算统计力学中的配分函数，这本来就是一个很艰辛的课题。加上费曼在书中那形象的描述，容易让读者能够认识到大概，但是却很难算下去。事实上，这一章的习题，我参考了相当多的资料，中文的、英文的都有，才勉强完成了。

虽说是完成，但10道题目中，我只完成了9道，其中问题10-3是有困惑的，我感觉的结果跟费曼给出的不一样，因此就算不下去了。在这里提出来，希望了解的读者赐教。

点击阅读全文...

上一篇博文的发布时间是4月15日，到今天刚好一个月没更新了，但是科学空间的访问量还在。感谢大家对本空间的支持，BoJone对久未更新表示非常抱歉。在恢复更新之前，请允许笔者记记流水账。

在“消失”的一个月中，笔者主要的事情是毕业论文和数据挖掘竞赛。首先毕业论文方面，论文于4月22日交稿，4月29日答辩，答辩完后就意味着毕业论文的事情结束了。我的毕业论文主要写了路径积分在描述随机游走、偏微分方程、随机微分方程的应用。既然是本科论文，就不能说得太晦涩，因此论文整体来看还是比较易读的，可以作为路径积分的入门教程。后面我会略加修改，分开几部分发布在科学空间中的，到时请大家批评指正。

说到路径积分，不得不说到做《量子力学与路径积分》的习题解答这件事情了。很遗憾，这一个多月来，基本没有时间做习题。不过后面我会继续做下去的，已发布的版本，也请有兴趣的读者指出问题。记得年初的时候，朋友问我今年的愿望是什么，我随意地回答了“希望做完一本书的习题”，这本书，当然就是《量子力学与路径积分》了，我相信今年应该能够完成的。

点击阅读全文...

路径积分是量子力学的一种描述方法，源于物理学家费曼[5]，它是一种泛函积分，它已经成为现代量子理论的主流形式. 近年来，研究人员对它的兴趣愈发增加，尤其是它在量子领域以外的应用，出现了一些著作，如[7]. 但在国内了解路径积分的人并不多，很多量子物理专业的学生可能并没有听说过路径积分.

从数学角度来看，路径积分是求偏微分方程的Green函数的一种方法. 我们知道，在偏微分方程的研究中，如果能够求出对应的Green函数，那么对偏微分方程的研究会大有帮助，而通常情况下Green函数并不容易求解. 但构建路径积分只需要无穷小时刻的Green函数，因此形式和概念上都相当简单.

本章并没有新的内容，只是做了一个尝试：从随机游走问题出发，给出路径积分的一个简明而直接的介绍，展示了如何将抛物型的偏微分方程问题转化为路径积分形式.

从点的概率到路径的概率

在上一章对随机游走的研究中，我们得出从$x_0$出发，$t$时间后，走到$x_n$处的概率密度为
$$\frac{1}{\sqrt{2\pi \alpha T}}\exp\left(-\frac{(x_n-x_0)^2}{2\alpha t}\right).\tag{22}$$
这是某时刻某点到另一个时刻另一点的概率，在数学上，我们称之为扩散方程$(21)$的传播子，或者Green函数.

点击阅读全文...

路径积分方法为解决某些随机问题带来了新视角.

一个例子：股票价格模型

考虑有风险资产(如股票)，在$t$时刻其价格为$S_t$，考虑的时间区间为$[0,T]$，0表示初始时间，$T$表示为到期日. $S_t$看作是随时间变化的连续时间变量，并服从下列随机微分方程:
$$dS_t^0=rS_t^0 dt;\quad dS_t=S_t(\mu dt+\sigma dW_t).\tag{70}$$
其中，$\mu$和$\sigma$是两个常量，$W_t$是一个标准布朗运动.

关于$S_t$的方程是一个随机微分方程，一般解决思路是通过随机微积分. 随机微积分有别于一般的微积分的地方在于，随机微积分在做一阶展开的时候，不能忽略$dS_t^2$项，因为$dW_t^2=dt$. 比如，设$S_t=e^{x_t}$，则$x_t=\ln S_t$
$$\begin{aligned}dx_t=&\ln(S_t+dS_t)-\ln S_t=\frac{dS_t}{S_t}-\frac{dS_t^2}{2S_t^2}\\
=&\frac{S_t(\mu dt+\sigma dW_t)}{S_t}-\frac{[S_t(\mu dt+\sigma dW_t)]^2}{2S_t^2}\\
=&\mu dt+\sigma dW_t-\frac{1}{2}\sigma^2 dW_t^2\quad(\text{其余项均低于}dt\text{阶})\\
=&\left(\mu-\frac{1}{2}\sigma^2\right) dt+\sigma dW_t\end{aligned}
,\tag{71}$$

点击阅读全文...

写在前面：前面的博文已经提过，在上个月我参加了第四届泰迪杯数据挖掘竞赛，做的是A题，跟OCR系统有些联系，还承诺过会把最终的结果开源。最近忙于毕业、搬东西，一直没空整理这些内容，现在抽空整理一下。

把结果发出来，并不是因为结果有多厉害、多先进（相反，当我对比了百度的这篇论文《基于深度学习的图像识别进展：百度的若干实践》之后，才发现论文的内容本质上还是传统那一套，远远还跟不上时代的潮流），而是因为虽然OCR技术可以说比较成熟了，但网络上根本就没有对OCR系统进行较为详细讲解的文章，而本文就权当补充这部分内容吧。我一直认为，技术应该要开源才能得到发展（当然，在中国这一点也确实值得商榷，因为开源很容易造成山寨），不管是数学物理研究还是数据挖掘，我大多数都会发表到博客中，与大家交流。

点击阅读全文...

研究背景

关于光学字符识别(Optical Character Recognition, 下面都简称OCR)，是指将图像上的文字转化为计算机可编辑的文字内容，众多的研究人员对相关的技术研究已久，也有不少成熟的OCR技术和产品产生，比如汉王OCR、ABBYY FineReader、Tesseract OCR等. 值得一提的是，ABBYY FineReader不仅正确率高(包括对中文的识别)，而且还能保留大部分的排版效果，是一个非常强大的OCR商业软件.

然而，在诸多的OCR成品中，除了Tesseract OCR外，其他的都是闭源的、甚至是商业的软件，我们既无法将它们嵌入到我们自己的程序中，也无法对其进行改进. 开源的唯一选择是Google的Tesseract OCR，但它的识别效果不算很好，而且中文识别正确率偏低，有待进一步改进.

综上所述，不管是为了学术研究还是实际应用，都有必要对OCR技术进行探究和改进. 我们队伍将完整的OCR系统分为“特征提取”、“文字定位”、“光学识别”、“语言模型”四个方面，逐步进行解决，最终完成了一个可用的、完整的、用于印刷文字的OCR系统. 该系统可以初步用于电商、微信等平台的图片文字识别，以判断上面信息的真伪.

研究假设

在本文中，我们假设图像的文字部分有以下的特征：

点击阅读全文...

经过第一部分，我们已经较好地提取了图像的文本特征，下面进行文字定位. 主要过程分两步：1、邻近搜索，目的是圈出单行文字；2、文本切割，目的是将单行文本切割为单字.

邻近搜索

我们可以对提取的特征图进行连通区域搜索，得到的每个连通区域视为一个汉字. 这对于大多数汉字来说是适用，但是对于一些比较简单的汉字却不适用，比如“小”、“旦”、“八”、“元”这些字，由于不具有连通性，所以就被分拆开了，如图13. 因此，我们需要通过邻近搜索算法，来整合可能成字的区域，得到单行的文本区域.

图13 直接搜索连通区域，会把诸如“元”之类的字分拆开

邻近搜索的目的是进行膨胀，以把可能成字的区域“粘合”起来. 如果不进行搜索就膨胀，那么膨胀是各个方向同时进行的，这样有可能把上下行都粘合起来了. 因此，我们只允许区域向单一的一个方向膨胀. 我们正是要通过搜索邻近区域来确定膨胀方向(上、下、左、右)：

邻近搜索* 从一个连通区域出发，可以找到该连通区域的水平外切矩形，将连通区域扩展到整个矩形. 当该区域与最邻近区域的距离小于一定范围时，考虑这个矩形的膨胀，膨胀的方向是最邻近区域的所在方向.

既然涉及到了邻近，那么就需要有距离的概念. 下面给出一个比较合理的距离的定义.

距离

图14 两个示例区域

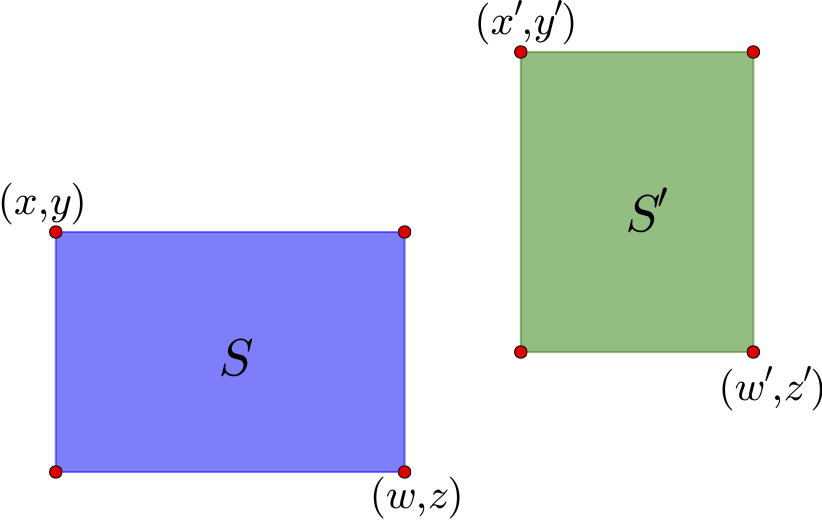
如上图，通过左上角坐标$(x,y)$和右下角坐标$(z,w)$就可以确定一个矩形区域，这里的坐标是以左上角为原点来算的. 这个区域的中心是$\left(\frac{x+w}{2},\frac{y+z}{2}\right)$. 对于图中的两个区域$S$和$S'$，可以计算它们的中心向量差
$$(x_c,y_c)=\left(\frac{x'+w'}{2}-\frac{x+w}{2},\frac{y'+z'}{2}-\frac{y+z}{2}\right)\tag{10}$$
如果直接使用$\sqrt{x_c^2+y_c^2}$作为距离是不合理的，因为这里的邻近应该是按边界来算，而不是中心点. 因此，需要减去区域的长度：
$$(x'_c,y'_c)=\left(x_c-\frac{w-x}{2}-\frac{w'-x'}{2},y_c-\frac{z-y}{2}-\frac{z'-y'}{2}\right)\tag{11}$$
距离定义为
$$d(S,S')=\sqrt{[\max(x'_c,0)]^2+[\max(y'_c,0)]^2}\tag{12}$$
至于方向，由$(x_c,y_c)$的幅角进行判断即可.

然而，按照前面的“邻近搜索*”方法，容易把上下两行文字粘合起来，因此，基于我们的横向排版假设，更好的方法是只允许横向膨胀：

邻近搜索 从一个连通区域出发，可以找到该连通区域的水平外切矩形，将连通区域扩展到整个矩形. 当该区域与最邻近区域的距离小于一定范围时，考虑这个矩形的膨胀，膨胀的方向是最邻近区域的所在方向，当且仅当所在方向是水平的，才执行膨胀操作.

结果

有了距离之后，我们就可以计算每两个连通区域之间的距离，然后找出最邻近的区域. 我们将每个区域向它最邻近的区域所在的方向扩大4分之一，这样邻近的区域就有可能融合为一个新的区域，从而把碎片整合.

实验表明，邻近搜索的思路能够有效地整合文字碎片，结果如图15.

图15 通过邻近搜索后，圈出的文字区域