科学空间|Scientific Spaces

最近有需求要爬一些儿童故事类的语料用来训练词向量，因此找了一些童话故事网把整站的童话文章爬了下来。下面分享一下用Python实现的这个过程，并把之前爬取百度百科的经验，结合着分享出来。本教程适合于以下需求：需要遍历爬取指定的网站、并且指定网站没有反爬虫措施。在这种前提之下，所考验我们的仅仅是遍历算法和编程技巧了。

假设

再次表明我们的假设：

1、需要遍历整个网站来爬取我们需要的信息；

2、网站没有反爬虫措施；

3、网站的所有页面，总可以通过网站首页，逐步点击超链接来到达。

点击阅读全文...

警告

以下内容包含诸多高危动作，请勿随意模仿。未成年人请在父母的陪同下观看～(^_^）

自杀式

Linux系统（下面内容同时适用于Mac OS）以开源自由闻名，然而有些时候它也开放过头了，而笔者也被它无比开发的特性坑了好几次（当然，主要是笔者使用习惯不好），遂总结分享，供大家娱乐。

最经典的例子就是，通过以下命令就可以实现“自杀”：

sudo rm / -rf

这就把你的Linux系统给毁了。显然，如果是在Windows中，这相当于在操作系统中格式化系统盘，这是绝对不允许的。

点击阅读全文...

如果问我哪个是最方便、最好用的词向量模型，我觉得应该是word2vec，但如果问我哪个是最漂亮的词向量模型，我不知道，我觉得各个模型总有一些不足的地方。且不说试验效果好不好（这不过是评测指标的问题），就单看理论也没有一个模型称得上漂亮的。

本文讨论了一些大家比较关心的词向量的问题，很多结论基本上都是实验发现的，缺乏合理的解释，包括：

如果去构造一个词向量模型？

为什么用余弦值来做近义词搜索？向量的内积又是什么含义？

词向量的模长有什么特殊的含义？

为什么词向量具有词类比性质？（国王-男人+女人=女王）

得到词向量后怎么构建句向量？词向量求和作为简单的句向量的依据是什么？

这些讨论既有其针对性，也有它的一般性，有些解释也许可以直接迁移到对glove模型和skip gram模型的词向量性质的诠释中，读者可以自行尝试。

围绕着这些问题的讨论，本文提出了一个新的类似glove的词向量模型，这里称之为simpler glove，并基于斯坦福的glove源码进行修改，给出了本文的实现，具体代码在Github上。

点击阅读全文...

从条件概率到互信息

目前，词向量模型的原理基本都是词的上下文的分布可以揭示这个词的语义，就好比“看看你跟什么样的人交往，就知道你是什么样的人”，所以词向量模型的核心就是对上下文的关系进行建模。除了glove之外，几乎所有词向量模型都是在对条件概率$P(w|context)$进行建模，比如Word2Vec的skip gram模型就是对条件概率$P(w_2|w_1)$进行建模。但这个量其实是有些缺点的，首先它是不对称的，即$P(w_2|w_1)$不一定等于$P(w_1|w_2)$，这样我们在建模的时候，就要把上下文向量和目标向量区分开，它们不能在同一向量空间中；其次，它是有界的、归一化的量，这就意味着我们必须使用softmax等方法将它压缩归一，这造成了优化上的困难。

事实上，在NLP的世界里，有一个更加对称的量比单纯的$P(w_2|w_1)$更为重要，那就是
\[\frac{P(w_1,w_2)}{P(w_1)P(w_2)}=\frac{P(w_2|w_1)}{P(w_2)}\tag{1}\]
这个量的大概意思是“两个词真实碰面的概率是它们随机相遇的概率的多少倍”，如果它远远大于1，那么表明它们倾向于共同出现而不是随机组合的，当然如果它远远小于1，那就意味着它们俩是刻意回避对方的。这个量在NLP界是举足轻重的，我们暂且称它为“相关度“，当然，它的对数值更加出名，大名为点互信息（Pointwise Mutual Information，PMI）：
\[\text{PMI}(w_1,w_2)=\log \frac{P(w_1,w_2)}{P(w_1)P(w_2)}\tag{2}\]

有了上面的理论基础，我们认为，如果能直接对相关度进行建模，会比直接对条件概率$P(w_2|w_1)$建模更加合理，所以本文就围绕这个角度进行展开。在此之前，我们先进一步展示一下互信息本身的美妙性质。

点击阅读全文...

最后，我们来看一下词向量模型$(15)$会有什么好的性质，或者说，如此煞费苦心去构造一个新的词向量模型，会得到什么回报呢？

模长的含义

似乎所有的词向量模型中，都很少会关心词向量的模长。有趣的是，我们上述词向量模型得到的词向量，其模长还能在一定程度上代表着词的重要程度。我们可以从两个角度理解这个事实。

在一个窗口内的上下文，中心词重复出现概率其实是不大的，是一个比较随机的事件，因此可以粗略地认为
\[P(w,w) \sim P(w)\tag{24}\]
所以根据我们的模型，就有
\[e^{\langle\boldsymbol{v}_{w},\boldsymbol{v}_{w}\rangle} =\frac{P(w,w)}{P(w)P(w)}\sim \frac{1}{P(w)}\tag{25}\]
所以
\[\Vert\boldsymbol{v}_{w}\Vert^2 \sim -\log P(w)\tag{26}\]
可见，词语越高频（越有可能就是停用词、虚词等），对应的词向量模长就越小，这就表明了这种词向量的模长确实可以代表词的重要性。事实上，$-\log P(w)$这个量类似IDF，有个专门的名称叫ICF，请参考论文《TF-ICF: A New Term Weighting Scheme for Clustering Dynamic Data Streams》。

点击阅读全文...

损失函数

现在，我们来定义loss，以便把各个词向量求解出来。用$\tilde{P}$表示$P$的频率估计值，那么我们可以直接以下式为loss
\[\sum_{w_i,w_j}\left(\langle \boldsymbol{v}_i, \boldsymbol{v}_j\rangle-\log\frac{\tilde{P}(w_i,w_j)}{\tilde{P}(w_i)\tilde{P}(w_j)}\right)^2\tag{16}\]
相比之下，无论在参数量还是模型形式上，这个做法都比glove要简单，因此称之为simpler glove。glove模型是
\[\sum_{w_i,w_j}\left(\langle \boldsymbol{v}_i, \boldsymbol{\hat{v}}_j\rangle+b_i+\hat{b}_j-\log X_{ij}\right)^2\tag{17}\]
在glove模型中，对中心词向量和上下文向量做了区分，然后最后模型建议输出的是两套词向量的求和，据说这效果会更好，这是一个比较勉强的trick，但也不是什么毛病。最大的问题是参数$b_i,\hat{b}_j$也是可训练的，这使得模型是严重不适定的！我们有
\[\begin{aligned}&\sum_{w_i,w_j}\left(\langle \boldsymbol{v}_i, \boldsymbol{\hat{v}}_j\rangle+b_i+\hat{b}_j-\log \tilde{P}(w_i,w_j)\right)^2\\
=&\sum_{w_i,w_j}\left[\langle \boldsymbol{v}_i+\boldsymbol{c}, \boldsymbol{\hat{v}}_j+\boldsymbol{c}\rangle+\Big(b_i-\langle \boldsymbol{v}_i, \boldsymbol{c}\rangle - \frac{|\boldsymbol{c}|^2}{2}\Big)\right.\\
&\qquad\qquad\qquad\qquad\left.+\Big(\hat{b}_j-\langle \boldsymbol{\hat{v}}_j, \boldsymbol{c}\rangle - \frac{|\boldsymbol{c}|^2}{2}\Big)-\log X_{ij}\right]^2\end{aligned}\tag{18}\]
这就是说，如果你有了一组解，那么你将所有词向量加上任意一个常数向量后，它还是一组解！这个问题就严重了，我们无法预估得到的是哪组解，一旦加上的是一个非常大的常向量，那么各种度量都没意义了（比如任意两个词的cos值都接近1）。事实上，对glove生成的词向量进行验算就可以发现，glove生成的词向量，停用词的模长远大于一般词的模长，也就是说一堆词放在一起时，停用词的作用还明显些，这显然是不利用后续模型的优化的。（虽然从目前的关于glove的实验结果来看，是我强迫症了一些。）

互信息估算

点击阅读全文...

在本文中，我们再次对Capsule进行一次分析。

整体上来看，Capsule算法的细节不是很复杂，对照着它的流程把Capsule用框架实现它基本是没问题的。所以，困难的问题是理解Capsule究竟做了什么，以及为什么要这样做，尤其是Dynamic Routing那几步。

为什么我要反复对Capsule进行分析？这并非单纯的“炒冷饭”，而是为了得到对Capsule原理的理解。众所周知，Capsule给人的感觉就是“有太多人为约定的内容”，没有一种“虽然我不懂，但我相信应该就是这样”的直观感受。我希望尽可能将Capsule的来龙去脉思考清楚，使我们能觉得Capsule是一个自然、流畅的模型，甚至对它举一反三。

在《揭开迷雾，来一顿美味的Capsule盛宴》中，笔者先分析了动态路由的结果，然后指出输出是输入的某种聚类，这个“从结果到原因”的过程多多少少有些望文生义的猜测成分；这次则反过来，直接确认输出是输入的聚类，然后反推动态路由应该是怎样的，其中含糊的成分大大减少。两篇文章之间有一定的互补作用。

点击阅读全文...

事实上，在论文《Dynamic Routing Between Capsules》发布不久后，一篇新的Capsule论文《Matrix Capsules with EM Routing》就已经匿名公开了（在ICLR 2018的匿名评审中），而如今作者已经公开，他们是Geoffrey Hinton, Sara Sabour, Nicholas Frosst。不出大家意料，作者果然有Hinton。

大家都知道，像Hinton这些“鼻祖级”的人物，发表出来的结果一般都是比较“重磅”的。那么，这篇新论文有什么特色呢？

在笔者的思考过程中，文章《Understanding Matrix capsules with EM Routing 》给了我颇多启示，知乎上各位大神的相关讨论也加速了我的阅读，在此表示感谢。

论文摘要

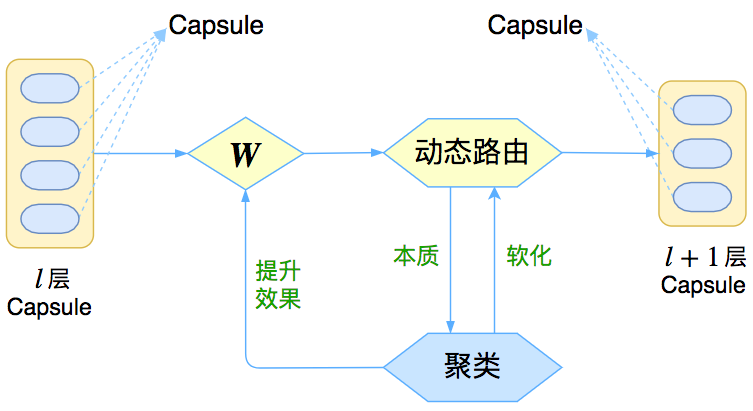
让我们先来回忆一下上一篇介绍《再来一顿贺岁宴：从K-Means到Capsule》中的那个图

Capsule框架的简明示意图

这个图表明，Capsule事实上描述了一个建模的框架，这个框架中的东西很多都是可以自定义的，最明显的是聚类算法，可以说“有多少种聚类算法就有多少种动态路由”。那么这次Hinton修改了什么呢？总的来说，这篇新论文有以下几点新东西：

1、原来用向量来表示一个Capsule，现在用矩阵来表示；

2、聚类算法换成了GMM（高斯混合模型）；

3、在实验部分，实现了Capsule版的卷积。

点击阅读全文...