科学空间是2009年3月建立的，虽然其中经历了一些变动，但是从2009年下半年开始，科学空间就一直在“宇宙驿站”的怀抱之中健康成长着。今天，科学空间即将三岁了（03.16视为科学空间建立的日子），而宇宙驿站则已经十岁了。
在宇宙驿站中，崔博等许许多多人做出了不懈努力，为我们这些科学爱好者提供者免费而优越的服务，BoJone对此有无限的感激之情。与宇宙驿站有种相见恨晚的感觉，不过虽然没有经历建立之初那激动人心的时刻，但是，既然已经和驿站一起、和各位读者一起走了这么久了，就应该一直走下去。
谨此留念
By 崔辰州博士：
十年前的今天，2002年3月12日，在国家天文台LAMOST三楼的小机房里一台从中关村电子市场淘来的电脑对外开始了她的职业生涯，这就是最初的宇宙驿站。
生日祝福
2012年3月28日，我19岁了。
三月是一个很美的月份，我的很多值得纪念的日子都在三月发生，还有好友们都在三月接二连三地生日，几乎让我措手不及了，呵呵。我的同桌黄金，好友家益，还有我自己都在这个月成为十九岁的孩子了。算起来，我应该是“最年轻”的了^_^
3-25-聚餐合照
我的生日收到了许多人的祝福，这让我觉得很意外，我一直觉得，我不善于人际交往，所以不应该会有太多人关注我，但惊喜在我身上发生了。谢谢大家。
人生如梦，繁星流动，和你同路，从不相识开始心接近，默默以真挚待人......这是《朋友》的歌词，也是我们之间的真实写照。感谢上天，让我的人生之路上有你们的相伴，人生因为你们而更加精彩。愿能够与你们一起度过、奋斗过更多的日子！我们相约，我们是一辈子的朋友！
30
Apr
引力透镜——用经典力学推导光的偏转公式
By 苏剑林 | 2012-04-30 | 66604位读者 | 引用引力透镜
————用经典力学推导光的引力偏转角公式
引力透镜效应造成的爱因斯坦十字
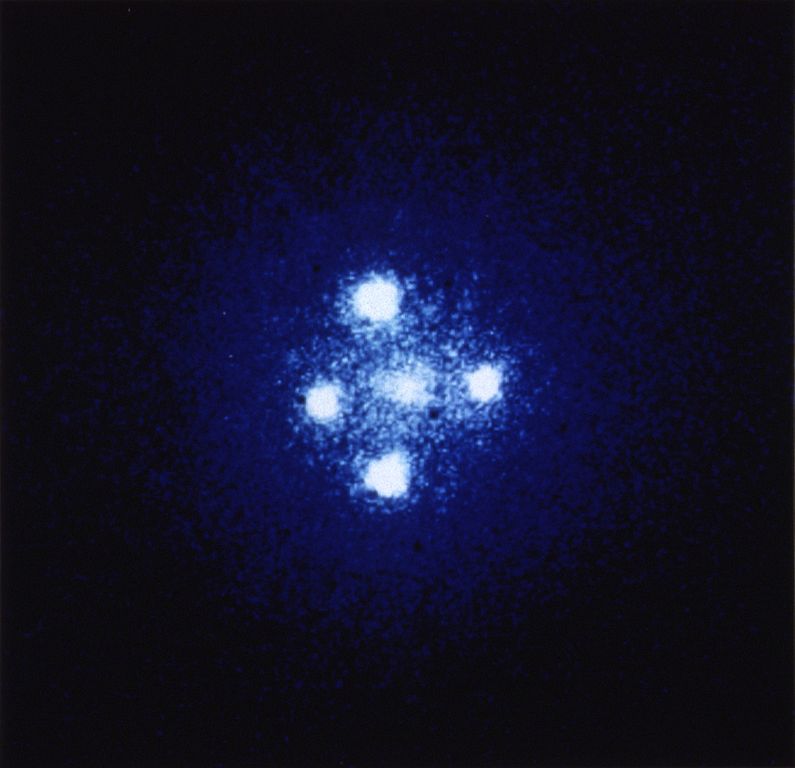
在2012年第四期的《天文爱好者》上，Richard de Grijs（何锐思）教授的《引力透镜——再领科学潮》一文详细而精彩地讲述了有关引力透镜方面的知识，尤其是它在天文方面的重要应用，让我收获颇丰。笔者在赞叹作者优美的文笔和译者程思浩同好的生动翻译之余，也感到了一丝不足。文章主要讲了引力透镜在天文研究中所扮演的重要角色，却未对引力透镜的原理、本质方面多加描述。时空的扭曲是广义相对论给出的答案，可是难道仅仅从经典力学就不能领略丝毫？藉此，BoJone这在里对引力透镜多说些东西，与大家相互学习研究。当然，由于我只是一个初出茅庐的业余爱好者，其中的不当之处还望各位斧正。
1
May
相对论、对称和第四维
By 苏剑林 | 2012-05-01 | 85250位读者 | 引用这篇文章其实在年初就完成了。
众所周知，我们生活在一个平坦的世界中。正如我们能够感受到的那样，在这个被称为“欧几里得平直空间”的世界里，空间里两点间的最短曲线是两点间的直线段，空间里的任意直角三角形都满足勾股定理，每个物体都有着自己的长、宽、高，它们都随着时间的流逝而运动着。这种世界观把时间独立于空间之外，作为一个独特的研究对象。但是自爱因斯坦在1905年发表狭义相对论以来，我们的宇宙就被描述成为了由三维空间和一维时间组成的“四维时空”，在这里，时间和空间的地位是等价的。不少同好们也许会感到非常困惑：即使证明了时间与空间的确存在着某种联系，也不必要把时间描述成是世界的一维吧？在我们的感官里，时间明明就和空间的三维差别甚大，时间和空间怎么能够等同起来呢？其实答案很简单：为了美。把时间看成与空间等价的一维之后，整个力学体系体现出一种前所未有的对称美，这种美不仅让人赏心悦目，而且极大地方便了我们进一步处理问题。
对称
14
Jan
诡异的Dirac函数
By 苏剑林 | 2013-01-14 | 48301位读者 | 引用量子力学中有一个很诡异的函数——Dirac函数，它似乎在物理的不少领域都有很大作用，它也具有明显的物理意义，但认真地看它却又感觉它根本就不是函数！这个“似而非是”的东西究竟是什么呢？让我们从一个物理问题引入：
设想一条质量为1，长度为$2l$的均匀直线，很显然直线的密度为$\rho=\frac{1}{2l}$；将直线的中点放置于坐标轴的原点，我们就有
$$\rho(x)=\left\{ \begin{array}{c}\frac{1}{2l} (-l \leq x \leq l)\\0 (x < -l , x > l)\end{array}\right.$$
所以有
$$\int_{-\infty}^{+\infty} \rho(x)dx=1$$
23
May
高考倒计时15天...
By 苏剑林 | 2012-05-23 | 42629位读者 | 引用
12
Jun
费曼积分法——积分符号内取微分(2)
By 苏剑林 | 2012-06-12 | 100437位读者 | 引用上一篇文章我对“费曼积分法”做了一个简单的介绍，并通过举例来初步展示了它的操作步骤。但是，要了解一个方法，除了知道它能够干什么之外，还必须了解它的原理和方法，这样我们才能够更好地掌握它。因此，我们需要建立“积分符号内取微分”的一般理论，为进一步的应用奠基。
一般原理
我们记
$$G(a)=\int_{m(a)}^{n(a)} f(x,a)dx$$
在这里，f(x,a)是带有参数a的关于x的函数，而积分区间是关于参数a的两个函数，这样的积分也叫变限积分，可以理解为是普通定积分的推广。我们记F(x,a)为f(x,a)的原函数，也就是说$\frac{\partial F(x,a)}{\partial x}=f(x,a)$，那么按照微积分基本定理，我们就有：
$$G(a)=F(n(a),a)-F(m(a),a)$$
刚从天堂（镇）赶回来，这次大概一个星期的骑自行车游新兴之旅基本结束了。
这次行程我们总共穿越了太平、新城、洞口、车岗、六祖、东成、稔村、水台、勒竹、河头、天堂，共十一个镇，没有到过的地方还有共成、船岗、大江、里洞等，这些地方骑单车可能比较困难，有时间坐车去逛逛。
这次旅行可谓大有收获！各地的“到此一游”让我们增长了不少见识，加深了对我们家乡的了解；一路上大家嘻嘻哈哈，乐趣无穷，为我们的友谊增添了美好的点缀；到同学家玩玩闹闹，也加强了我们之间的联系，同样乐趣无穷；还有增加了探路找路的技术......
感谢所有陪我们一起玩、一起疯的同学，感谢所有给我们帮助的同学，人生因为你们的存在而更加精彩！
最近评论