让炼丹更科学一些(一):SGD的平均损失收敛
By 苏剑林 | 2023-12-19 | 35282位读者 | 引用很多时候我们将深度学习模型的训练过程戏称为“炼丹”,因为整个过程跟古代的炼丹术一样,看上去有一定的科学依据,但整体却给人一种“玄之又玄”的感觉。尽管本站之前也关注过一些优化器相关的工作,甚至也写过《从动力学角度看优化算法》系列,但都是比较表面的介绍,并没有涉及到更深入的理论。为了让以后的炼丹更科学一些,笔者决定去补习一些优化相关的理论结果,争取让炼丹之路多点理论支撑。
在本文中,我们将学习随机梯度下降(SGD)的一个非常基础的收敛结论。虽然现在看来,该结论显得很粗糙且不实用,但它是优化器收敛性证明的一次非常重要的尝试,特别是它考虑了我们实际使用的是随机梯度下降(SGD)而不是全量梯度下降(GD)这一特性,使得结论更加具有参考意义。
问题设置
设损失函数是$L(\boldsymbol{x},\boldsymbol{\theta})$,其实$\boldsymbol{x}$是训练集,而$\boldsymbol{\theta}\in\mathbb{R}^d$是训练参数。受限于算力,我们通常只能执行随机梯度下降(SGD),即每步只能采样一个训练子集来计算损失函数并更新参数,假设采样是独立同分布的,第$t$步采样到的子集为$\boldsymbol{x}_t$,那么我们可以合理地认为实际优化的最终目标是
\begin{equation}L(\boldsymbol{\theta}) = \lim_{T\to\infty}\frac{1}{T}\sum_{t=1}^T L(\boldsymbol{x}_t,\boldsymbol{\theta})\label{eq:loss}\end{equation}
重温SSM(一):线性系统和HiPPO矩阵
By 苏剑林 | 2024-05-24 | 38294位读者 | 引用前几天,笔者看了几篇介绍SSM(State Space Model)的文章,才发现原来自己从未认真了解过SSM,于是打算认真去学习一下SSM的相关内容,顺便开了这个新坑,记录一下学习所得。
SSM的概念由来已久,但这里我们特指深度学习中的SSM,一般认为其开篇之作是2021年的S4,不算太老,而SSM最新最火的变体大概是去年的Mamba。当然,当我们谈到SSM时,也可能泛指一切线性RNN模型,这样RWKV、RetNet还有此前我们在《Google新作试图“复活”RNN:RNN能否再次辉煌?》介绍过的LRU都可以归入此类。不少SSM变体致力于成为Transformer的竞争者,尽管笔者并不认为有完全替代的可能性,但SSM本身优雅的数学性质也值得学习一番。
尽管我们说SSM起源于S4,但在S4之前,SSM有一篇非常强大的奠基之作《HiPPO: Recurrent Memory with Optimal Polynomial Projections》(简称HiPPO),所以本文从HiPPO开始说起。
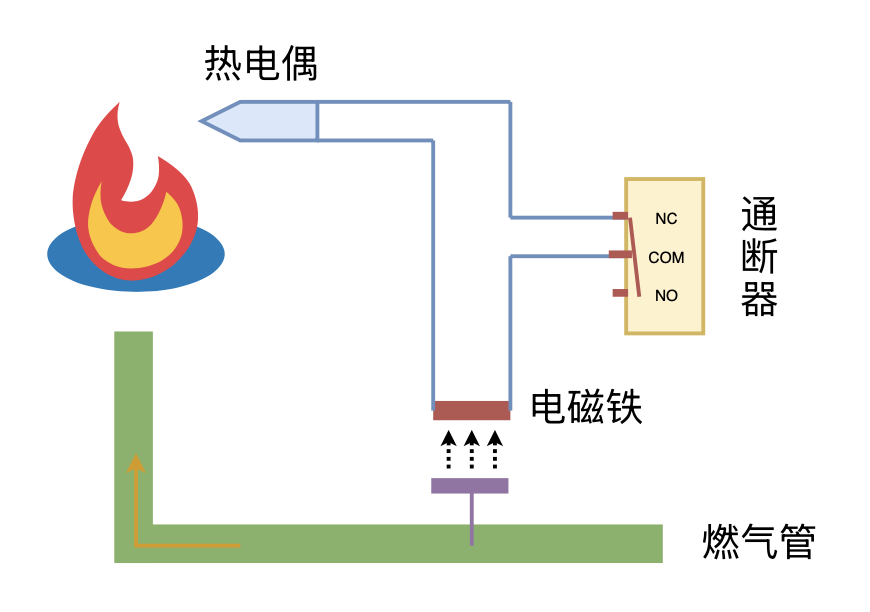
利用“熄火保护 + 通断器”实现燃气灶智能关火
By 苏剑林 | 2024-09-26 | 12050位读者 | 引用VQ的又一技巧:给编码表加一个线性变换
By 苏剑林 | 2024-11-06 | 4347位读者 | 引用在《VQ的旋转技巧:梯度直通估计的一般推广》中,我们介绍了VQ(Vector Quantization)的Rotation Trick,它的思想是通过推广VQ的STE(Straight-Through Estimator)来为VQ设计更好的梯度,从而缓解VQ的编码表坍缩、编码表利用率低等问题。
无独有偶,昨天发布在arXiv上的论文《Addressing Representation Collapse in Vector Quantized Models with One Linear Layer》提出了改善VQ的另一个技巧:给编码表加一个线性变换。这个技巧单纯改变了编码表的参数化方式,不改变VQ背后的理论框架,但实测效果非常优异,称得上是简单有效的经典案例。
一道从小学到高中都可能考到的题目
By 苏剑林 | 2009-09-20 | 35106位读者 | 引用背景资料:从数字看诺贝尔物理学奖
By 苏剑林 | 2009-10-07 | 15022位读者 | 引用2009年诺贝尔物理学奖于6日公布,英国华裔科学家高锟以及美国科学家威拉德·博伊尔和乔治·史密斯摘得桂冠。以下是关于诺贝尔物理学奖的一些数字:
1、诺贝尔物理学奖从1901年开始颁奖,但并非年年颁奖,1916年、1931年、1934年、1940年、1941年和1942年都没有颁奖。之所以这6年没颁奖,是因为第一次世界大战和第二次世界大战的发生,或因为没有人符合获得诺贝尔奖的那些条件。
2、到今年为止,一名科学家独享诺贝尔物理学奖有47次,而两名科学家和三名科学家分享诺贝尔物理学奖的次数相同,都是28次。按诺贝尔基金会的规定,不会有3人以上同时获得一个奖项。
从牛顿力学角度研究宇宙学
By 苏剑林 | 2010-06-17 | 47117位读者 | 引用不少天文爱好者对宇宙学这方面的内容“听而生畏”,觉得没有爱因斯坦的广义相对论等复杂理论基础是不可理解的。的确,这种观点没有错,当前的宇宙学对宇宙的精确描述,的确是建立在广义相对论和量子力学等理论的基础之上的。BoJone也只是在书上略略浏览,根本谈不上有什么了解。但是,对于一般的天文爱好者来说,只要对牛顿力学和微积分有一定的了解,就可以对我们的宇宙有一个大概的描述,也能够得出很多令人惊喜的结论。相信进行了这项工作之后,很多爱好者都会改观:原来宇宙学也并不是那么难...并且能够得出这样的一个结论:广义相对论虽然对牛顿引力理论进行了彻底的改革,但是从数学的角度来讲,它仅仅对牛顿力学进行了修正。
当概率遇上复变:从二项分布到泊松分布
By 苏剑林 | 2015-01-13 | 24487位读者 | 引用泊松分布,适合于描述单位时间内随机事件发生的次数的概率分布,如某一服务设施在一定时间内受到的服务请求的次数、汽车站台的候客人数等。[维基百科]泊松分布也可以作为小概率的二项分布的近似,其推导过程在一般的概率论教材都会讲到。可是一般教材上给出的证明并不是那么让人赏心悦目,如《概率论与数理统计教程》(第二版,茆诗松等编)的第98页就给出的证明过程。那么,哪个证明过程才更让人点赞呢?我认为是利用母函数的证明。
二项分布的母函数为
$$\begin{equation}(q+px)^n,\quad q=1-p\end{equation}$$








最近评论