科学空间|Scientific Spaces

在上一篇文章中，我们已经得到了电偶极子的等势面和电场线方程，这应该可以让我们对电偶极子的力场情况有个大致的了解了。当然，我们还是希望能够求出在这样的一个受力情况下，一个带电粒子是如何运动的。简单起见，在下面的探讨中，我们假定带电粒子的质量和电荷量均为1，至于电荷的正负，可以通过改变在$U=-\frac{k \cos\theta}{r^2}$中的k值的正负来控制。我们使用的工具依旧是理论力学中的欧拉-拉格朗日方程。

也许不少读者始终对公式感到头疼，更不用说是博大精深的理论力学了。但是请相信我，如果你花一点点心思去弄懂用变分法研究力学（或其他物理系统，但我目前只会用于力学）的基本思路和步骤，那么对你的物理研究是大有裨益的。因为在我眼中，学习了一丁点的理论力学知识后，我看到的只有物理的简洁与和谐。有兴趣的朋友可以看看我的那几篇《自然极值》等相关文章。

首先写出动能的表达式：$T=\frac{1}{2} (\dot{r}^2+r^2 \dot{\theta}^2)$

还有势能：$U=-\frac{k \cos\theta}{r^2}$

点击阅读全文...

上一篇文章讲的是基于词典和AC自动机的快速分词。基于词典的分词有一个明显的优点，就是便于维护，容易适应领域。如果迁移到新的领域，那么只需要添加对应的领域新词，就可以实现较好地分词。当然，好的、适应领域的词典是否容易获得，这还得具体情况具体分析。本文要讨论的就是新词发现这一部分的内容。

这部分内容在去年的文章《新词发现的信息熵方法与实现》已经讨论过了，算法是来源于matrix67的文章《互联网时代的社会语言学：基于SNS的文本数据挖掘》。在那篇文章中，主要利用了三个指标——频数、凝固度（取对数之后就是我们所说的互信息熵）、自由度（边界熵）——来判断一个片段是否成词。如果真的动手去实现过这个算法的话，那么会发现有一系列的难度。首先，为了得到$n$字词，就需要找出$1\sim n$字的切片，然后分别做计算，这对于$n$比较大时，是件痛苦的时间；其次，最最痛苦的事情是边界熵的计算，边界熵要对每一个片段就行分组统计，然后再计算，这个工作量的很大的。本文提供了一种方案，可以使得新词发现的计算量大大降低。

点击阅读全文...

迄今为止，前四篇文章已经介绍了分词的若干思路，其中有基于最大概率的查词典方法、基于HMM或LSTM的字标注方法等。这些都是已有的研究方法了，笔者所做的就只是总结工作而已。查词典方法和字标注各有各的好处，我一直在想，能不能给出一种只需要大规模语料来训练的无监督分词模型呢？也就是说，怎么切分，应该是由语料来决定的，跟语言本身没关系。说白了，只要足够多语料，就可以告诉我们怎么分词。

看上去很完美，可是怎么做到呢？《2.基于切分的新词发现》中提供了一种思路，但是不够彻底。那里居于切分的新词发现方法确实可以看成一种无监督分词思路，它就是用一个简单的凝固度来判断某处该不该切分。但从分词的角度来看，这样的分词系统未免太过粗糙了。因此，我一直想着怎么提高这个精度，前期得到了一些有意义的结果，但都没有得到一个完整的理论。而最近正好把这个思路补全了。因为没有查找到类似的工作，所以这算是笔者在分词方面的一点原创工作了。

语言模型

首先简单谈一下语言模型。

点击阅读全文...

这个系列慢慢写到第7篇，基本上也把分词的各种模型理清楚了，除了一些细微的调整（比如最后的分类器换成CRF）外，剩下的就看怎么玩了。基本上来说，要速度，就用基于词典的分词，要较好地解决组合歧义何和新词识别，则用复杂模型，比如之前介绍的LSTM、FCN都可以。但问题是，用深度学习训练分词器，需要标注语料，这费时费力，仅有的公开的几个标注语料，又不可能赶得上时效，比如，几乎没有哪几个公开的分词系统能够正确切分出“扫描二维码，关注微信号”来。

本文就是做了这样的一个实验，仅用一个词典，就完成了一个深度学习分词器的训练，居然效果还不错！这种方案可以称得上是半监督的，甚至是无监督的。

点击阅读全文...

如果依次阅读该系列文章的读者，就会发现这个系列共提供了两种从0到1的无监督分词方案，第一种就是《【中文分词系列】 2. 基于切分的新词发现》，利用相邻字凝固度（互信息）来做构建词库（有了词库，就可以用词典法分词）；另外一种是《【中文分词系列】 5. 基于语言模型的无监督分词》，后者基本上可以说是提供了一种完整的独立于其它文献的无监督分词方法。

但总的来看，总感觉前面一种很快很爽，却又显得粗糙；后面一种很好很强大，却又显得太过复杂（viterbi是瓶颈之一）。有没有可能在两者之间折中一下？这就导致了本文的结果，达到了速度与效果的平衡。至于为什么说“更好”？因为笔者研究词库构建也有一段时间了，以往构建的词库总不能让人（让自己）满意，生成的词库一眼看上去，都能够扫到不少不合理的地方，真的要用得需要经过较多的人工筛选。而这一次，一次性生成的词库，一眼扫过去，不合理的地方少了很多，如果不细看，可能就发现不了了。

分词的目的

点击阅读全文...

大概在1年前，我们提出了旋转位置编码（RoPE），并发布了对应的预训练模型RoFormer。随着时间的推移，RoFormer非常幸运地得到了越来越多的关注和认可，比如EleutherAI新发布的60亿和200亿参数的GPT模型中就用上了RoPE位置编码，Google新提出的FLASH模型论文中则明确指出了RoPE对Transformer效果有明显的提升作用。

与此同时，我们也一直在尝试继续加强RoFormer模型，试图让RoFormer的性能“更上一层楼”。经过近半年的努力，我们自认为取得了还不错的成果，因此将其作为“RoFormerV2”正式发布：

Github：https://github.com/ZhuiyiTechnology/roformer-v2

点击阅读全文...

上集回顾

在上一篇文章中，笔者分享了自己对最大熵原理的认识，包括最大熵原理的意义、最大熵原理的求解以及一些简单而常见的最大熵原理的应用。在上一篇的文末，我们还通过最大熵原理得到了正态分布，以此来说明最大熵原理的深刻内涵和广泛意义。

本文中，笔者将介绍基于最大熵原理的模型——最大熵模型。本文以有监督的分类问题来介绍最大熵模型，所谓有监督，就是基于已经标签好的数据进行的。

事实上，第二篇文章的最大熵原理才是主要的，最大熵模型，实质上只是最大熵原理的一个延伸，或者说应用。

最大熵模型

分类：意味着什么？

在引入最大熵模型之前，我们先来多扯一点东西，谈谈分类问题意味着什么。假设我们有一批标签好的数据：
$$\begin{array}{c|cccccccc}
\hline
\text{数据}x & 1 & 2 & 3 & 4 & 5 & 6 & \dots & 100 \\
\hline
\text{标签}y & 1 & 0 & 1 & 0 & 1 & 0 & \dots & 0\\
\hline \end{array}$$

点击阅读全文...

过去虽然没有细看，但印象里一直觉得变分自编码器（Variational Auto-Encoder，VAE）是个好东西。于是趁着最近看概率图模型的三分钟热度，我决定也争取把VAE搞懂。于是乎照样翻了网上很多资料，无一例外发现都很含糊，主要的感觉是公式写了一大通，还是迷迷糊糊的，最后好不容易觉得看懂了，再去看看实现的代码，又感觉实现代码跟理论完全不是一回事啊。

终于，东拼西凑再加上我这段时间对概率模型的一些积累，并反复对比原论文《Auto-Encoding Variational Bayes》，最后我觉得我应该是想明白了。其实真正的VAE，跟很多教程说的的还真不大一样，很多教程写了一大通，都没有把模型的要点写出来～于是写了这篇东西，希望通过下面的文字，能把VAE初步讲清楚。

分布变换

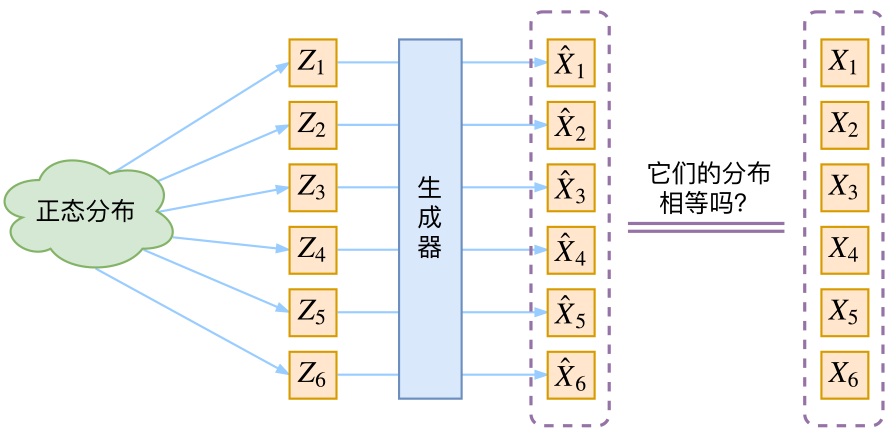
通常我们会拿VAE跟GAN比较，的确，它们两个的目标基本是一致的——希望构建一个从隐变量$Z$生成目标数据$X$的模型，但是实现上有所不同。更准确地讲，它们是假设了$Z$服从某些常见的分布（比如正态分布或均匀分布），然后希望训练一个模型$X=g(Z)$，这个模型能够将原来的概率分布映射到训练集的概率分布，也就是说，它们的目的都是进行分布之间的变换。

生成模型的难题就是判断生成分布与真实分布的相似度，因为我们只知道两者的采样结果，不知道它们的分布表达式

点击阅读全文...