科学空间|Scientific Spaces

圆上的有理点

我们在这个系列的文章之中，探索了一些有关环和域的基本知识，并用整环以及唯一分解性定理证明了费马大定理在n=3和n=4时的情形。使用高斯整数环或者艾森斯坦整数环的相关知识，相对而言是属于近代的比较“高端”的代数内容（高斯生于1777年，艾森斯坦生于1823年，然而艾森斯坦英年早逝，只活到了1852年，高斯还活到了1855年。）。如果“顺利”的话，我们可以用这些“高端”的工具证明解的不存在性，或者求出通解（如果有解的话）。

然而，对于初等数论来讲，复数环和域的知识的门槛还是有点高了。其次，环和域是一个比较“强”的工具。这里的“强”有点“强势”的意味，是指这样的意思：如果它成功的话，它能够“一举破城”，把通解都求出来（或者证明解的不存在）；如果它不成功的话，那么往往就连一点非平凡的解都求不出来。可是，有些问题是求出一部分解都已经很困难了，更不用说求出通解了（我们以后在研究$x^4+y^4 = z^4 + w^4 $的整数解的时候，就能深刻体会这点。）。因此，对于这些问题，单纯用环域的思想，很难给予我们（至少一部分）解。（当然，问题是如何才算是“单纯”，这也很难界定。这里的评论是比较粗糙的。）

点击阅读全文...

本文我们继续之前的变分自编码器系列，分析一下如何防止NLP中的VAE模型出现“KL散度消失（KL Vanishing）”现象。本文受到参考文献是ACL 2020的论文《A Batch Normalized Inference Network Keeps the KL Vanishing Away》的启发，并自行做了进一步的完善。

值得一提的是，本文最后得到的方案还是颇为简洁的——只需往编码输出加入BN（Batch Normalization），然后加个简单的scale——但确实很有效，因此值得正在研究相关问题的读者一试。同时，相关结论也适用于一般的VAE模型（包括CV的），如果按照笔者的看法，它甚至可以作为VAE模型的“标配”。

最后，要提醒读者这算是一篇VAE的进阶论文，所以请读者对VAE有一定了解后再来阅读本文。

VAE简单回顾

这里我们简单回顾一下VAE模型，并且讨论一下VAE在NLP中所遇到的困难。关于VAE的更详细介绍，请读者参考笔者的旧作《变分自编码器（一）：原来是这么一回事》、《变分自编码器（二）：从贝叶斯观点出发》等。

VAE的训练流程

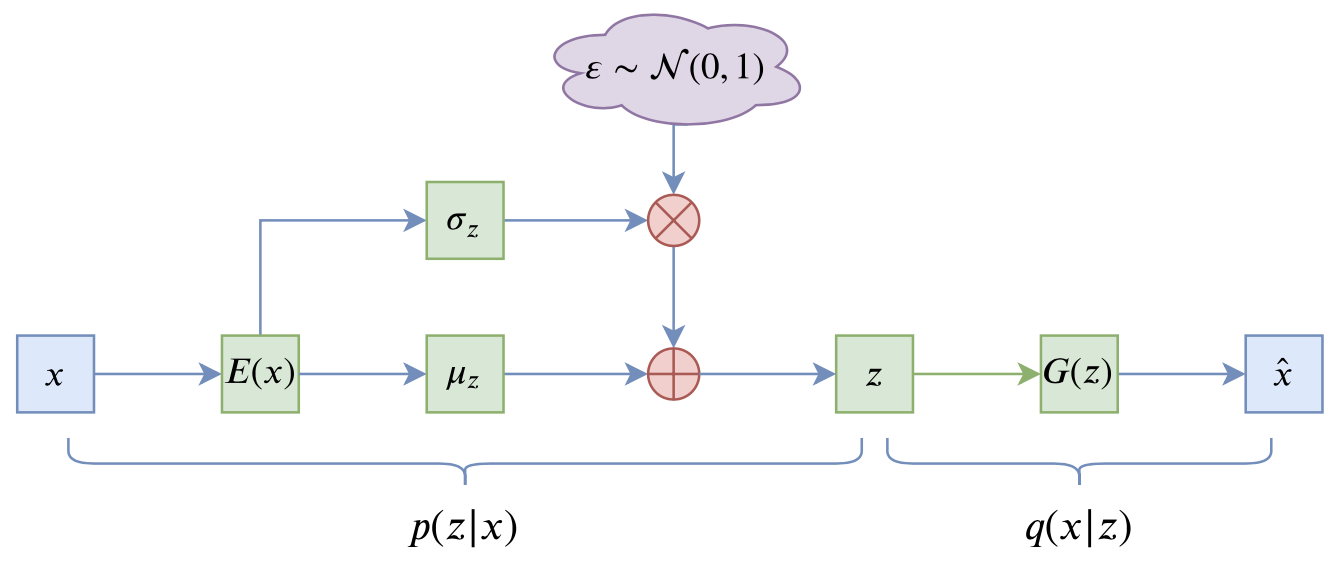
VAE的训练流程大概可以图示为

VAE训练流程图示

点击阅读全文...

首先谈点题外话，关于本系列以及本博客的写作。其实本博客的写作内容，代表了笔者在这段时间附近的研究成果。也就是说，我此时在写这篇文章，其实表明我这段时间正在研究这个问题。而接下来的研究是否有结果，有怎样的结果，则是完全不知道的。所以，我在写这篇文章的时候，并不确定下一篇文章会写些什么。有些类似的话题，我会放在同一个系列去写。但不管怎样，这些文章可能并不遵循常规的教学或者学习思路，有些内容还可能与主流的思想方法有相当出入，请读者见谅，望大家继续支持！

上一篇我们谈到了切线法来求二次和三次曲线的有理点。切线法在寻找不高于三次的曲线上的有理点是很成功的，可是对于更高次的曲线有没有类似的方法呢？换句话说，有没有推广的可能性。我们从纯代数的角度来回复一下切线法生效的原因。切线法，更一般的是割线法，能够起作用，主要是因为如果有理系数的三次方程有两个有理数的根，那么第三个根肯定是有理数。如果只有一个已知的有理根，那么就可以让两个根重合为已知的那个根，从而割线变成了切线。

点击阅读全文...

从小学到大学都可能被问到的但却又不容易很好地回答的问题中，“0.999...究竟等不等于1”肯定也算是相当经典的一个。然而，要清楚地回答这个问题并不容易，很多时候被提问者都会不自觉地弄晕，甚至有些“民科”还以这个问题“创造了新数学”。

本文试图就这个问题，给出比较通俗但比较严谨的回答。

什么是相等？

要回答0.999...等不等于1，首先得定义“相等”！什么才算相等？难道真的要写出来一模一样才叫相等吗？如果是这样的话，那么2-1都不等于1了，因为2-1跟1看起来都不一样啊。

显然我们需要给“相等”做出比较严格但是又让人公认的定义，才能对相等进行判断，显然，下面的定义是能够让很多人接受的：

$a = b$等切仅当$|a-b|=0$。

点击阅读全文...

前言

今天在QQ群里的讨论中看到了focal loss，经搜索它是Kaiming大神团队在他们的论文《Focal Loss for Dense Object Detection》提出来的损失函数，利用它改善了图像物体检测的效果。不过我很少做图像任务，不怎么关心图像方面的应用。本质上讲，focal loss就是一个解决分类问题中类别不平衡、分类难度差异的一个loss，总之这个工作一片好评就是了。大家还可以看知乎的讨论：
《如何评价kaiming的Focal Loss for Dense Object Detection？》

看到这个loss，开始感觉很神奇，感觉大有用途。因为在NLP中，也存在大量的类别不平衡的任务。最经典的就是序列标注任务中类别是严重不平衡的，比如在命名实体识别中，显然一句话里边实体是比非实体要少得多，这就是一个类别严重不平衡的情况。我尝试把它用在我的基于序列标注的问答模型中，也有微小提升。嗯，这的确是一个好loss。

接着我再仔细对比了一下，我发现这个loss跟我昨晚构思的一个loss具有异曲同工之理！这就促使我写这篇博文了。我将从我自己的思考角度出发，来分析这个问题，最后得到focal loss，也给出我昨晚得到的类似的loss。

点击阅读全文...

写在前面：前面的博文已经提过，在上个月我参加了第四届泰迪杯数据挖掘竞赛，做的是A题，跟OCR系统有些联系，还承诺过会把最终的结果开源。最近忙于毕业、搬东西，一直没空整理这些内容，现在抽空整理一下。

把结果发出来，并不是因为结果有多厉害、多先进（相反，当我对比了百度的这篇论文《基于深度学习的图像识别进展：百度的若干实践》之后，才发现论文的内容本质上还是传统那一套，远远还跟不上时代的潮流），而是因为虽然OCR技术可以说比较成熟了，但网络上根本就没有对OCR系统进行较为详细讲解的文章，而本文就权当补充这部分内容吧。我一直认为，技术应该要开源才能得到发展（当然，在中国这一点也确实值得商榷，因为开源很容易造成山寨），不管是数学物理研究还是数据挖掘，我大多数都会发表到博客中，与大家交流。

点击阅读全文...

数据验证

尽管在测试环境下模型工作良好，但是实践是检验真理的唯一标准. 在本节中，我们通过自己的模型，与京东的测试数据进行比较验证.

衡量OCR系统的好坏有两部分内容：(1)是否成功地圈出了文字；(2)对于圈出来的文字，有没有成功识别. 我们采用评分的方法，对每一张图片的识别效果进行评分. 评分规则如下：

如果圈出的文字区域能够跟京东提供的检测样本的box文件中匹配，那么加1分，如果正确识别出文字来，另外加1分，最后每张图片的分数是前面总分除以文字总数.

按照这个规则，每张图片的评分最多是2分，最少是0分. 如果评分超过1，说明识别效果比较好了. 经过京东的测试数据比较，我们的模型平均评分大约是0.84，效果差强人意。

点击阅读全文...

开始研究僧之旅，希望有一天能企及扫地僧的境界。

进入中山大学后，各种郁闷的事情就来了。首先最郁闷的就是开学时间特早，8月26日开学，感觉至少比一般学校早了一星期，开学这么早有意思么～～接着就是感觉中大的管理制度各种混乱，比我本科的华师差多了。好吧，这些琐事先不吐槽，接下来弄校园网，这是作死的开始。

我们是在南校区的，校园网是通过锐捷客户端来认证的，而我是用macbook的，不过中大这边还很人性化地提供了Mac版的锐捷，体积就1M左右，挺好的。但众所周知，macbook并没有有线网卡，每次我上网都得插着个USB网卡然后连着网线，这该有多郁闷。于是想办法通过路由器拨号。我也不算没经验的了，对openwrt这个系统有过一定研究，以前在本科的时候也是锐捷，可以用mentohust替代拨号，很简单。于是我在这里重复这样的过程，发现一直认证失败，按照网上提示的各种方法，都无法解决。

经过研究，我发现在Windows下，这里就只能用官方提供了锐捷4.90版本，从其他地方下载的更高级或者更低级的锐捷，都无法通过验证。估计就是因为这个机制，导致了mentohust难以通过验证。而且网上流行的mentohust都是基于V2协议的，但4.90是基于V4的。后来我又去下载了V4版本的进行交叉编译，测试发现还不成功。几近绝望的时候，我发现了mentohust-proxy，一个mentohust的改进版，让我找到了希望。（怎么找到它？我是直接到github搜索了，因为实在没辙了～～）

原理很简单，如果直接通过mentohust无法完成认证，那么就通过代理模式，由电脑来完成认证，而mentohust只需要负责发送心跳包维持联网就行。这是个很折中的方案，但应该说是一个很通用的方案，因为它的成功与否，基本就取决于自己电脑的锐捷客户端而已。看到这个方案，我就知道有戏了，于是赶紧补习了一下交叉编译的知识，最后成功编译好了，并且在路由上成功地完成了认证。

点击阅读全文...