从一个单位向量变换到另一个单位向量的正交矩阵
By 苏剑林 | 2021-06-05 | 64234位读者 |这篇文章我们来讨论一个比较实用的线性代数问题:
给定两个$d$维单位(列)向量$\boldsymbol{a},\boldsymbol{b}$,求一个正交矩阵$\boldsymbol{T}$,使得$\boldsymbol{b}=\boldsymbol{T}\boldsymbol{a}$。
由于两个向量模长相同,所以很显然这样的正交矩阵必然存在,那么,我们怎么把它找出来呢?
二维 #
不难想象,这本质上就是$\boldsymbol{a},\boldsymbol{b}$构成的二维子平面下的向量变换(比如旋转或者镜面反射)问题,所以我们先考虑$d=2$的情形。
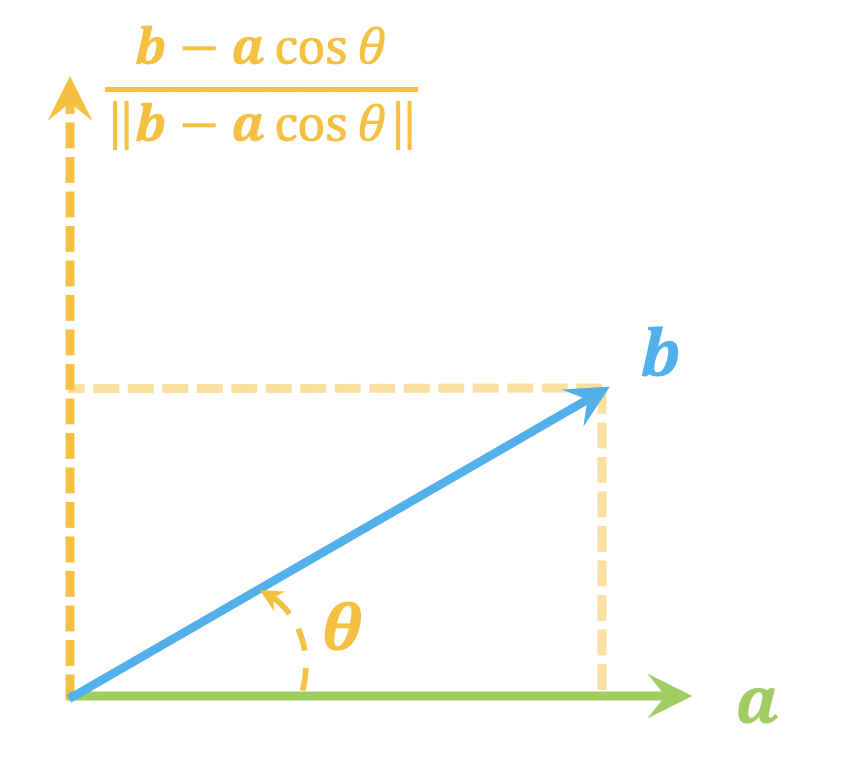
如上图所示,通过正交分解我们可以得到跟$\boldsymbol{a}$垂直的向量$\boldsymbol{b} - \boldsymbol{a}\cos\theta$,然后标准化后就可以得到一个标准正交基:
\begin{equation}\boldsymbol{Q} = \begin{pmatrix}\boldsymbol{a} & \frac{\boldsymbol{b} - \boldsymbol{a}\cos\theta}{\Vert \boldsymbol{b} - \boldsymbol{a}\cos\theta\Vert}\end{pmatrix}\end{equation}
其中$\theta$是$\boldsymbol{a},\boldsymbol{b}$的夹角。在此坐标基下,$\boldsymbol{a}$的坐标为$(1,0)$,$\boldsymbol{b}$的坐标为$(\cos\theta,\sin\theta)$,即
\begin{equation}\boldsymbol{a}=\boldsymbol{Q}\begin{pmatrix}1 \\ 0\end{pmatrix},\quad \boldsymbol{b}=\boldsymbol{Q}\begin{pmatrix}\cos\theta \\ \sin\theta\end{pmatrix}\end{equation}
因此
\begin{equation}\boldsymbol{b}=\boldsymbol{Q}\boldsymbol{R}\begin{pmatrix}1 \\ 0\end{pmatrix}=\boldsymbol{Q}\boldsymbol{R}\boldsymbol{Q}^{\top}\boldsymbol{a}\label{eq:ba}\end{equation}
这里$\boldsymbol{R}$有两个选择:
\begin{equation}\boldsymbol{R}=\begin{pmatrix}\cos\theta & -\sin\theta \\ \sin\theta & \cos\theta\end{pmatrix}\quad \text{或} \quad\boldsymbol{R}=\begin{pmatrix}\cos\theta & \sin\theta \\ \sin\theta & -\cos\theta\end{pmatrix}\end{equation}
从几何意义上来看,前者对应着向量的旋转,后者对应着向量的镜面反射,两者会导致略有不同的最终结果,当然从纯数学来看,它们就是符合要求的正交矩阵而已。式$\eqref{eq:ba}$意味着所寻求的正交矩阵就是
\begin{equation}\boldsymbol{T}=\boldsymbol{Q}\boldsymbol{R}\boldsymbol{Q}^{\top}\end{equation}
多维 #
对于已经理解了上述过程的同学,其实多维情况的思路已经很明朗了。我们也同样先选择一个标准正交基,然后转化为比较简单的情形来解决。由于$d > 2$,所以$\boldsymbol{a}$和$\frac{\boldsymbol{b} - \boldsymbol{a}\cos\theta}{\Vert \boldsymbol{b} - \boldsymbol{a}\cos\theta\Vert}$不够成为一组正交基了,但是理论上来说,我们可以找到$\boldsymbol{e}_3,\cdots,\boldsymbol{e}_d$,使得
\begin{equation}\tilde{\boldsymbol{Q}} = \begin{pmatrix}\boldsymbol{a} & \frac{\boldsymbol{b} - \boldsymbol{a}\cos\theta}{\Vert \boldsymbol{b} - \boldsymbol{a}\cos\theta\Vert} & \boldsymbol{e}_3 & \cdots & \boldsymbol{e}_d\end{pmatrix} = \begin{pmatrix}\boldsymbol{Q} & \boldsymbol{E}\end{pmatrix}\end{equation}
构成一个标准正交基,其中
\begin{equation}\boldsymbol{Q}=\begin{pmatrix}\boldsymbol{a} & \frac{\boldsymbol{b} - \boldsymbol{a}\cos\theta}{\Vert \boldsymbol{b} - \boldsymbol{a}\cos\theta\Vert} \end{pmatrix}\in\mathbb{R}^{d\times 2},\quad\boldsymbol{E}=\begin{pmatrix}\boldsymbol{e}_3 & \cdots & \boldsymbol{e}_d\end{pmatrix}\in\mathbb{R}^{d\times (d-2)}\end{equation}
此时
\begin{equation}\boldsymbol{a}=\tilde{\boldsymbol{Q}}\begin{pmatrix}1 \\ 0 \\ 0 \\ \vdots \\ 0\end{pmatrix},\quad \boldsymbol{b}=\tilde{\boldsymbol{Q}}\begin{pmatrix}\cos\theta \\ \sin\theta \\ 0 \\ \vdots \\ 0\end{pmatrix}=\tilde{\boldsymbol{Q}}\begin{pmatrix} \boldsymbol{R} & \boldsymbol{0}_{2\times(d-2)} \\ \boldsymbol{0}_{(d-2)\times 2} & \boldsymbol{I}_{(d-2)\times(d-2)}\end{pmatrix}\begin{pmatrix}1 \\ 0 \\ 0 \\ \vdots \\ 0\end{pmatrix}\end{equation}
这里的$\boldsymbol{R}$定义同前。所以最后要寻求的矩阵就是:
\begin{equation}\boldsymbol{T}=\tilde{\boldsymbol{Q}}\begin{pmatrix} \boldsymbol{R} & \boldsymbol{0}_{2\times(d-2)} \\ \boldsymbol{0}_{(d-2)\times 2} & \boldsymbol{I}_{(d-2)\times(d-2)}\end{pmatrix}\tilde{\boldsymbol{Q}}^{\top}\label{eq:final-1}\end{equation}
化简 #
将矩阵$\eqref{eq:final-1}$用分块矩阵$\boldsymbol{Q},\boldsymbol{R},\boldsymbol{E}$表达出来,结果是$\boldsymbol{Q}\boldsymbol{R}\boldsymbol{Q}^{\top}+\boldsymbol{E}\boldsymbol{E}^{\top}$,注意到我们还有$\tilde{\boldsymbol{Q}}\tilde{\boldsymbol{Q}}^{\top}=\boldsymbol{I}_{d\times d}$,这意味着$\boldsymbol{E}\boldsymbol{E}^{\top}=\boldsymbol{I}_{d\times d} - \boldsymbol{Q}\boldsymbol{Q}^{\top}$,所以变换$\eqref{eq:final-1}$最终可以写成:
\begin{equation}\boldsymbol{T}=\boldsymbol{Q}\boldsymbol{R}\boldsymbol{Q}^{\top}+\boldsymbol{I}_{d\times d} - \boldsymbol{Q}\boldsymbol{Q}^{\top}\end{equation}
这个结果比较让人意外的一点是,带有随机性的$\boldsymbol{E}$被消去了,得到的是一个确定性的结果。我们还可以把$\boldsymbol{Q},\boldsymbol{R}$的具体形式代进去,进一步简化结果:
\begin{equation}\boldsymbol{T} = \left\{\begin{aligned}\boldsymbol{I}_{d\times d} + 2\boldsymbol{b}\boldsymbol{a}^{\top}-
\frac{(\boldsymbol{a} + \boldsymbol{b})(\boldsymbol{a} + \boldsymbol{b})^{\top}}{1+\cos\theta},\quad &\text{当}\,\boldsymbol{R}=\begin{pmatrix}\cos\theta & -\sin\theta \\ \sin\theta & \cos\theta\end{pmatrix} \\
\boldsymbol{I}_{d\times d} -
\frac{(\boldsymbol{a} - \boldsymbol{b})(\boldsymbol{a} - \boldsymbol{b})^{\top}}{1-\cos\theta},\quad &\text{当}\,\boldsymbol{R}=\begin{pmatrix}\cos\theta & \sin\theta \\ \sin\theta & -\cos\theta\end{pmatrix}
\end{aligned}\right.\label{eq:final-2}\end{equation}
值得留意的是第二个矩阵,它是一个对称的正交矩阵(正交性是必然的,对称性不是)!这就意味着同一个正交矩阵$\boldsymbol{T}$,它既可以将$\boldsymbol{a}$变为$\boldsymbol{b}$,也可以将$\boldsymbol{b}$变为$\boldsymbol{a}$:
\begin{equation}\boldsymbol{b}=\boldsymbol{T}\boldsymbol{a},\quad\boldsymbol{a}=\boldsymbol{T}\boldsymbol{b}\end{equation}
不得不说这结果相当有意思,所以我们选择它作为我们的最终答案。注意到$2(1-\cos\theta)=\Vert\boldsymbol{a} - \boldsymbol{b}\Vert^2$,所以该结果还可以写成:
\begin{equation}\boldsymbol{T} = \boldsymbol{I}_{d\times d} -
2\left(\frac{\boldsymbol{a} - \boldsymbol{b}}{\Vert\boldsymbol{a} - \boldsymbol{b}\Vert}\right)\left(\frac{\boldsymbol{a} - \boldsymbol{b}}{\Vert\boldsymbol{a} - \boldsymbol{b}\Vert}\right)^{\top}\end{equation}
这就是以$\boldsymbol{a} - \boldsymbol{b}$为镜面的Householder变换。所以如果已经熟知Householder变换,那么这个结果可以轻松推导出来。
通过如下思路,我们还可以得到形式上更加对称的$\boldsymbol{T}$:
要得到$\boldsymbol{T}$使得$\boldsymbol{b}=\boldsymbol{T}\boldsymbol{a}$,可以先寻找$\tilde{\boldsymbol{T}}$使得$-\boldsymbol{b}=\tilde{\boldsymbol{T}}\boldsymbol{a}$,然后让$\boldsymbol{T}=-\tilde{\boldsymbol{T}}$。
也就是说,在结果$\eqref{eq:final-2}$中将$\boldsymbol{b}\to -\boldsymbol{b}$,然后整体取反号,也能得到符合要求的变换。对于$\eqref{eq:final-2}$的第二个解,应用此思路我们可以得到
\begin{equation}\boldsymbol{T} =
\frac{(\boldsymbol{a} + \boldsymbol{b})(\boldsymbol{a} + \boldsymbol{b})^{\top}}{1+\cos\theta} - \boldsymbol{I}_{d\times d}=\frac{(\boldsymbol{a} + \boldsymbol{b})(\boldsymbol{a} + \boldsymbol{b})^{\top}}{1+\boldsymbol{a}^{\top}\boldsymbol{b}} - \boldsymbol{I}_{d\times d}\label{eq:final-3}\end{equation}
这是笔者认为形式上最简单的解。注意这是一个新解,一般情况下跟$\eqref{eq:final-2}$的两个解均不相等,也就是说到目前为止我们已经给出了三个可行解。
代码 #
代码的验证能使得我们对理论结果的正确性更有信息,下面是一个参考的验证代码:
#! -*- coding: utf-8 -*-
import numpy as np
def orthonormal_matrix_for_a_to_b(a, b):
"""求正交矩阵T,使得Ta与b的方向一致
"""
a = a / np.linalg.norm(a)
b = b / np.linalg.norm(b)
ab = (a + b).reshape((-1, 1))
return ab.dot(ab.T) / (1 + a.dot(b)) - np.eye(a.shape[0])
a = np.array([1, 2, 3, 4, 5])
b = np.array([9, 8, 7, 6, 5])
T = orthonormal_matrix_for_a_to_b(a, b)
assert np.allclose(T.dot(T.T), np.eye(a.shape[0])) # 验证是否正交
r = T.dot(a) / b
assert np.allclose(r, r[0]) # 验证是否平行
assert r[0] > 0 # 验证是否同向
r = T.dot(b) / a
assert np.allclose(r, r[0]) # 验证是否平行
assert r[0] > 0 # 验证是否同向
实验结果表明结果$\eqref{eq:final-3}$确实是正确的。当然,我们也可以从$\eqref{eq:final-3}$出发,通过直接计算来验证$\boldsymbol{T}\boldsymbol{T}^{\top}=\boldsymbol{I}_{d\times d}$以及$\boldsymbol{b}=\boldsymbol{T}\boldsymbol{a},\boldsymbol{a}=\boldsymbol{T}\boldsymbol{b}$,从而确保结果是正确的。
小结 #
本文跟大家一起做了一道线性代数练习题:寻找一个将一个单位向量变换到另一个单位向量的正交矩阵,最终得到了一个颇为简单和有趣的结果。这变换通常能将一些不依赖坐标系的问题简化为一个特殊情况来处理,因此颇有实用价值。
转载到请包括本文地址:https://kexue.fm/archives/8453
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Jun. 05, 2021). 《从一个单位向量变换到另一个单位向量的正交矩阵 》[Blog post]. Retrieved from https://kexue.fm/archives/8453
@online{kexuefm-8453,
title={从一个单位向量变换到另一个单位向量的正交矩阵},
author={苏剑林},
year={2021},
month={Jun},
url={\url{https://kexue.fm/archives/8453}},
}










June 5th, 2021
可以去查一下 Householder transformation.
谢谢指出,已经补充了它跟Householder变换的联系。
June 7th, 2021
苏神,两个正交基$a$和$ b-a cos \theta$后者是不是写错了,这两相乘似乎不为0
看错了,原来前面已经假设是单位向量了
June 8th, 2021
我也觉得写错了,应该是b-bcos吧?
那就是你的“觉得”出错了。
是b-acosθ a和b都是单位向量,这是重点
August 4th, 2022
(14)的几何意义呢?
September 28th, 2022
第一个解好像不是正交的,代码上没法通过,作者有验证过吗
如果你的第一个解指的是$(11)$的第一行,那么从公式可以直接验证它的正确性(我刚刚才手算完)。因此请自行检查代码。
January 12th, 2023
向量连线中垂超平面所对应的反射矩阵?
July 12th, 2025
关于 Householder 变换,实际操作时,如QR分解或SVD,存在一个镜面法向量符号选择问题,这两个超平面总是互相垂直的。2维几何意义,原始向量视为圆半径,两个镜面反射向量相当于过圆心的直径。
不是镜面法向量符号选择,是镜面反射后的向量符号。镜面是垂直的