闲聊:神经网络与深度学习
By 苏剑林 | 2015-06-06 | 99986位读者 |在所有机器学习模型之中,也许最有趣、最深刻的便是神经网络模型了。笔者也想献丑一番,说一次神经网络。当然,本文并不打算从头开始介绍神经网络,只是谈谈我对神经网络的个人理解。如果希望进一步了解神经网络与深度学习的朋友,请移步阅读下面的教程:
http://deeplearning.stanford.edu/wiki/index.php/UFLDL教程
http://blog.csdn.net/zouxy09/article/details/8775360
机器分类 #
这里以分类工作为例,数据挖掘或机器学习中,有很多分类的问题,比如讲一句话的情况进行分类,粗略点可以分类为“积极”或“消极”,精细点分为开心、生气、忧伤等;另外一个典型的分类问题是手写数字识别,也就是将图片分为10类(0,1,2,3,4,5,6,7,8,9)。因此,也产生了很多分类的模型。
分类模型本质上是在做拟合——模型其实就是一个函数(或者一簇函数),里边有一些待定的参数,根据已有的数据,确定损失函数(最常见的损失函数,就是误差平方和,不清楚的读者,可以回忆最小二乘法的过程。),然后优化损失函数到尽可能小,从而求出待定参数值。求出参数值之后,就可以用这个函数去进行一些预测。这便是分类的基本思想了,至于防止过拟合之类的,属于细节问题,在此先不作讨论。
以上思想看上去简单,但是存在两个本质性的、难以解决的问题:1、函数的自变量是什么?2、这个函数是什么?换句话说,我怎么知道哪些东西(特征)对我想要的分类工作有帮助?其次,复杂的非线性的现象无处不在,找到这些特征后,我怎么知道用哪个函数去拟合它?事实上,这两个问题至今没有很好的答案。在深度学习出现以前,模型和特征的选取,基本都是人工选择的。换句话说,机器学习领域发展了几十年,却连两个本质性的问题都没有解决!
深度学习的出现,给这两个问题的解决带来了较大的希望。深度学习的基础,便是神经网络。
神经网络 #
神经网络解决的是第二个问题:这个函数是什么。传统的模型,如线性回归、逻辑回归,基本都是我们人工指定这个函数的形式,可是非线性函数那么多,简单地给定几个现成的函数,拟合效果往往有限,而且拟合效果很大程度上取决于找到了良好的特征——也就是还没有解决的第一个问题——函数的自变量是什么。(举个例子来说,一个函数如果是$y=x^2+x$,是二次的非线性函数,那么如果用线性回归来拟合它,那么效果怎么也不会好的,可是,我定义一个新的特征(自变量)$t=x^2$,那么$y=t+x$是关于$t,x$的线性函数,这时候用线性模型就可以解决它,问题是在不知道$y$的具体形式下,怎么找到特征$t=x^2$呢?这基本靠经验和运气了。)
为了解决“这个函数是什么”的问题,可以有多种想法,比如我们已经学过了泰勒级数,知道一般的非线性函数都能通过泰勒展式逼近。于是很自然的一个想法是:为什么不用高次多项式来逼近呢?高次多项式确实是个不错的想法,可是有学过计算方法的同学大概都知道,多项式拟合的问题是在训练数据内拟合效果很好,可是测试效果不好,也就是容易出现过拟合的现象。那么,还有没有其他办法呢?有!那位神经网络的发表者说——用复合函数来拟合!
没错,神经网络就是通过多重复合函数来拟合的!而且是最简单的函数的符合——一个是线性函数;另外一个是最简单的非线性函数:二元函数$\theta(x)$
$$\theta(x)=\left\{\begin{aligned}1,&\,x\geq 0\\-1,&\,x < 0\end{aligned}\right.$$
以最简单的三层神经网络的二分类问题为例:
首先将输入特征的加权线性组合(权重为$w^{(1)}_{j,i}$),然后在隐藏层对组合的结果取一次$\theta(x)$,然后再把结果进行加权线性组合后(权重为$w^{(2)}_{k,j}$),再在输出层取一次$\theta(x)$进行输出。整个过程就是两次线性组合,两次$\theta(x)$,交叉进行。可见,整个过程一个二重复合函数:
$$\theta\left(\sum_{j} w^{(2)}_{k,j} \theta\left(\sum_{i} w^{(1)}_{j,i} x_i\right)\right)$$
其中非线性函数$\theta(x)$,被称为激活函数。接下来我们要定义损失函数,也就是要求最小值的待优化函数。然而,优化的过程涉及到求导,$\theta(x)$是离散的,没法求导,因此,通常用一些连续的激活函数来取代它,比如Sigmoid函数
$$S(x)=\frac{1}{1+e^{-kx}}$$
现在的问题是,上面所提出的模型,究竟是否具有我们想象中的强大威力?下面这段话表明了神经网络的威力
1943年,心理学家W.S.McCulloch和数理逻辑学家W.Pitts建立了上述的神经网络和及对应的数学模型,称为MP模型。他们通过MP模型提出了神经元的形式化数学描述和网络结构方法,证明了单个神经元能执行逻辑功能。要注意,能够完成逻辑功能,也就意味着能够完成当今计算机能够做的所有事情——如今的计算机也就是一系列逻辑指令的组合而已。(当然,这里有个速度的问题,在不考虑速度的情况下,MP模型确实能够完成当前计算机能够完成的所有工作。)
深度学习 #
上面提到的只是双重复合函数,读者很容易会想到,既然这条路可行,那么取三重、四重甚至更多重的复合函数,效果应该更好?没错,这就是深度学习的原始思想了。说了那么久,终于涉及到深度学习了。
神经网络,包括多重神经网络,并不是最近才发表的模型,事实上在几十年前人们就发表了这些模型,并提出了一些求解算法。那么,深度学习与之前的神经网络区别究竟在哪里呢?一些常见的回答是,深度学习一般是很多重的(具有五、六个隐藏层是很常见的),并且引入了更有效的求解算法,能够较好地解决梯度发散、收敛到局部极小等问题。但我觉得,这并非本质性的区别,笔者认为深度学习与传统神经网络的区别在于,深度学习致力于解决的是我们前面提到的第一个问题:函数的自变量是什么?
换句话说,深度学习的算法是用来发现良好的特征的,而这部分工作,以前通常都只是靠人工来选取,而且选取的效果不一定“良好”。现在,机器能够自动(无监督地)完成这个事情,实现的效果还不比人工选取的差。找到了良好的特征,甚至线性模型都可以有不错的表现。所以,才说深度学习将人工智能领域推进了一大步,称“深度学习”为目前最接近人工智能的算法。
为什么要致力于选取良好的特征?这是出于以下几个原因:
一、准确性,找到良好的特征,意味着较好地排除了干扰因素,从而使得模型的输入都是有益的,减少了冗余;
二、计算量,比如说对图片进行分类,图像是1000x1000像素的,如果直接将所有像素输入,那么就是106个特征,这些特征全部输入到深度学习模型中,模型的参数高达1012个甚至更多,求解这么多参数的模型几乎是不可能的,而找到良好的特征,就意味着只把有用的信息输入到模型中,从而减少了参数量,使得求解成为可能;
三、储存量,良好的特征算法往往还可以用来实现文件的有效压缩,降低储存量和训练时所需要的内存。
自编码器 #
深度学习如何实现以上功能呢?四个字:信息损失!
首先我们需要意识到,我们的算法不管多智能,都是为了完成某个领域的某个任务,因此可以肯定原始数据中,肯定包含了我们不需要的信息,甚至有可能不需要的信息比需要的信息还要多。如果有办法将这些不需要的信息去掉,剩下的都是有用的信息,那该多好啊!(信息损失,理想的情况下,损失的是我们不需要的信息)可能大家还没有意识到,事实上我们人脑一直都在做同样的事情,我们将那种思维过程,称之为——抽象!
没错,就是抽象,抽象就是一个信息损失的过程。比如说有一堆球,篮球、足球、排球、乒乓球等各种球都有,我们对它们的第一认识是:它们都(近似)是“球体”——到某点距离相等的点的集合!可是别忘了,这是一堆各异的球,它们的大小、颜色、制作材料等等都不一样,我们把它们认识为“球”,就相当于把大小、颜色、制作材料等信息都损失掉了,从而只留下这堆球的共同特征——外形是大致是球体。这样的一个过程,正是我们的抽象思维,也是一个信息损失的过程!
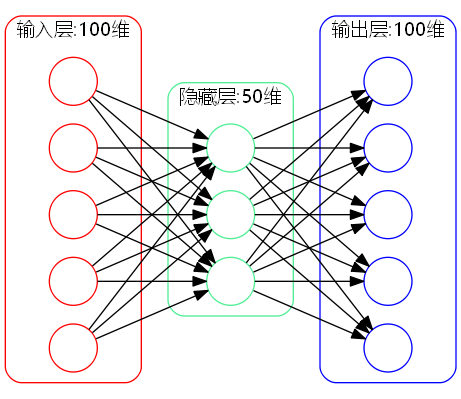
深度学习如何实现这个过程呢?“自编码器”是它的核心内容之一,它也是基于神经网络的。请读者看下面的三层神经网络:
其中网络的输入和输出是一样的(都是100维),而中间隐藏层的节点是50维的。自编码器希望通过上述神经网络,训练一个简单的函数$x=x$,也就是希望输入跟输出是一样的。可是,在训练过程中,从输入层到隐藏层,维度从100维降低到了50维,意味着信息有所损失了,可是从隐藏层到输出层,维度又恢复为100维,既然信息已经损失,因此,理论上来说这个重构过程是不可能实现的。
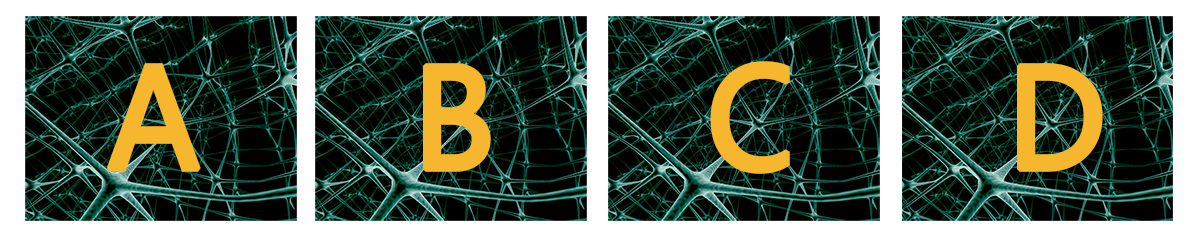
然而,我们偏要强迫它这样训练,那么会得到什么结果呢?机器也没办法,只好很勉强地从这50维数据中重构原始数据了,为了使得重构的效果尽可能好,机器只好把输入的一大批数据的共同特征提取出来,作为重构的结果。作为简单例子,请读者看以下四幅图像:
这是四幅不同的图像,读者是怎么看出它们之前的区别的呢?很显然,图片的背景都是一样的,不同的地方在于图片上面的字母,如果我要你在短时间内记住这几张图片的区别,那么读者只能够记住图片上的几个字母了。可是别忘了这是四张完整的图片,我们只记住四个字母,那就是把背景全部忽略掉了——丢失了大部分的信息!
可是如果我们的任务只是要“认出图片上的字母”,那么把背景忽略掉是完全正确的!把背景去掉后,就是我们进行判断的良好的特征,背景的存在,反而会是一种干扰。
这就是自编码的过程,也是信息损失的过程,也是抽象的过程!
总结 #
当然,深度学习的内容非常丰富,也有各种各样的变形,值得一提的是,基于深度学习的很多模型,都达到了State Of Art的效果(艺术级的,也就是最先进的),深度学习的威力可见一斑。
本文不是深度学习的入门教程,仅仅是笔者对神经网络和深度学习的一些粗浅理解,如果读者想要系统地学习相关理论,最好先阅读一些数据挖掘和机器学习的书籍,了解其中的基本概念,然后阅读文章开头提到的两篇文章。
http://ufldl.stanford.edu/wiki/UFLDL教程
http://blog.csdn.net/zouxy09/article/details/8775360
转载到请包括本文地址:https://kexue.fm/archives/3331
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Jun. 06, 2015). 《闲聊:神经网络与深度学习 》[Blog post]. Retrieved from https://kexue.fm/archives/3331
@online{kexuefm-3331,
title={闲聊:神经网络与深度学习},
author={苏剑林},
year={2015},
month={Jun},
url={\url{https://kexue.fm/archives/3331}},
}











September 22nd, 2017
打赏不多 略表心意
July 25th, 2018
多重复合函数也是能展开成多项式的形式,为什么多重复合函数的泛化能力就比多项式的好呢?
复合函数事实上可能是某个隐函数的迭代结果。而我们知道,隐函数往往比显函数更稳定、更可控。比如$y+\varepsilon\sin y = x$,可以强行用泰勒级数展开得到显式等式
$$y = x - \varepsilon \sin x + \varepsilon^2 \sin x \cos x \dots$$
也可以通过迭代
$$y_{n+1}=x-\varepsilon \sin y_n$$
得到
$$y=x - \varepsilon \sin\big (x - \varepsilon \sin (\dots)\big)$$
后者相当于神经网络,更稳定,收敛半径更大。
明白了,多谢多谢!赞!
这个解释让我很开眼界!原谅我才疏学浅知识储备不够,前者泰勒级数怎么展开的没太看懂,关于隐函数比显函数更稳定,收敛半径更大我不是很懂,也不知道为什么将隐函数写成迭代方式就可以数值求解。我应该去补哪些知识呢?
这些内容属于《数值计算》吧
June 21st, 2019
感谢博主分享
June 1st, 2020
大牛,感谢啊,写得太好了,一篇文章解释了我的很多疑问,并且环环相扣,一气呵成。牛!
July 30th, 2020
写得好!
October 25th, 2020
2020年10月25日阅读打卡
对知识的渴望永存
August 27th, 2021
每天学习,冲冲冲!
August 30th, 2021
苏神YYDS
February 17th, 2023
YYDS
June 24th, 2024
感谢博主分享!