EAE:自编码器 + BN + 最大熵 = 生成模型
By 苏剑林 | 2020-04-20 | 79968位读者 | 引用生成模型一直是笔者比较关注的主题,不管是NLP和CV的生成模型都是如此。这篇文章里,我们介绍一个新颖的生成模型,来自论文《Batch norm with entropic regularization turns deterministic autoencoders into generative models》,论文中称之为EAE(Entropic AutoEncoder)。它要做的事情给变分自编码器(VAE)基本一致,最终效果其实也差不多(略优),说它新颖并不是它生成效果有多好,而是思路上的新奇,颇有别致感。此外,借着这个机会,我们还将学习一种统计量的估计方法——$k$邻近方法,这是一种很有用的非参数估计方法。
自编码器vs生成模型
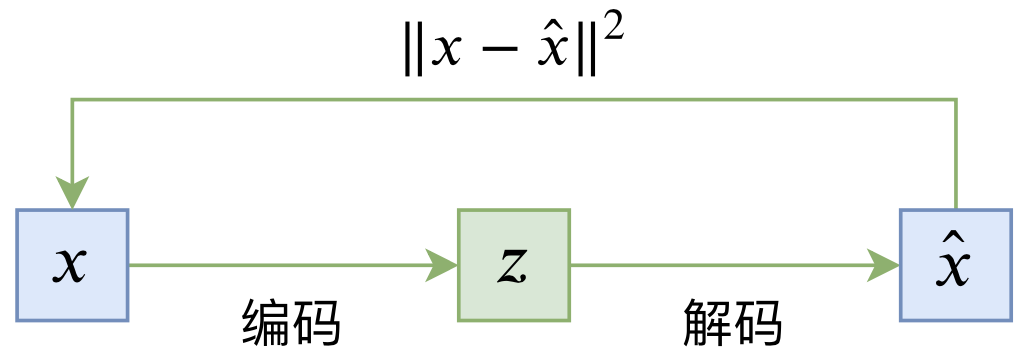
普通的自编码器是一个“编码-解码”的重构过程,如下图所示:
其loss一般为
\begin{equation}L_{AE} = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\left\Vert x - \hat{x}\right\Vert^2\right] = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\left\Vert x - D(E(x))\right\Vert^2\right]\end{equation}
深度学习的互信息:无监督提取特征
By 苏剑林 | 2018-10-02 | 361449位读者 | 引用对于NLP来说,互信息是一个非常重要的指标,它衡量了两个东西的本质相关性。本博客中也多次讨论过互信息,而我也对各种利用互信息的文章颇感兴趣。前几天在机器之心上看到了最近提出来的Deep INFOMAX模型,用最大化互信息来对图像做无监督学习,自然也颇感兴趣,研读了一番,就得到了本文。
本文整体思路源于Deep INFOMAX的原始论文,但并没有照搬原始模型,而是按照这自己的想法改动了模型(主要是先验分布部分),并且会在相应的位置进行注明。
我们要做什么
自编码器
特征提取是无监督学习中很重要且很基本的一项任务,常见形式是训练一个编码器将原始数据集编码为一个固定长度的向量。自然地,我们对这个编码器的基本要求是:保留原始数据的(尽可能多的)重要信息。
我们怎么知道编码向量保留了重要信息呢?一个很自然的想法是这个编码向量应该也要能还原出原始图片出来,所以我们还训练一个解码器,试图重构原图片,最后的loss就是原始图片和重构图片的mse。这导致了标准的自编码器的设计。后来,我们还希望编码向量的分布尽量能接近高斯分布,这就导致了变分自编码器。
重构的思考
“熵”不起:从熵、最大熵原理到最大熵模型(三)
By 苏剑林 | 2015-12-20 | 91745位读者 | 引用上集回顾
在上一篇文章中,笔者分享了自己对最大熵原理的认识,包括最大熵原理的意义、最大熵原理的求解以及一些简单而常见的最大熵原理的应用。在上一篇的文末,我们还通过最大熵原理得到了正态分布,以此来说明最大熵原理的深刻内涵和广泛意义。
本文中,笔者将介绍基于最大熵原理的模型——最大熵模型。本文以有监督的分类问题来介绍最大熵模型,所谓有监督,就是基于已经标签好的数据进行的。
事实上,第二篇文章的最大熵原理才是主要的,最大熵模型,实质上只是最大熵原理的一个延伸,或者说应用。
最大熵模型
分类:意味着什么?
在引入最大熵模型之前,我们先来多扯一点东西,谈谈分类问题意味着什么。假设我们有一批标签好的数据:
$$\begin{array}{c|cccccccc}
\hline
\text{数据}x & 1 & 2 & 3 & 4 & 5 & 6 & \dots & 100 \\
\hline
\text{标签}y & 1 & 0 & 1 & 0 & 1 & 0 & \dots & 0\\
\hline \end{array}$$
“熵”不起:从熵、最大熵原理到最大熵模型(二)
By 苏剑林 | 2015-12-11 | 111666位读者 | 引用上集回顾
在第一篇中,笔者介绍了“熵”这个概念,以及它的一些来龙去脉。熵的公式为
$$S=-\sum_x p(x)\log p(x)\tag{1}$$
或
$$S=-\int p(x)\log p(x) dx\tag{2}$$
并且在第一篇中,我们知道熵既代表了不确定性,又代表了信息量,事实上它们是同一个概念。
说完了熵这个概念,接下来要说的是“最大熵原理”。最大熵原理告诉我们,当我们想要得到一个随机事件的概率分布时,如果没有足够的信息能够完全确定这个概率分布(可能是不能确定什么分布,也可能是知道分布的类型,但是还有若干个参数没确定),那么最为“保险”的方案是选择使得熵最大的分布。
最大熵原理
承认我们的无知
很多文章在介绍最大熵原理的时候,会引用一句著名的句子——“不要把鸡蛋放在同一个篮子里”——来通俗地解释这个原理。然而,笔者窃以为这句话并没有抓住要点,并不能很好地体现最大熵原理的要义。笔者认为,对最大熵原理更恰当的解释是:承认我们的无知!
“熵”不起:从熵、最大熵原理到最大熵模型(一)
By 苏剑林 | 2015-12-01 | 107337位读者 | 引用熵的概念
作为一名物理爱好者,我一直对统计力学中“熵”这个概念感到神秘和好奇。因此,当我接触数据科学的时候,我也对最大熵模型产生了浓厚的兴趣。
熵是什么?在通俗的介绍中,熵一般有两种解释:(1)熵是不确定性的度量;(2)熵是信息的度量。看上去说的不是一回事,其实它们说的就是同一个意思。首先,熵是不确定性的度量,它衡量着我们对某个事物的“无知程度”。熵为什么又是信息的度量呢?既然熵代表了我们对事物的无知,那么当我们从“无知”到“完全认识”这个过程中,就会获得一定的信息量,我们开始越无知,那么到达“完全认识”时,获得的信息量就越大,因此,作为不确定性的度量的熵,也可以看作是信息的度量,说准确点,是我们能从中获得的最大的信息量。
新词发现的信息熵方法与实现
By 苏剑林 | 2015-10-26 | 139196位读者 | 引用在本博客的前面文章中,已经简单提到过中文文本处理与挖掘的问题了,中文数据挖掘与英语同类问题中最大的差别是,中文没有空格,如果要较好地完成语言任务,首先得分词。目前流行的分词方法都是基于词库的,然而重要的问题就来了:词库哪里来?人工可以把一些常用的词语收集到词库中,然而这却应付不了层出不穷的新词,尤其是网络新词等——而这往往是语言任务的关键地方。因此,中文语言处理很核心的一个任务就是完善新词发现算法。
新词发现说的就是不加入任何先验素材,直接从大规模的语料库中,自动发现可能成词的语言片段。前两天我去小虾的公司膜拜,并且试着加入了他们的一个开发项目中,主要任务就是网络文章处理。因此,补习了一下新词发现的算法知识,参考了Matrix67.com的文章《互联网时代的社会语言学:基于SNS的文本数据挖掘》,尤其是里边的信息熵思想,并且根据他的思路,用Python写了个简单的脚本。









最近评论