6
Jul
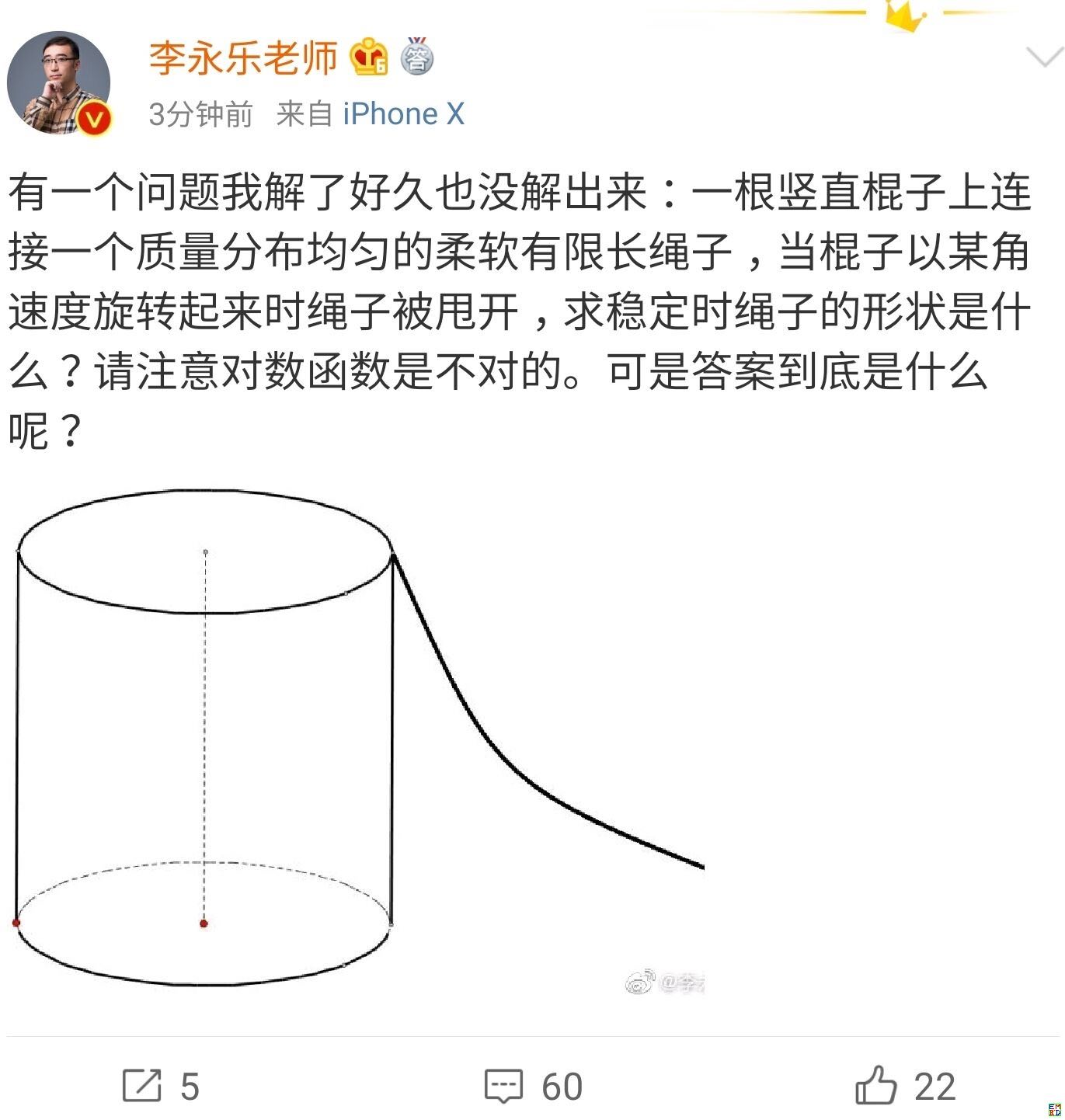
你跳绳的时候，想过绳子的形状曲线是怎样的吗？
By 苏剑林 | 2019-07-06 | 49925位读者 | 引用
28
Dec
矩阵描述三维空间旋转
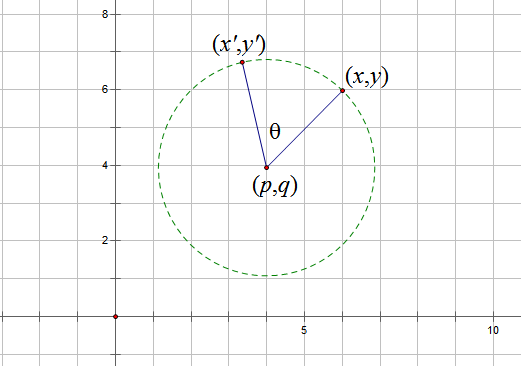
By 苏剑林 | 2013-12-28 | 89313位读者 | 引用本节简单介绍用矩阵来描述旋转。在二维平面上，复数无疑是描述旋转的最佳工具；然而推广到三维空间中，却要动用到“四元数”了。为了证明四元数的相关结论，我们需要三维旋转的矩阵描述。最一般的旋转运动为：绕某一根轴旋转$\theta$角度。这样我们就需要三个参数来描述它：确定一根轴至少需要两个参数，确定角度需要一个参数。因此，如果要用“数”来描述三维空间的伸缩和旋转的话，“三元数”显然是不够的，完成这一目的至少需要四元数。这也从另外一个角度反映了三元数的不存在性。
矩阵方法
首先我们认识到，如果旋转轴是坐标轴之一，那么旋转矩阵将是最简单的，比如向量$\boldsymbol{x}=(x_0,y_0,z_0)^{T}$绕$z$轴逆时针旋转$\theta$角后的坐标就可以描述为
$$\begin{equation}
\boldsymbol{R}_{\theta}\boldsymbol{x}\end{equation}$$
农村的孩子免不了常做家务，当然我家也没有什么特别沉重的家务，通常都是扫地、做饭、洗菜这些简单的活儿。说到洗菜，洗完菜后总喜欢边放水边搅水，然后就在水面上形成一个颇为有趣的漩涡。现在我们从数学物理的角度来分析一下这个漩涡。
在讲洗手盆的漩涡之前，我们先来看一下一个比较类似的、更古老的问题——牛顿的旋转液面问题。牛顿假设有一个水桶（假设为圆柱形吧，但这不重要），水桶在绕自己的中轴线匀角速度旋转，直到桶内的水也随着匀角速度旋转（即水与水桶相对静止），此时水的液面形状是凹的，我们来看看该液面的形状。
牛顿的水桶
要分析形状，我们还要回顾之前提到过的流体静力学平衡：
http://kexue.fm/archives/1964/
5
Apr
重提“旋转弹簧伸长”问题（变分解法）
By 苏剑林 | 2011-04-05 | 20314位读者 | 引用感谢Awank-Newton读者的来信，本文于2013.01.30作了修正，主要是弹性势能的正负号问题。之前连续犯了两个错误，导致得出了正确答案。现在已经修正。参考《平衡态公理的修正与思考》
在下面的两篇文章中，BoJone已经介绍了这个“旋转弹簧伸长”的问题，并从两个角度提供了两种解答方法。前者列出了一道积分方程，然后再转变为微分方程来解；后者直接从弹性力学的角度来列出一道二阶微分方程，两者殊途同归。
http://kexue.fm/archives/782/
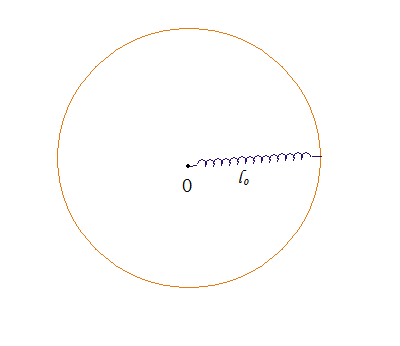
今天，再经过一段时间的变分法涉猎后，BoJone尝试从变分的角度（总能量最小）来给出一种新的解法。同样设r为旋转达到平衡后弹簧上一点到旋转中心的距离，该点的线密度为$\lambda =\lambda (r)$，该点到中心的弹簧质量为$m=m(r)$，旋转前的长度为$l_0$，旋转平衡后的长度为$l_1$。由于弹簧旋转后已经达到了平衡状态，由平衡态公理（参看《自然极值》系列），平衡意味着总能量“动能-势能”取极值。
23
Aug
《向量》系列——4.天旋地转(向量,复数,极坐标)
By 苏剑林 | 2010-08-23 | 39920位读者 | 引用
7
Aug
旋转的弹簧将如何伸长(2)？
By 苏剑林 | 2010-08-07 | 28147位读者 | 引用
30
Jul
旋转的弹簧将如何伸长？
By 苏剑林 | 2010-07-30 | 96860位读者 | 引用
26
Jul
最近评论