【备忘】维基百科与DNSCrypt
By 苏剑林 | 2015-05-30 | 45078位读者 | 引用中文维基百科的域名zh.wikipedia.org于5月19日被关键字屏蔽和DNS污染,目前从中国已无法访问中文维基百科,中文维基百科的域名也无法解析出正确的IP地址,而英文维基百科目前未受影响,可以正常访问。
【翻译】巨型望远镜:要继续,就得有牺牲!
By 苏剑林 | 2015-06-10 | 27468位读者 | 引用文章来自:新科学家,这是一篇关于30米望远镜(Thirty Meter Telescope,TMT)的新闻,起因是望远镜的制造遭到当地人的不满,当然背后的原因是很深远的,难以说清楚。更多有关TMT的新闻,可以阅读:http://www.ctmt.org/
夏威夷的巨型望远镜:要继续,就得有牺牲!
四分之一必须离开!在停止了两个月之后,夏威夷的巨型30米望远镜(Thirty Meter Telescope,TMT)重新回归到建设进程——但要牺牲其他望远镜。
由于夏威夷当地居民的抗议声越来越大,早在四月望远镜的建设工作就被迫暂停。与该望远镜相比,目前世界上所有的望远镜都相形见绌——它让能够让天文学家们凝视可见的宇宙的边缘。它位于许多夏威夷人认为是“神圣之地”的死火山莫纳克亚山,因此被夏威夷人认为是一种侮辱——尤其是在山顶已经有十多个望远镜了。
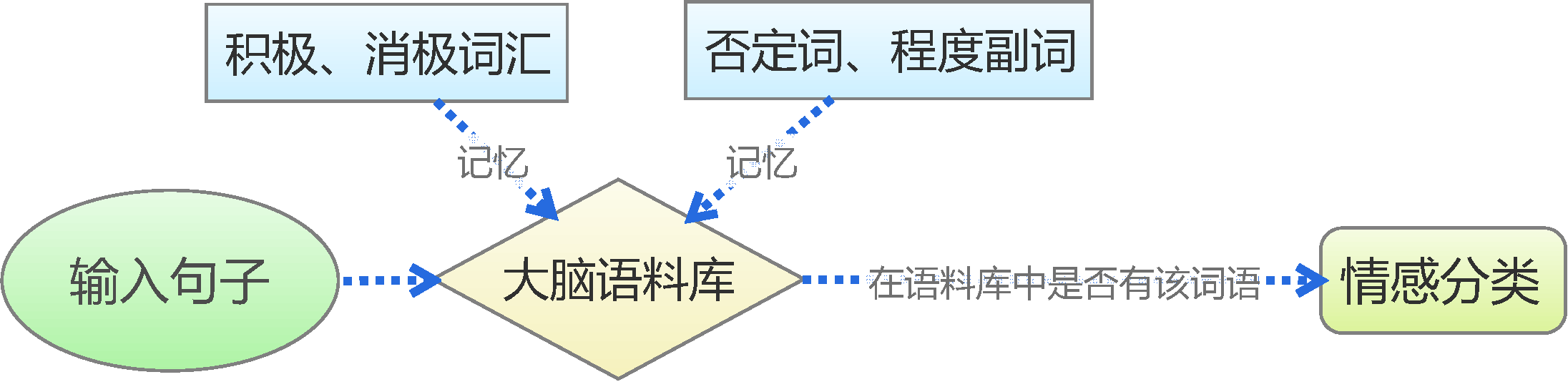
文本情感分类(一):传统模型
By 苏剑林 | 2015-06-22 | 225040位读者 | 引用前言:四五月份的时候,我参加了两个数据挖掘相关的竞赛,分别是物电学院举办的“亮剑杯”,以及第三届 “泰迪杯”全国大学生数据挖掘竞赛。很碰巧的是,两个比赛中,都有一题主要涉及到中文情感分类工作。在做“亮剑杯”的时候,由于我还是初涉,水平有限,仅仅是基于传统的思路实现了一个简单的文本情感分类模型。而在后续的“泰迪杯”中,由于学习的深入,我已经基本了解深度学习的思想,并且用深度学习的算法实现了文本情感分类模型。因此,我打算将两个不同的模型都放到博客中,供读者参考。刚入门的读者,可以从中比较两者的不同,并且了解相关思路。高手请一笑置之。
基于情感词典
文本情感分类(二):深度学习模型
By 苏剑林 | 2015-08-04 | 606510位读者 | 引用ARXIV数学论文分布:偏微分方程最热门!
By 苏剑林 | 2015-11-13 | 31468位读者 | 引用笔者成功地保研到了中山大学的基础数学专业,这个专业自然是比较理论性的,虽然如此,我还会保持着我对数据分析、计算机等方面的兴趣。这几天兴致来了,想做一下结合我的专业跟数据挖掘相结合的研究,所以就爬取了ARXIV上面近五年(2010年到2014年)的数学论文(包含的数据有:标题、分类、年份、月份),想对这几年来数学的“行情”做一下简单的分析。个人认为,ARVIX作为目前全球最大的论文预印本的电子数据库,对它的数据进行分析,所得到的结论是能够具有一定的代表性的。
当然,本文只是用来练手爬虫和基本数据分析的文章,并没有挖掘出特别有价值的信息。文末附录了笔者爬取到的数据,供有兴趣的读者进一步分析研究。
整体情况
这五年来,ARXIV的数学论文总数为135009篇,平均每年27000篇,或者每天74篇。
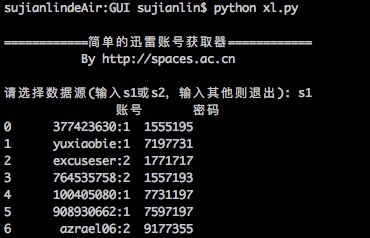
简单的迅雷VIP账号获取器(Python)
By 苏剑林 | 2016-01-20 | 32105位读者 | 引用在Windows工作的时候,经常会用迅雷下载东西,如果速度慢或者没资源,尤其是一些比较冷门的视频,迅雷的VIP会员服务总能够帮上大忙。后来无意间发现了有个“迅雷VIP账号获取器”的软件,可以获取一些临时的VIP账号供使用,这可是个好东西,因为开通迅雷会员虽然不贵,但是我又不经常下载,所以老感觉有点浪费,而有了这个之后,我随时下点东西都可以免费用了。
最近转移到了Mac上,而Mac也有迅雷,但那个账号获取器是exe的,不能在Mac运行。本以为获取器的构造会很复杂,谁知道,经过抓包研究,发现那个账号获取器的原理极其简单,说白了,就是一个简单的爬虫,以下这两个网站提供账号,它就到相应的抓取账号而已:
http://yunbo.xinjipin.com/
http://www.fenxs.com
据此,我也用Python简单写了一个,主要是方便我在Mac使用。读者如果有需要,也可以下载使用,代码兼容2.x和3.x的版本。主要的库是requests和re,pandas和sys的使用只不过是为了更加人性化。本来想用Tkinter写一个简单的GUI的,但是想想看,还是没必要了~~
年三十折腾极路由之SSH反向代理
By 苏剑林 | 2016-02-07 | 60890位读者 | 引用今天是年三十了,这里简单祝大家除夕快乐,新年快乐!愿大家在新的一年里都晋升为学神。^_^
这两天主要在折腾家里的路由器。平时家里只有爸妈两人,所以为了节省,家里只是通过中继隔壁家的网络来上网。本来家里用小米路由器mini,可是小米mini中继模式下功能限制非常多,我又不想刷第三方固件(因为这样会失去app控制功能,不是很方便),所以干脆换了个极路由3。极路由在中继模式下仍然保留了大部分功能(我觉得这样才是正常的,我不理解小米mini在中继之后就没了那么多功能究竟是什么逻辑)。
作为折腾派,一个新路由到手,总有很多东西要配置,极路由本身是基于openwrt的,因此可玩性也很强。首先要完成中继,然后上网,这个很简单就不多说了。其次是获得ssh权限,在极路由那里叫做“申请开发者模式”,或者叫root(感觉极路由想做路由界的苹果,但是在如今这个时代,苹果当初那种发展模式估计很难发展起来了),这个步骤也不难,不过申请之后就会失去极路由的保修资格(不理解这是什么逻辑)。
本文主要介绍了怎么在openwrt(极路由)上安装python,以及建立SSH反向代理(实现内网穿透)。
一个非线性差分方程的隐函数解
By 苏剑林 | 2016-04-09 | 41575位读者 | 引用问题来源
笔者经常学习的数学研发论坛曾有一帖讨论下述非线性差分方程的渐近求解:
$$a_{n+1}=a_n+\frac{1}{a_n^2},\, a_1=1$$
原帖子在这里,从这帖子中我获益良多,学习到了很多新技巧。主要思路是通过将两边立方,然后设$x_n=a_n^3$,变为等价的递推问题:
$$x_{n+1}=x_n+3+\frac{3}{x_n}+\frac{1}{x_n^2},\,x_1=1$$
然后可以通过巧妙的技巧得到渐近展开式:
$$x_n = 3n+\ln n+a+\frac{\frac{1}{3}(\ln n+a)-\frac{5}{18}}{n}+\dots$$
具体过程就不提了,读者可以自行到上述帖子学习。
然而,这种形式的解虽然精妙,但存在一些笔者不是很满意的地方:
1、解是渐近的级数,这就意味着实际上收敛半径为0;
2、是$n^{-k}$形式的解,对于较小的$n$难以计算,这都使得高精度计算变得比较困难;
3、当然,题目本来的目的是渐近计算,但是渐近分析似乎又没有必要展开那么多项;
4、里边带有了一个本来就比较难计算的极限值$a$;
5、求解过程似乎稍欠直观。
当然,上面这些缺点,有些是鸡蛋里挑骨头的。不过,也正是这些缺点,促使我寻找更好的形式的解,最终导致了这篇文章。











最近评论