构造一个显式的、总是可逆的矩阵
By 苏剑林 | 2019-03-01 | 45208位读者 | 引用从《恒等式 det(exp(A)) = exp(Tr(A)) 赏析》一文我们得到矩阵$\exp(\boldsymbol{A})$总是可逆的,它的逆就是$\exp(-\boldsymbol{A})$。问题是$\exp(\boldsymbol{A})$只是一个理论定义,单纯这样写没有什么价值,因为它要把每个$\boldsymbol{A}^n$都算出来。
有没有什么具体的例子呢?有,本文来构造一个显式的、总是可逆的矩阵。
其实思路非常简单,假设$\boldsymbol{x},\boldsymbol{y}$是两个$k$维列向量,那么$\boldsymbol{x}\boldsymbol{y}^{\top}$就是一个$k\times k$的矩阵,我们就来考虑
\begin{equation}\begin{aligned}\exp\left(\boldsymbol{x}\boldsymbol{y}^{\top}\right)=&\sum_{n=0}^{\infty}\frac{\left(\boldsymbol{x}\boldsymbol{y}^{\top}\right)^n}{n!}\\
=&\boldsymbol{I}+\boldsymbol{x}\boldsymbol{y}^{\top}+\frac{\boldsymbol{x}\boldsymbol{y}^{\top}\boldsymbol{x}\boldsymbol{y}^{\top}}{2}+\frac{\boldsymbol{x}\boldsymbol{y}^{\top}\boldsymbol{x}\boldsymbol{y}^{\top}\boldsymbol{x}\boldsymbol{y}^{\top}}{6}+\dots\end{aligned}\end{equation}
从一个单位向量变换到另一个单位向量的正交矩阵
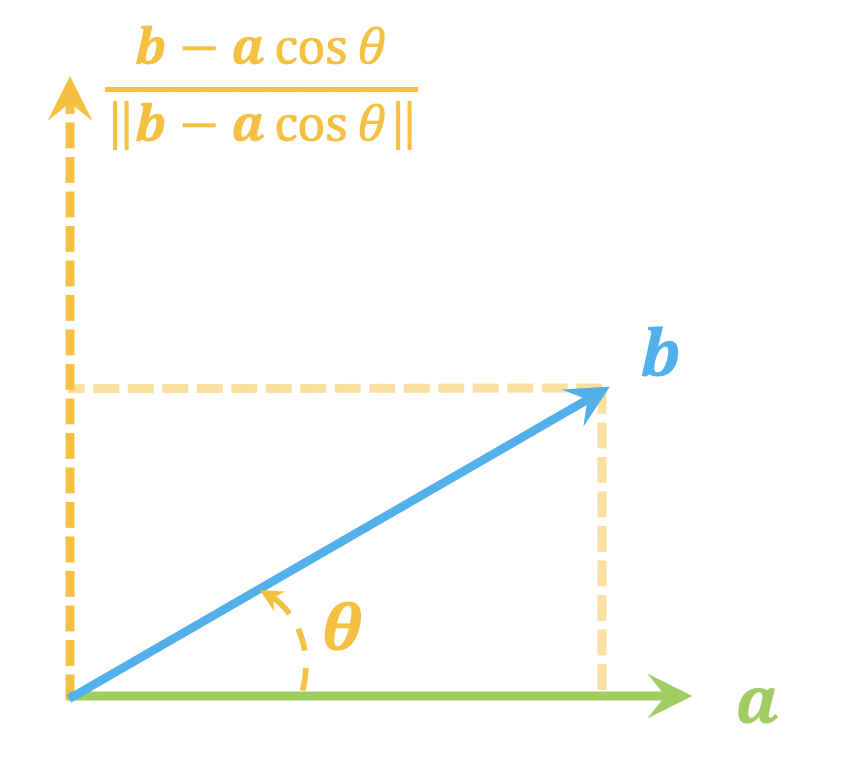
By 苏剑林 | 2021-06-05 | 46859位读者 | 引用这篇文章我们来讨论一个比较实用的线性代数问题:
给定两个$d$维单位(列)向量$\boldsymbol{a},\boldsymbol{b}$,求一个正交矩阵$\boldsymbol{T}$,使得$\boldsymbol{b}=\boldsymbol{T}\boldsymbol{a}$。
由于两个向量模长相同,所以很显然这样的正交矩阵必然存在,那么,我们怎么把它找出来呢?
二维
不难想象,这本质上就是$\boldsymbol{a},\boldsymbol{b}$构成的二维子平面下的向量变换(比如旋转或者镜面反射)问题,所以我们先考虑$d=2$的情形。
指数梯度下降 + 元学习 = 自适应学习率
By 苏剑林 | 2022-03-03 | 33387位读者 | 引用前两天刷到了Google的一篇论文《Step-size Adaptation Using Exponentiated Gradient Updates》,在其中学到了一些新的概念,所以在此记录分享一下。主要的内容有两个,一是非负优化的指数梯度下降,二是基于元学习思想的学习率调整算法,两者都颇有意思,有兴趣的读者也可以了解一下。
指数梯度下降
梯度下降大家可能听说得多了,指的是对于无约束函数$\mathcal{L}(\boldsymbol{\theta})$的最小化,我们用如下格式进行更新:
\begin{equation}\boldsymbol{\theta}_{t+1} = \boldsymbol{\theta}_t - \eta\nabla_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta}_t)\end{equation}
其中$\eta$是学习率。然而很多任务并非总是无约束的,对于最简单的非负约束,我们可以改为如下格式更新:
\begin{equation}\boldsymbol{\theta}_{t+1} = \boldsymbol{\theta}_t \odot \exp\left(- \eta\nabla_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta}_t)\right)\label{eq:egd}\end{equation}
这里的$\odot$是逐位对应相乘(Hadamard积)。容易看到,只要初始化的$\boldsymbol{\theta}_0$是非负的,那么在整个更新过程中$\boldsymbol{\theta}_t$都会保持非负,这就是用于非负约束优化的“指数梯度下降”。
GlobalPointer下的“KL散度”应该是怎样的?
By 苏剑林 | 2022-04-15 | 28127位读者 | 引用最近有读者提到想测试一下GlobalPointer与R-Drop结合的效果,但不知道GlobalPointer下的KL散度该怎么算。像R-Drop或者虚拟对抗训练这些正则化手段,里边都需要算概率分布的KL散度,但GlobalPointer的预测结果并非一个概率分布,因此无法直接进行计算。
经过一番尝试,笔者给出了一个可用的形式,并通过简单实验验证了它的可行性,遂在此介绍笔者的分析过程。
对称散度
KL散度是关于两个概率分布的函数,它是不对称的,即$KL(p\Vert q)$通常不等于$KL(q\Vert p)$,在实际应用中,我们通常使用对称化的KL散度:
\begin{equation}D(p,q) = KL(p\Vert q) + KL(q\Vert p)\end{equation}
在生活上,我是一个比较传统的人,因此每到节日我都会尽量回家跟家人团聚。也许会让大家比较吃惊的是,今年的国庆是我第一个不在家的国庆。的确,从小学到高中,上学的地方离家都比较近,每周回去一次都是不成问题的。现在来到了广州,就不能太随心了。虽然跟很多同学相比,我离家还是比较近的,但是来回也要考虑车费、时间等等。国庆假期时间虽然很长,但是中秋已经回去一趟了,所以我决定国庆就不再回去了。
对我来说,中秋跟国庆相比,中秋的意义更大些。所以我选择了国庆不回家。对家人而言,看到自己平安就好,因此哪一天回去他们都会很高兴,当然,对于农村人来说,中秋的味道更浓,更希望团聚。
哈哈,我的“《圣经》”到了
By 苏剑林 | 2013-06-27 | 57356位读者 | 引用百科翻译:草原上的狐狸(Swift Fox)
By 苏剑林 | 2009-07-07 | 38762位读者 | 引用百科翻译:臭氧的性质
By 苏剑林 | 2009-07-08 | 25081位读者 | 引用臭氧对于我们来说是极为重要的,可以说,没有臭氧,我们都会死于紫外线的强烈照射之下!这里翻译了一些关于臭氧的信息,来源于http://en.wikipedia.org/wiki/Ozone,中文维基为http://zh.wikipedia.org/w/index.php?title=%E8%87%AD%E6%B0%A7&variant=zh-cn
臭氧,英文名为Ozone或trioxygen,化学式$O_3$,每个臭氧分子含有3个氧原子,属于三原子分子。与氧气是同素异形体(组成元素相同,但是结构不同,所表现出来的性质也不同),但比氧气更不稳定。在地表上的臭氧是一种空气污染物,对人和动物的呼吸道系统会产生有害影响。而大气层上部的臭氧层则能够吸收大量的紫外线,使地球的生物不受过量紫外线的侵害。










最近评论