费曼积分法——积分符号内取微分(3)
By 苏剑林 | 2012-06-23 | 54415位读者 | 引用由于自行车之旅的原因,这篇文章被搁置了一个星期,其实应该在一个星期前就把它写好的。这篇文章继续讲讲费曼积分法的一些例子。读者或许可以从这些不同类型的例子中,发现它应用的基本方向和方法,从而提升对它的认识。
例子2:
$$\int_0^{\infty} \frac{\sin x}{x}dx$$
这也是一种比较常见的类型,它的形式为$\int \frac{f(x)}{x}dx$,对于这种形式,我们的第一感觉就是将其改写成参数形式$\int \frac{f(ax)}{x}dx$,这样的目的很简单,就是把分母给消去了,与$\int \frac{x}{f(x)}dx$的求积思想是一致的。但是深入一点研究就会发现,纵使这样能够消去分母,使得第一次积分变得简单,但是到了第二次积分的时候,我们发现,它又会变回$\int \frac{f(x)}{x}dx$的积分,使我们不能继续进行下去,因此这个取参数的方法大多数情况下都是不行的。
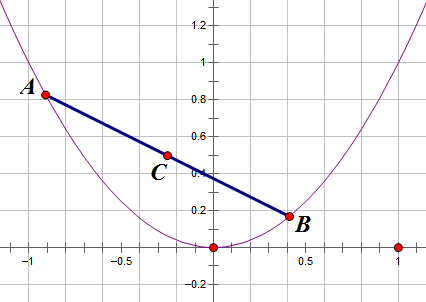
抛物线内一根定长的弦
By 苏剑林 | 2012-06-30 | 34231位读者 | 引用最近在浏览“数学研发论坛”的时候,发现了一系列不等式手册,感觉是挺宝贵的资源,就把它转载到这里来了。
当然,里边的内容难度不一,很多东西我自己也未必用得上,甚至不能弄懂,不过还是放在这里保存,并与大家分享。
原文链接:http://bbs.emath.ac.cn/thread-1549-1-1.html
文件包内容:
152个未解决的问题.pdf
HLODER 与 MINKOWSKI不等式.pdf
不等式常用证法50种.pdf
不等式基本性质.pdf
单调函数不等式.pdf
调和函数不等式.pdf
多边形与多面体不等式.pdf
反三角函数不等式.pdf
级数不等式.pdf
数论不等式.pdf
开始学习数学软件Scilab
By 苏剑林 | 2012-09-28 | 41911位读者 | 引用其实很早之前我就想学习一款数学软件的使用,以前很感兴趣的是mathematica,也玩弄过一阵子,但毕竟在高中没有多大需要,也就没有坚持下来。更重要的是,这些软件都是要收费的。上了大学后,听了师兄姐对数学建模的讲述,发现他们基本上也是用mathematica或者matlab的,但这两个软件都是要收费的,我不大想用破解版本。既然我都已经用上了ubuntu了,那么我就该好好利用它。据说命令跟matlab很相似的软件是scilab,还有octave,不同的是这些都是开源免费的。
出于熟悉代码操作和数学软件编程的目的,我选择了学习scilab。虽然网上说octave与matlab的相似程度更高,但是我感觉scilab比octave用的更广一些,所以就用它。所谓“一理通百理明”,先专心学好一个。
下面是我编写的第一个scialb程序,利用威尔逊方法来进行素性测试。这个代码的主要目的是练习条件语句和循环语句,以及一些输出输入的技巧而已。程序本身比较丑陋。
//我的第一个scilab程序
//完成于2012.09.27
label1=['p:';]; //定义标签
B=x_mdialog(['本程序使用威尔逊方法判断进行素数测试。';'请输入要判断的数'],label1,['127';]); //输入框
p=evstr(B(1)); //提取输入框里边的数字进行赋值
i=1;
j=1;
q=p-1;
while i<q
j=j*i;
j=modulo(j,p);//这个是模函数。
i=i+1;
end
if j==1
messagebox(['这是一个素数';],['测试结果']); //输出,其中后边的“测试结果”是输入框的标题
else
messagebox(['这是一个合数';],['测试结果']);
end
《新理解矩阵3》:行列式的点滴
By 苏剑林 | 2012-11-04 | 43232位读者 | 引用本文的最新版本位于:http://kexue.fm/archives/2208/
亲爱的读者朋友们,科学空间版的理解矩阵已经来到了BoJone认为是最激动人心的部分了,那就是关于行列式的叙述。这部分内容没有在孟岩的文章中被谈及到,是我自己结合了一些书籍和网络资源而得出的一些看法。其中最主要的书籍是《数学桥》,而追本溯源,促进我研究这方面的内容的是matrix67的那篇《教材应该怎么写》。本文包含了相当多的直观理解内容,在我看来,这部分内容也许不是正统的观点,但是至少在某种程度上能够促进我们对线性代数的理解。
大多数线性代数引入行列式的方式都是通过讲解线性方程组的,这种方式能够让学生很快地掌握它的计算,以及给出了一个最实际的应用(就是解方程组啦)。但是这很容易让读者走进一个误区,让他们认为线性代数就是研究解方程组的。这样并不能让读者真正理解到它的本质,而只有当我们对它有了一个直观熟练的感觉,我们才能很好地运用它。
行列式的出现其实是为了判断一个矩阵是否可逆的,它通过某些方式构造出一个“相对简单”的函数来达到这个目的,这个函数就是矩阵的行列式。让我们来反思一下,矩阵可逆意味着什么呢?之前已经提到过,矩阵是从一个点到另外一个点的变换,那么逆矩阵很显然就是为了把它变换回来。我们还说过,“运动是相对的”,点的变换又可以用坐标系的变换来实现。但是,按照我们的直觉,不同的坐标系除了有那些运算上的复杂度不同(比如一般的仿射坐标系计算点积比直角坐标系复杂)之外,不应该有其他的不同了,用物理的语言说,就是一切坐标系都是平权的。那么给出一个坐标系,可以自然地变换到另外一个坐标系,也可以自然地将它变换回来。既然矩阵是这种坐标系的一个描述,那么矩阵不可逆的唯一可能性就是:
这个$n$阶矩阵的$n$个列向量根本就构不成一个$n$维空间的坐标系。
[问题解答]有多少位数字?
By 苏剑林 | 2013-02-21 | 16656位读者 | 引用解决完上一题《有多少个5?》后,子瑞表示看到一道类似的题目,当然,这道题比上一道难一些:
一个数,各个数字加起来等于900,乘以2后各个数字加起来还是等于900,已知这个数字只有3、4、5、6组成,请问满足条件的最大数与最小数的积有多少位数?
要解答这个问题,我们只需要知道最大数和最小数分别有多少位即可。因为最大数必然是6...3的形式,而最小数只能是3...6的形式,它们的位数之和就是所求的位数。
怎样比较两个数的大小呢?显然,在不同位数的数时,位数多的数要大,同样位数才从高到低逐位比较。因此,我们应当考虑位数的最大与最小。
这已经是去年写的稿件了,刊登在今年二月份的《天文爱好者》上,本文的标题还登载了该期天爱的封面上,当时甚是高兴呢!在此与大家分享、共勉。
相信许多天文爱好者都知道第一、第二、第三宇宙速度的概念,也会有不少的天爱自己动手计算过它们。我们道,只要发射速度达到7.9km/s,宇宙飞船就可以绕地球运行了;超过11.2km/s,就可以抛开地球,成为太阳系的一颗“人造行星”;再大一点,超过16.7km/s,那么就连太阳也甩掉了,直奔深空。
16.7km/s,咋看上去并不大,因为地球绕太阳运行的速度已经是30km/s了,这个速度在宇宙中实在是太普通了。但是对于我们目前的技术来说,它大得有点可怕。维基百科上的资料显示,史上最强劲的火箭土星五号在运送阿波罗11号到月球时,飞船最终也只能加速到接近逃逸速度,即11.2km/s,而事实上第三宇宙速度已经是是目前人造飞行器的速度极限了。可是没有速度,我们就不能发射探测器去探索深空,那些科幻小说中的“星际移民”,就永远只能停留在小说上了。
正项级数敛散性最有力的判别法?
By 苏剑林 | 2013-05-17 | 101627位读者 | 引用在学习正项级数的时候,我们的数学分析教材提供了各种判别法,比如积分判别法、比较判别法,并由此衍生出了根植法、比值法等,在最后提供了一个比较精细的“Raabe判别法”。这些方法的精度(强度)各不相同,一般认为“Raabe判别法”的应用范围最广的。但是在我看来,基于p级数的比较判别法已经可以用于所有题目了,它才是最强的方法。
p级数就是我们熟悉的
$$\sum_{n=1}^{\infty} \frac{1}{n^p}$$
通过积分判别法可以得到当p>1时该级数收敛,反之发散。虽然我不能证明,但是我觉得以下结论是成立的:
若正项级数$\sum_{n=1}^{\infty} a_n$收敛,则总可以找到一个常数A以及一个大于1的常数p,使每项都有$a_n < \frac{A}{n^p}$。








最近评论