从费马大定理谈起(八):艾森斯坦整数
By 苏剑林 | 2014-08-30 | 44341位读者 | 引用是时候向n=3进军了,为了证明这个情况,我们需要一个新的数环:艾森斯坦整数(Eisenstein Integer)。艾森斯坦是德国著名数学家,同时代的高斯曾经评价:“只有三个划时代的数学家:阿基米德,牛顿和艾森斯坦。”足见艾森斯坦的成就斐然。事实上,阅读费马大定理的研究史,同时也是在阅读数学名人录——没有超高的数学,几乎不可能在费马大定理中有所建树。
基本定义
跟高斯整数一样,艾森斯坦整数也是复整数的一种,其中,高斯整数是以1和$i$为基,$i$其实是一个四次单位根,也就是$x^4-1=0$的一个非实数根,因此高斯整数也叫做四次分圆整数;而艾森斯坦整数以1和$\omega$为基,$\omega$是三次单位根,也就是$x^3-1=0$的一个非实数根。任意一个艾森斯坦整数都可以记为$a+b\omega,\,a,b\in\mathbb{Z}$,艾森斯坦整数环记为$\mathbb{Z}[\omega]$,也称为三次分圆整数环。
Cantor-Bernstein 定理(给出双射!)
By 苏剑林 | 2014-09-19 | 51822位读者 | 引用在数学分析的级数理论中,有一类常见的题目,其中涉及到
$$\cos\theta+\cos 2\theta+\dots+\cos n\theta\tag{1}$$
和
$$\sin\theta+\sin 2\theta+\dots+\sin n\theta\tag{2}$$
之类的正弦或者余弦级数的求和,主要是证明该和式有界。而为了证明这一点,通常是把和式的通项求出来。当然,该级数在物理中也有重要作用,它表示$n$个相同振子的合振幅。在我们的数学分析教材中,通常是将级数乘上一项$\sin\frac{\theta}{2}$,然后利用积化和差公式完成。诚然,如果仅限在实数范围内考虑,这有可能是唯一的推导技巧的。但是这样推导的运算过程本身不简单,而且也不利于记忆,在大二的时候我就为此感到很痛苦。前几天在看费曼的书的时候,想到了一种利用复数的推导技巧。很奇怪,这个技巧是如此简单——写出来显得这篇文章都有点水了——可是我以前居然一直没留意到!看来功力尚浅,需多多修炼呀。
有趣的求极限题:随心所欲的放缩
By 苏剑林 | 2015-03-28 | 47372位读者 | 引用昨天一好友问我以下题目,求证:
$$\lim_{n\to\infty} \frac{1^n + 2^n +\dots + n^n}{n^n}=\frac{e}{e-1}$$
将解答过程简单记录一下。
求解
首先可以注意到,当$n$充分大时,
$$\frac{1^n + 2^n +\dots + n^n}{n^n}=\left(\frac{1}{n}\right)^n+\left(\frac{2}{n}\right)^n+\dots+\left(\frac{n}{n}\right)^n$$
的主要项都集中在最后面那几项,因此,可以把它倒过来计算
$$\begin{aligned}\frac{1^n + 2^n +\dots + n^n}{n^n}=&\left(\frac{1}{n}\right)^n+\left(\frac{2}{n}\right)^n+\dots+\left(\frac{n}{n}\right)^n\\
=&\left(\frac{n}{n}\right)^n+\dots+\left(\frac{2}{n}\right)^n+\left(\frac{1}{n}\right)^n\end{aligned}$$
海伦公式的一个别致的物理推导
By 苏剑林 | 2015-03-27 | 54651位读者 | 引用海伦公式是已知三角形三边的长度$a,b,c$来求面积$S$的公式,是一个相当漂亮的公式,它不算复杂,同时它关于$a,b,c$是对称的,充分体现了三边的同等地位。可是,这样具有对称美的公式推导,往往要经过一个不对称的过程,比如维基百科上的证明,这未免有点美中不足。本文的目的,就是想为此补充一个对称的推导。本文题目为“物理推导”,关键在于“推导”而不是“证明”,同时这里的“物理”并非是通过物理类比而来,而是推导的思想和方法很具有“物理味道”。
$$\sqrt{p(p-a)(p-b)(p-c)}$$
在推导开始之前,笔者给出一个评论:海伦公式似乎是由三边长求三角形面积的所有可能的公式之中最简单的一个。
2015诺贝尔医学奖:中国人在内
By 苏剑林 | 2015-10-05 | 25253位读者 | 引用运动相机测试:家乡的星空
By 苏剑林 | 2016-08-03 | 40219位读者 | 引用记得很早之前就想尝试一下拍星空,无奈一直都没有设备。以前只知道单反可以拍星空,因此,一直以来的想法就是有钱了就去买台单反。因为各种原因一拖再拖,最后慢慢觉得,对于我这种三分钟热度的人来说,单反的意义还真的不是很大。
这两年,在小米的鼓吹下,小蚁运动相机在国内算是慢慢掀起了一股运动相机潮。这种相机的特点是小巧、灵活,价格也不贵(相比单反)。灵活不仅仅是说它便于携带,而且还是功能上的灵活,比如一代小蚁还支持编程拍摄!(写程序控制快门、ISO、拍摄间隔,并实现定时拍摄等)这样当然很快就吸引了我,在小蚁2代众筹之时,我也咬咬牙,入了一台。
前两天回到家,刚好晴夜,马上就试了一下拍星空的效果。下面是在我家楼顶拍的,用ISO400曝光30秒的效果:
简单的迅雷VIP账号获取器(Python)
By 苏剑林 | 2016-01-20 | 34065位读者 | 引用在Windows工作的时候,经常会用迅雷下载东西,如果速度慢或者没资源,尤其是一些比较冷门的视频,迅雷的VIP会员服务总能够帮上大忙。后来无意间发现了有个“迅雷VIP账号获取器”的软件,可以获取一些临时的VIP账号供使用,这可是个好东西,因为开通迅雷会员虽然不贵,但是我又不经常下载,所以老感觉有点浪费,而有了这个之后,我随时下点东西都可以免费用了。
最近转移到了Mac上,而Mac也有迅雷,但那个账号获取器是exe的,不能在Mac运行。本以为获取器的构造会很复杂,谁知道,经过抓包研究,发现那个账号获取器的原理极其简单,说白了,就是一个简单的爬虫,以下这两个网站提供账号,它就到相应的抓取账号而已:
http://yunbo.xinjipin.com/
http://www.fenxs.com
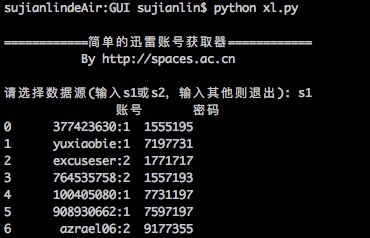
据此,我也用Python简单写了一个,主要是方便我在Mac使用。读者如果有需要,也可以下载使用,代码兼容2.x和3.x的版本。主要的库是requests和re,pandas和sys的使用只不过是为了更加人性化。本来想用Tkinter写一个简单的GUI的,但是想想看,还是没必要了~~











最近评论