今天上体育课的时候，BoJone与同学们正兴致勃勃地打着篮球，不料临近下课之时，同学猛一击（当然只是无意摩擦，没有恶意），我感到一阵猛疼——眼角处的肉破裂了！开始的一分钟内不停流血，奇怪的是到了校医室之后血就止住了（还没有经过任何处理，只是一直按住）。本以为只是小伤，简单处理就好，谁知校医说需要到外边的医院缝针，否则可能留疤毁容！！
既然如此严重，无奈只能服从了，简单处理伤口后就和母亲一起到了医院，缝了两针。由于接下来两天都得去医院消毒清洗伤口，所以干脆就请假回家了，周一再上学吧（貌似我在学校也仅仅是自学，没有多大区别^_^）...不过从受伤到现在，我还没有机会看到我的伤口究竟咋样...
26
Dec
《自然极值》系列——7.悬链线问题
By 苏剑林 | 2010-12-26 | 78964位读者 | 引用
约翰与他同时代的110位学者有通信联系，进行学术讨论的信件约有2500封，其中许多已成为珍贵的科学史文献，例如同他的哥哥雅各布以及莱布尼茨、惠更斯等人关于悬链线、最速降线（即旋轮线）和等周问题的通信讨论，虽然相互争论不断，特别是约翰和雅各布互相指责过于尖刻，使兄弟之间时常造成不快，但争论无疑会促进科学的发展，最速降线问题就导致了变分法的诞生。
有意思的是,1690年约翰·伯努利的哥哥雅可比·伯努利曾提出过悬链线问题向数学界征求答案。即：
固定项链的两端，在重力场中让它自然垂下，求项链的曲线方程.
吊桥上方的悬垂钢索，挂着水珠的蜘蛛网，电杆间的电线都是悬链线。伽利略最早注意到悬链线，猜测悬链线是抛物线。1691年莱布尼兹、惠更斯以及约翰·伯努利各自得到正确答案，所用方法是诞生不久的微积分。
The Astroncial Events Of 2010
1月1日月偏食，2：51初亏，3：23食甚，3：54复圆。食分0.082。
1月3日 火星合月
1月4日 象限仪流星雨极大
1月5日 水星下合日
1月6日 16时土星合月
1月12日 金星上合日
1月15日 日环食，我国各地从15时-15时30分初亏，云南，四川，重庆，湖北，河南，山东的部分地区可见环食。1时土星留，变为逆行。
1月16日 水星留，变为顺行。金星合月。
1月25日 19时月掩昴星团
1月27日 水星西大距
1月29日 19时42分火星冲日。-1.32等
1月30日 9时火星合月
9
Jan
不可能事件——一道经典电磁感应题的错误
By 苏剑林 | 2011-01-09 | 46139位读者 | 引用
28
May
科学空间：2011年6月重要天象
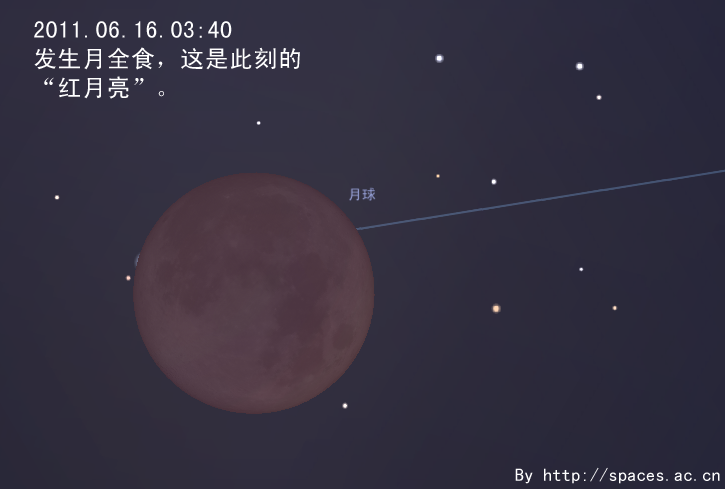
By 苏剑林 | 2011-05-28 | 28817位读者 | 引用
月全食-201106160340
6月中下旬，是北半球一年中黑夜最短的时期。今年6月22日是夏至节气，以北纬40°地区为例，当天天文昏影终到次日天文晨光始的间隔只有不到4小时50分钟。黑夜短暂会使我们可用于天文观测的时间缩短。但在夏至前后，午夜时分太阳也会在地平线下不太低的位置，这样我们就有可能整夜观测到一些类似国际空间站这样的低轨道人造天体。有兴趣的朋友可以查询相关的过境预报，挑战在一晚可以观测到多少次国际空间站过境这类的观测项目。发生在六月的日偏食和月全食，是今年天象的重头戏。接下来笔者就日偏食讲起，跟大家聊聊发生在6月的天象。
19
Feb
《方程与宇宙》:一种有趣的三体问题坐标
By 苏剑林 | 2011-02-19 | 25033位读者 | 引用通常来说，选取惯性系为参考系，列出的三体问题方程为
$$\ddot{\vec{r}}_k=\sum_{i=1,i != k}^{n} Gm_i\frac{\vec{r}_i-\vec{r}_k}{|\vec{r}_i-\vec{r}_k|^3}$$
历史上出现过很多不同形式的变换，使得三体问题的运动方程有了各样的形式，如Lagrange形式、Jacobi形式、Hamilton形式等。这些变换形式都各有特点，都能够在一定程度上化简三体问题。BoJone在研究摆弄等质量型三体问题的运动方程时，也发现了一种很有趣的变换，在此贴出与大家分享。
设$\vec{R}_1=\vec{r}_1-\vec{r}_2,\vec{R}_2=\vec{r}_2-\vec{r}_3,\vec{R}_3=\vec{r}_3-\vec{r}_1$，则三体问题的运动方程变为
最近评论