宇宙驿站定于本周五更换服务器
By 苏剑林 | 2010-07-21 | 15668位读者 | 引用《向量》系列——3.当天体力学遇到向量(1)
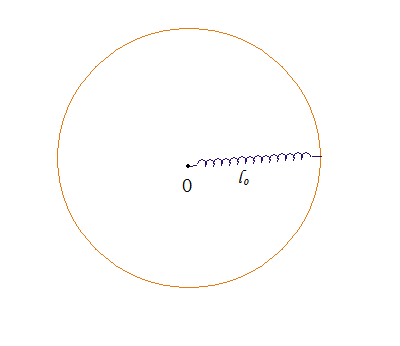
By 苏剑林 | 2010-07-24 | 17187位读者 | 引用旋转的弹簧将如何伸长?
By 苏剑林 | 2010-07-30 | 104636位读者 | 引用科学空间:2010年8月重要天象
By 苏剑林 | 2010-08-02 | 27966位读者 | 引用旋转的弹簧将如何伸长(2)?
By 苏剑林 | 2010-08-07 | 30043位读者 | 引用谈谈“民科”——兼谈如何推翻爱恩斯坦?
By 苏剑林 | 2010-08-11 | 159405位读者 | 引用民科,是“平民科学家”的简称,本来,无论怎么看,这个词都是一个褒义词,代表了一群默默进行科学研究的人,本来,我等天文爱好者都可以用上“民科”这一漂亮词语。然而,“得益于”某些民科(至少在中国是这样的)的狂妄自大,使得“民科”成为了另外一群人的代名词。他们他们从最基础的物理学比如牛顿力学开始,就和正统的物理学分道扬镳。他们使用的专业术语跟正统的物理学都不同。你说东,他说西,以致于民科和专业人士完全不能交流。还有一些民科从易经八卦这些所谓的哲学原理出发,提出一些自以为是的邪乎学说,完全不在物理学的轨道上。这一群人,仿佛自认为自己是救世主,他们就是崭新而又来源已久的新“民科”。由此看,民科和物理学之间存在一个无法沟通的真空。
今天我们都是舟曲人——举国哀悼舟曲遇难同胞
By 苏剑林 | 2010-08-14 | 24269位读者 | 引用《方程与宇宙》:拉格朗日点,复数,向量(五)
By 苏剑林 | 2010-08-16 | 56361位读者 | 引用The New Calculation Of Lagrangian Point 4,5
上一回我们已经求出了拉格朗日点L1,L2,L3,并且希望能够求出L4,L5两个点。由于L4,L5与“地球-太阳”连线已经不共线了,所以前边的方法貌似不能够用了。为了得到一个通用的定义,我们可以采用以下方法来描述拉格朗日点:位于拉格朗日点的天体,它与太阳的连线以及地球与太阳的连线所组成的角的大小是恒定的。(这里为了方便,采用了地日系的拉格朗日点来描述,对于一般的三体问题是一样的)
对于L4,L5来说,我们或许可以设置一个新的向量来描述这两点的向径(如$\vec{R}$)。当我们这样做后,很快就会发现这样会令我们的计算走向死胡同。因为我们发现:已知两个向量的夹角和其中一个向量,我们很难把另一个向量用已知向量的式子表达出来。不能做到这一点,就不能找出$\vec{R}$与$\vec{r}$的关系,就无法联立方程求解。难道,我们这一条路走到尽头了吗?一开始BoJone也冥思苦想不得头绪,但是...












最近评论