15
May
地球引力场的悬链线方程
By 苏剑林 | 2011-05-15 | 60347位读者 | 引用之前曾在《自然极值》系列文章中提到过均匀重力场下的悬链线形状问题，并且在那文章中向读者提出：在一个质点（地球）引力场中的悬链线形状会是怎么样的。说实话，提出这个问题的时候，我还不懂怎么解答这个问题，不过现在会了，回头一看，已经几个月了，时间过得真快...
与之前的思路一样，我们依旧采用的是“平衡态公理”，即总势能最小。从天体力学中我们知道，任意两个质点间的势能为$-\frac{Gm_1 m_2}{r}$。对于本题的悬链线问题，我们可以把地球放到坐标原点位置，而悬链的两个固定点分别为$(x_1,y_1)$和$(x_2,y_2)$，链的总长度为l。即
$$\int_{x_1}^{x_2} \sqrt{dx^2+dy^2}=l$$
19
Jun
向量结合复数：常曲率曲线(1)
By 苏剑林 | 2011-06-19 | 29371位读者 | 引用在之前的一篇向量系列的文章中，我们通过结合物理与向量来巧妙地推导出了曲线（包括平面和空间的）的曲率半径为
$$R=\frac{v^2}{a_c}=\frac{|\dot{\vec{r}}|^3}{|\dot{\vec{r}}\times \ddot{\vec{r}}|}\tag{1}$$
曲率则是曲率半径的导数：$\rho=\frac{1}{R}$。我们反过来思考一下：曲率恒定的平面曲线是否只有圆？
答案貌似是很显然的，我们需要证明一下。
由于只是考虑平面情况，我们先设$\dot{\vec{r}}=(v cos\theta,v sin\theta)=z=ve^{i\theta}$，代入(1)得到
$\frac{\dot{\theta}}{v}=\rho$————(2)
19
Jul
一道整数边三角形题目
By 苏剑林 | 2011-07-19 | 21183位读者 | 引用
27
Jul
科学空间：2011年8月重要天象
By 苏剑林 | 2011-07-27 | 17327位读者 | 引用
26
Jun
费曼积分法——积分符号内取微分(4)
By 苏剑林 | 2012-06-26 | 72075位读者 | 引用趁着早上有空，就赶紧把这篇文章写好吧。下午高考成绩要公布了，公布后也许又会有一段时间忙碌了。这应该是“费曼积分法”系列最后一篇文章了。它主要讲的还是费曼积分法的一个实例。不同的是，这是BoJone首次独立地用费曼积分法解决了一个问题。之前提到的一些例子，都是书本提供并结合了提示，BoJone才把它们算出来的。所以这个问题有着点点纪念意义。
数学研发论坛上wayne曾求证这样的命题：
$\int_0^{\infty}\frac{f(x,2m-1)-\sin x}{x^{2m+1}}dx$其中，f(x,2m-1)表示sinx的2m-1阶泰勒展开
如m=1时，
$$\int_0^{\infty}\frac{x-\sin x}{x^3}dx$$
m=2时
$$\int_0^{\infty}\frac{x-\frac{x^3}{6}-\sin x}{x^5}dx$$
借助软件我发现结果是：
$\frac{\pi(-1)^{m-1}}{2(2m)!}$
6
Jul
椭圆内的一根定长弦（化圆法）
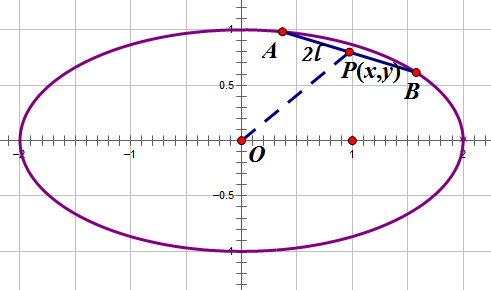
By 苏剑林 | 2012-07-06 | 30691位读者 | 引用在上一篇文章《抛物线内的一根定长弦》中，我们解决了抛物线内的定长弦中点轨迹问题，那还算是一个比较简单的问题。虽然同是圆锥曲线，但把同样的问题延伸到椭圆上，却不是那么简单了。因为椭圆的轨迹方程的x,y坐标通过平方相互“纠缠”在一起，不像抛物线方程那样可以容易分离开来（指的是分离成$y=f(x)$的形式）。BoJone尝试了若干种方法，还是难以把它的轨迹求出来。最后通过“化圆法”，终得轨迹方程。
椭圆内的定长弦1
所谓化圆法，就是将椭圆通过拉伸变成一个圆，利用圆的性质来解决一些问题。众所周知，相比椭圆，圆具有相当多的简单性。这是我高考前研究各种各样的高考圆锥曲线题时，所总结出来的一种方法。有时候，把椭圆拉伸为圆后，结论就相当显然了；同时，圆作为一个特殊的椭圆，椭圆的一般结论，放在圆上自然也是成立的。所以要研究椭圆问题，不妨先研究它的特例——圆问题；另一方面，利用圆的对称性等等，也可以大幅度地减少计算量，所以BoJone很喜欢这个方法。更想不到的是，它居然在求本文的轨迹时派上用场了。
最近在浏览“数学研发论坛”的时候，发现了一系列不等式手册，感觉是挺宝贵的资源，就把它转载到这里来了。
当然，里边的内容难度不一，很多东西我自己也未必用得上，甚至不能弄懂，不过还是放在这里保存，并与大家分享。
原文链接：http://bbs.emath.ac.cn/thread-1549-1-1.html
文件包内容：
152个未解决的问题.pdf
HLODER 与 MINKOWSKI不等式.pdf
不等式常用证法50种.pdf
不等式基本性质.pdf
单调函数不等式.pdf
调和函数不等式.pdf
多边形与多面体不等式.pdf
反三角函数不等式.pdf
级数不等式.pdf
数论不等式.pdf
30
Aug
折腾windows 8和ubuntu 12
By 苏剑林 | 2012-08-30 | 20635位读者 | 引用这是一篇用Windows 8完成的文章。
快开学了，华师2号就要报道了，所以就提前入手一台手提电脑，联想Z575AM-ASI，四千元的AMD，4核，64位机器。
我的台式机已经是六年前的产品了，联想的家悦系列，只有512MB内存。所以相比之下，这新机器配置还过得去吧，对于CPU，我个人还是倾向于AMD的，因为我的那台家悦台式也是AMD的CPU，所以对它很有好感。新兴的联想专卖店没有AMD手提，所以还得提前向他们预订。
Windows8
手提本身没有预装操作系统，专卖店很随手地为我装了一个win7，而且还只是ghost版本的，时不时会卡死，感觉很不好，刚好前些日子在网上开始发布Windows8了，所以就马上把Win7格掉，装上Windows8了。安装过程很顺利，由于还没有正式发布，所以还没有激活，这段时间纯粹体验中。等正式版发布了，再计划买一个正版光盘吧
最近评论