科学空间|Scientific Spaces

圆锥曲线

经过上两回的讨论，我们已经基本摸清了二体问题的运动情况。我们已经找到了二体问题在轨道为椭圆的时候的所有积分，给出了“活力公式”等常用公式的证明，并且留下了一些没有解答的问题。那就是在轨道为抛物线和双曲线时的最后一个积分还没有找出来，现在我们解决这两个问题。其中的关键积分依旧是
$\dot{r}^2={2\mu}/r-{\mu a(1-e^2)}/r^2-\frac{\mu}{a}$——(12)

点击阅读全文...

信使号的水星假色影像（维基百科）

进入4月，我们的天象剧场又逐渐热闹起来。9日的水星东大距，是全年水星为数不多的较佳观测时机之一。4月下旬天琴座流星雨也将如约而至，它的到来会使天文爱好者们的春夜观星计划更加丰富多彩。本月，火星、水星、土星，都是星空的主角！

点击阅读全文...

二体运动

在上一回的讨论中，我们已经解决了大部分的问题，并且表达了找到r或者$\theta$关于时间t的函数的希望。在最后的内容中，我们做了以下工作：

由(7)得到$\dot{\theta}=h/r^2$，代入(6)得到：
$$\ddot{r} -h^2/r^3=-\frac{\mu}{r^2}\tag{10}$$这是一个二阶微分方程，它的解很容易找出，但是这个积分太复杂：
$$\dot{r}\frac{d\dot{r}}{dr}=h^2/r^3-\frac{\mu}{r^2}$$
$\dot{r}d\dot{r}=(h^2/r^3-\frac{\mu}{r^2})dr$，两端积分
$$\dot{r}^2={2\mu}/r-h^2/r^2+K_1\tag{11}$$$$\Rightarrow {dt}/{dr}=\frac{r}{\sqrt{K_1 r^2+2\mu r-h^2}}$$
$t=\int \frac{r}{\sqrt{K_1 r^2+2\mu r-h^2}}dr$

点击阅读全文...

二体问题的轨道模拟

为了让大家能够查询到“天体力学”方面的内容，同时锻炼我的表达和计算能力，BoJone构思了《方程与宇宙》这个主题，主要是写一些关于使用数学相对深入地讨论一些天文问题。其实我一直觉得，不用公式是无法完美地描述科学的（当然也不能纯公式），我记得霍金的《时间简史》以及《果壳中的宇宙》等之类的书，都力求不用或者尽可能少用数学公式来表达自己的观点。这种模式对于对于公众来说是很好的，但是对于希望深入研究的朋友来说却难以进行。所以我主张：宇宙是算出来的！

这个主题每一个字都是由BoJone敲击出来的，其中包括引用了《天体力学引论》里面的一些内容，以及加入了BoJone个人的一些见解。由于篇幅长及时间有限问题，BoJone打算分若干次撰写发布，并且尽可能写得通俗一点，力求让有一点微积分基础的朋友就可以弄懂。这里首先发布第一部分。由于时间匆忙等原因，可能会出现一些疏忽，欢迎大家挑错！

点击阅读全文...

其实太阳已经落到了地平线以下（大气折光）

苏剑林（BoJone） 编写/翻译

实际感受：

大家也许会有这样的生活经验：早上的太阳没有中午的太阳猛烈？从东方升起到我们的头顶，月亮一直在变“亮”？……这些现象都与地球大气的“消光”现象密切相关！

众所周知，地球有一层厚厚的大气，既是我们呼吸的来源，也是我们生命的保护伞。他为我们提供了臭氧层，也为我们提供了蓝天和风霜雨露，还为我们送上了绚丽的彩虹。然而，在天文学角度，大气却是我们的“障碍”，浓厚的大气不利于我们对宇宙进行清晰的观测。因此，天文学家们一直希望把天文台建立海拔更高的地方，因为那里有着稀薄的大气……为了渴求更高的清晰度，人们甚至把望远镜放到了地球之外。

点击阅读全文...

3月份，大地回暖，春暖花开了，精彩的天象在等着我们。这个月天空的主角无疑是美丽的土星，火星和金星也是较好的观测对象。而且3月又正值梅西叶马拉松的好时节，许多有趣、朦胧的深空天体，无疑会极大地挑起我们对神秘的春夜星空的兴趣。这里有一本《梅西叶马拉松全年指导手册》电子书，新手不妨作为入门的参考书。

梅西叶马拉松是一个自我挑战性相对较强的活动，因为虽然一夜之间所有的梅西耶天体全都亮相，但是因为升起的时间相差很多，有些天体的角度就很低了，并不十分适宜观测，况且一夜之间观测103个天体，即使对星空和器材性能非常熟悉，也需要相当时间（当然啦，你如果有电动赤道仪和导星输入的话，就很简单拉），这会是一个非常辛苦的活动，需要充分准备。 爱好挑战困难者，上吧，探索我们的宇宙！

点击阅读全文...

Solar_sys

虽然地心说早已站不住脚了，但是我们的确是站在地球上观测宇宙的，我们得把地球视为静止的，才能满足我们日常的观测所需。也就是说，必须得以地球为参照系。这样，我们其实也就重新树立了地球的“宇宙中心”地位。最典型的模型就是所谓的天球坐标系，它的本质就是把地球看做宇宙的中心...

点击阅读全文...

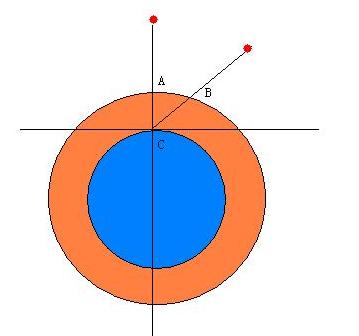
天文学中有一个名词Airmass，注意这并非Air mass（空气质量），这是指天顶距等于z的方向上大气光学厚度和天顶方向大气光学厚度之比，我目前也找不到它的中文名称究竟是什么，反正觉得如果译成“大气质量”很怪，就暂且翻译成“大气厚度指数”好了。现在知道它叫做“大气光学质量”了，一般用X表示，如下图中，$X={BC}/{AC}$。

星光传播示意图

在一片较小的区域内，大气层和地面都可以视为平行平面，这时有一个很好的近似公式：
$$X=\sec z$$
对于现在的中学教材来说，有的读者可能不了解\sec为何物，实际上：$\sec z=\frac{1}{\cos z}$

点击阅读全文...